3.哈夫曼树和哈夫曼编码

3.1带权路径长度

结点的权：有某种现实含义的数值（如：表示结点的重要性等）。

结点的带权路径长度：从树的根到该结的路径长度（经过的边数）与该结点上权值的乘积。
$$结点的带权路径长度=权\times 边数$$

比如第四层第四个结点度为3，它的带权路径长度：边数 * 权 = 3*3 = 9

树的带权路径长度（WPL, weighted path length）：树中的所有的叶子节点的带权路径长度的和。
$$WPL(树的带权路径长度)=\sum _{i=1}^n{w}_i{l}_i$$

• $w_i$是第i个叶结点所带的权值；
• $l_i$是第i个叶结点到根结点的路径长度。

3.2哈夫曼树的定义和原理

哈夫曼树（Huffman Tree）：在含有n个带权叶子节点的二叉树中，其中带权路径长度(WPL)最小的二叉树称为哈夫曼树，也称最优二叉树。

例如，在上图求WPL的四棵树中，都是4个同样权值的叶子节点，中间两棵树的WPL最小，那么它们两个就是哈夫曼树。

3.3哈夫曼树的构造

步骤：

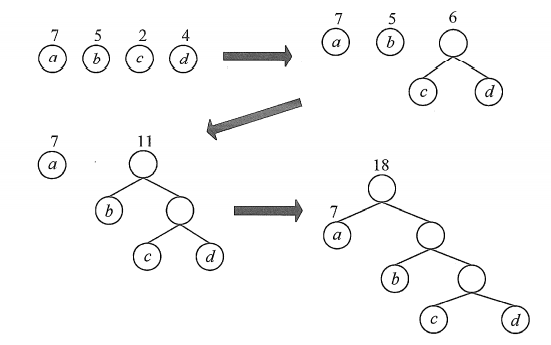
1. 先把有权值的叶子结点按照从大到小（从小到大也可以）的顺序排列成一个有序序列。
2. 取最后两个最小权值的结点作为一个新节点的两个子结点，注意相对较小的是左孩子（可以不是）。
3. 用第2步构造的新结点替掉它的两个子节点，插入有序序列中，保持从大到小排列。
4. 重复步骤2到步骤3，直到根节点出现。

看图就清晰了，如下图所示：

代码实现

typedef double DataType; //结点权值的数据类型typedef struct HTNode //单个结点的信息
{DataType weight; //权值int parent; //父节点int lc, rc; //左右孩子
}*HuffmanTree;

代码实现时，我们用一个数组（静态三叉链表）存储构建出来的哈夫曼树中各个结点的基本信息（权值、父结点、左孩子以及右孩子）。该数组的基本布局如下：

我们以“用数字7、5、4、2构建一棵哈夫曼树”为例，代码的基本实现步骤如下：

• 第一阶段

所构建的哈夫曼树的总结点个数为2 × 4 − 1 = 7，但是这里我们开辟的数组可以存储8个结点的信息，因为数组中下标为0的位置我们不存储结点信息，具体原因后面给出。

我们先将用于构建哈夫曼树的数字7、5、4、2依次赋值给数组中下标为1-4的权值位置，其余信息均初始化为0。

• 第二阶段

从数组中下标为1-4的元素中，选取权值最小，并且父结点为0（代表其还没有父结点）的两个结点，生成它们的父结点：

1、下标为5的结点的权值等于被选取的两个结点的权值之和。
 2、两个被选取的结点的父结点就是下标为5的结点。
 3、下标为5的结点左孩子是被选取的两个结点中权值较小的结点，另外一个是其右孩子。

再从数组中下标为1-5的元素中，选取权值最小，并且父结点为0的两个结点，生成它们的父结点。

继续从数组中下标为1-6的元素中，选取权值最小，并且父结点为0的两个结点，生成它们的父结点。

此时，除了下标为0的元素以外，数组中所有元素均已有了自己的结点信息，哈夫曼树已经构建完毕。

为什么数组中下标为0的元素不存储结点信息？

因为在数组中叶子结点的左右孩子是0，根结点的父结点是0，我们若是用数组中下标为0元素存储结点信息，那么我们将不能区分左右孩子为0的结点是叶子结点还是说该结点的左右孩子是下标为0的结点，同时也不知道哈夫曼树的根结点到底是谁。

// 在下标为1到i-1的范围(n个数)找到权值最小的两个值的下标, 其中s1的权值小于s2的权值, 返回s1和s2的下标
// HT是哈夫曼树的根结点，n是叶子结点的个数
void Select(HuffmanTree& HT, int n, int& s1, int& s2)
{int min;//找第一个最小值for (int i=1; i <= n; i++){if (HT[i].parent == 0){min = i;break;}}for (int i= min+1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)min = i;}s1 = min; //第一个最小值给s1//找第二个最小值for (int i=1; i <= n; i++){if (HT[i].parent == 0 && i != s1){min = i;break;}}for (int i= min+1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight && i != s1)min = i;}s2 = min; //第二个最小值给s2
}// 构建哈夫曼树
// HT是哈夫曼树的根结点，w是n个叶子结点的权值数组，n是叶子结点(初始节点)的个数
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{// step1.分配足够空间int number = 2*n - 1; //哈夫曼树总结点数HT = (HuffmanTree)calloc(number + 1, sizeof(HTNode)); //开m+1个HTNode，因为下标为0的HTNode不存储数据if (!HT){printf("分配内存失败\n");exit(0);}// step2.构建叶子结点for (int i=1; i <= n; i++){HT[i].weight = w[i - 1]; //赋权值给n个叶子结点}// step3.构建哈夫曼树(分支节点)，所以从新位置开始for (int i= n+1; i <= number; i++){//选择权值最小的s1和s2，生成它们的父结点int s1, s2;Select(HT, i-1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标，其中s1的权值小于s2的权值HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和HT[s1].parent = i; //s1的父亲是iHT[s2].parent = i; //s2的父亲是iHT[i].lc = s1; //左孩子是s1HT[i].rc = s2; //右孩子是s2}
}//打印哈夫曼树中各结点之间的关系
void PrintHuff(HuffmanTree HT, int n)
{printf("下标   权值     父结点   左孩子   右孩子\n");printf("0                                  \n");for (int i=1; i <= n; i++){printf("%-4d   %-6.2lf   %-6d   %-6d   %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);}printf("\n");
}

注：为了避免使用二级指针，函数传参使用了C++中的引用传参。

3.4特点

1. 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。

2. 哈夫曼树的结点总数为 2n - 1。

   因为共有n个叶子结点，也就是两两合成n-1次，就多了n-1个分支节点，n-1+n = 2n-1。

3. 哈夫曼树中不存在度为1的结点。

   解释度为1：就是只有一个孩子结点。

4. 哈夫曼树并不唯一，但WPL必然相同且最优。

5. 把二叉树上的所有分支都进行编号，将所有左分支都标记为0，所有右分支都标记为1。

6. 对于树上的任何一个结点，都可以根据从根结点到该结点的路径唯一确定一个编号。

【不足】当权值大小相差不大的时候，哈夫曼压缩效果不理想。

3.5哈夫曼编码

赫夫曼当前研究这种最优树的目的是为了解决当年远距离通信（主要是电报）的数据传输的最优化问题。

哈夫曼编码是一种被广泛应用而且非常有效的数据压缩编码。

比如我们有一段文字内容为“ BADCADFEED”要网络传输给别人，显然用二进制的数字(0和1)来表示是很自然的想法。我们现在这段文字只有六个字母ABCDEF，那么我们可以用相应的二进制数据表示，如下表所示：

字母	A	B	C	D	E	F
二进制字符	000	001	010	011	100	101

这样按照固定长度编码编码后就是“001000011010000011101100100011”，对方接收时可以按照3位一分来译码。如果一篇文章很长，这样的二进制串长度也将非常的可怕。

事实上，不管是英文、中文或是其他语言，字母或汉字的出现频率是不相同的。

假设六个字母的频率为A 27, B 8, C 15, D 15, E 30, F 5,合起来正好是100%。那就意味着，我们完全可以重新按照赫夫曼树来规划它们。

下图为构造赫夫曼树的过程的权值显示：

将权值左分支改为0，右分支改为1后的赫夫曼树：

这哈夫曼树的WPL为：

WPL = 2*( 15 + 27 + 30 ) + 3*15 + 4*( 5 + 8 ) = 241

此时，我们对这六个字母用其从树根到叶子所经过路径的0或1来编码，可以得到如下表所示这样的定义：

字母	A	B	C	D	E	F
二进制字符	01	1001	101	00	11	1000

---

固定长度编码：每个字符用相等长度的二进制位表示。

可变长度编码：允许对不同字符用不等长的二进制位表示。

前缀编码：若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。

由哈夫曼树得到哈夫曼编码：字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值，根据之前介绍的方法构造哈天曼树。

---

这里使用的就是可变长度编码，并且是前缀编码，这样就不会有歧义。

我们将文字内容为“ BADCADFEED”再次编码，对比可以看到结果串变小了。

原编码二进制串: 000011000011101100100011 (共 30 个字符)
新编码二进制串: 10100101010111100(共 25 个字符)

也就是说，我们的数据被压缩了，节约了大约17%的存储或传输成本。

压缩比

原本ABCDEF这6个字符，最少使用3位二进制数表示，即每个字符用3位。

通过哈夫曼树进行优化之后，按照出现频率（六个字母的频率为A 27, B 8, C 15, D 15, E 30, F 5）计算加权平均长度（字符位数）：

2*0.27 + 4*0.08 + 3*0.15 + 2*0.15 + 2*0.3 + 4*0.05 = 2.41位

【技巧】但是其实 WPL/100 就压缩后的平均位数

未压缩长度3，压缩后长度2.41，那么压缩比为：

$\frac{3-2.41}{3}\times 100\%=0.197\times 100\%=19.7\%$

代码实现

一个字符串若是想要容纳下“用n个数据生成的哈夫曼编码”中的任意一个编码，那么这个字符串的长度应该为n，因为我们还需要用一个字节的位置用于存放字符串的结束标志\0。

我们就以数字7、5、4、2构建的哈夫曼树为例，哈夫曼编码生成的基本实现步骤如下：

• 第一阶段

因为数据个数为4，所以我们开辟一个大小为4的辅助空间，并将最后一个位置赋值为\0，用于暂时存放正在生成的哈夫曼编码。

为了存放这4个数据哈夫曼编码，我们开辟一个字符指针数组，该数组中有5个元素，每个元素的类型为char**，该字符指针数组的基本布局如下：

【注意】这里为了与 “构建哈夫曼树时所生成的数组” 中的下标相对应，所以该字符指针数组中下标为0的元素也不存储有效数据。

• 第二阶段

利用已经构建好的哈夫曼树，生成这4个数据的哈夫曼编码。单个数据生成哈夫曼编码的过程如下：

1、判断该数据结点与其父结点之间的关系，若该数据结点是其父结点的左孩子，则将start指针前移，并将0填入start指向的位置，若是右孩子，则在该位置填1。

2、接着用同样的方法判断其父结点与其父结点的父结点之间的关系，直到待判断的结点为哈夫曼树的根结点为止，该结点的哈夫曼编码生成完毕。

3、将字符串中从start的位置开始的数据拷贝到字符指针数组中的相应位置。

这里我们以生成数据5的哈夫曼编码为例：

**【注意】**在每次生成数据的哈夫曼编码之前，先将start指针指向\0。

按照此方式，依次生成7、5、4、2的哈夫曼编码后，字符指针数组的基本布局如下：

哈夫曼编码生成完毕。

代码如下：

//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{HC = (HuffmanCode)malloc(sizeof(char*) * (n+1)); //开n+1个空间char**，因为下标为0的空间不用char* code = (char*)malloc(sizeof(char) * n); //辅助空间，编码最长为n(最长时，前n-1个用于存储数据，最后1个用于存放'\0')code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'for (int i = 1; i <= n; i++){int start = n - 1; //每次生成数据的哈夫曼编码之前，先将start指针指向'\0'int c = i; //正在进行的第i个数据的编码int parent_c = HT[c].parent; //找到该数据的父结点while (parent_c) //直到父结点为0，即父结点为根结点时，停止{//如果该结点是其父结点的左孩子，则编码为0，否则为1if (HT[parent_c].lc == c)code[--start] = '0';elsecode[--start] = '1';c = parent_c; //继续往上进行编码parent_c = HT[c].parent; //c的父结点}HC[i] = (char*)malloc(sizeof(char) * (n-start)); //开辟用于存储编码的内存空间strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置}free(code); //释放辅助空间
}

3.6哈夫曼树-C++

/* 二叉树哈夫曼树：在含有n个带权叶子节点的二叉树中，其中带权路径长度(WPL)最小的二叉树称为哈夫曼树，也称最优二叉树。用一个 静态三叉链表 来存储
C++实现*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>typedef double DataType; //结点权值的数据类型typedef struct HTNode //单个结点的信息
{DataType weight; //权值int parent; //父节点int lc, rc; //左右孩子
} *HuffmanTree;
typedef char **HuffmanCode;	//字符指针数组中存储的元素类型void Select(HuffmanTree& HT, int n, int& min1, int& min2);
void Select2(HuffmanTree& HT, int n, int& s1, int& s2);	//在哈夫曼树中选择两个权值最小的结点
void Select3(HuffmanTree& HT, int n, int& s1, int& s2);
void CreateHuff(HuffmanTree& HT, DataType* w, int n); //构建哈夫曼树
void PrintHuff(HuffmanTree HT, int n); //打印哈夫曼树
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n);	//哈夫曼编码double GetWpl(HuffmanTree HT, int n, int target);
double GetWPL(HuffmanTree HT, int n);
double GetAverageLength(HuffmanTree HT, HuffmanCode HC, int n);
double GetCompressionRate(HuffmanTree HT, HuffmanCode HC, int n);int main()
{//测试数据int n = 1;DataType w[] = {27,8,15,15,30,5};// 获取长度n = sizeof(w)/sizeof(DataType);//创建哈夫曼树HuffmanTree HT;CreateHuff(HT, w, n);//打印哈夫曼树PrintHuff(HT, n);HuffmanCode HC;HuffCoding(HT, HC, n);//打印哈夫曼编码for (int i=1; i <= n; i++){printf("%.2lf的哈夫曼编码是：%s\n", HT[i].weight, HC[i]);}//计算哈夫曼树的带权路径长度printf("\n哈夫曼树的带权路径长度WPL是：%.2lf\n", GetWPL(HT,n));// GetAverageLength(HC, n);printf("压缩率是 %.2lf %%", GetCompressionRate(HT, HC, n)*100);return 0;
}// ------------------------- 哈夫曼树 构建------------------------// 在下标为1到i-1的范围(n是叶子结点数)找到权值最小的两个值的下标, 其中s1的权值小于s2的权值, 返回s1和s2的下标
void Select2(HuffmanTree& HT, int n, int& s1, int& s2)
{int min;
//找第一个最小值//初始化，把第一个父结点为0的叶子结点作为最小值for (int i=1; i <= n; i++){if (HT[i].parent == 0){min = i;break;}}//在剩下的n-1个父结点为0的叶子结点中，找到权值最小的for (int i= min+1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)min = i;}s1 = min; //第一个最小值给s1//找第二个最小值for (int i=1; i <= n; i++){if (HT[i].parent == 0 && i != s1){min = i;break;}}for (int i= min+1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight && i != s1)min = i;}s2 = min; //第二个最小值给s2
}/*
设立两个变量，x(min1)，y(min2)
将数组前两个值赋值给x，y；
比对x，y的大小，
更大的值给y，更小的值给x
循环数组，与y对比，当小于y时，与x对比，若小于x，则将x的值给y，x的值为min；
大于x则将min赋值给y；
*/
void Select(HuffmanTree& HT, int n, int& min1, int& min2)
{//初始化，把第一个父结点为0的叶子结点作为最小值for (int i=1; i <= n; i++){if (HT[i].parent == 0){min1 = i;break;}}for (int i=1; i <= n; i++){if (HT[i].parent == 0 && i!=min1){min2 = i;break;}}//min1比min2小if (HT[min1].weight > HT[min2].weight){int temp = min1;min1 = min2;min2 = temp;}for (int i=1; i <= n; i++){if(HT[i].parent == 0){if (HT[i].weight < HT[min1].weight){min2 = min1;min1 = i;}else if (HT[i].weight < HT[min2].weight && i != min1){min2 = i;}}}
}void Select3(HuffmanTree& HT, int n, int& s1, int& s2)
{double min1=255, min2=255; //初始化，把第一个父结点为0的叶子结点作为最小值s1=s1=0;for (int i=1; i <= n; i++){if(HT[i].parent == 0){if (HT[i].weight < min1){min2 = min1, s2 = s1;min1 = HT[i].weight, s1 = i;}else if (HT[i].weight < min2){min2 = HT[i].weight, s2 = i;}}}
}// 构建哈夫曼树
// HT是哈夫曼树的根结点，w是n个叶子结点的权值数组，n是叶子结点(初始节点)的个数
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{// step1.分配足够空间int number = 2*n - 1; //哈夫曼树总结点数HT = (HuffmanTree)calloc(number + 1, sizeof(HTNode)); //开m+1个HTNode，因为下标为0的HTNode不存储数据if (!HT){printf("分配内存失败\n");exit(0);}// step2.构建叶子结点for (int i=1; i <= n; i++){HT[i].weight = w[i - 1]; //赋权值给n个叶子结点}// step3.构建哈夫曼树(分支节点)，所以从新位置开始for (int i= n+1; i <= number; i++){//选择权值最小的s1和s2，生成它们的父结点int s1, s2;Select(HT, i-1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标，其中s1的权值小于s2的权值HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和HT[s1].parent = i; //s1的父亲是iHT[s2].parent = i; //s2的父亲是iHT[i].lc = s1; //左孩子是s1HT[i].rc = s2; //右孩子是s2}
}//打印哈夫曼树中各结点之间的关系
void PrintHuff(HuffmanTree HT, int n)
{int m = 2*n-1;printf("哈夫曼树为:>\n");printf("下标   权值     父结点   左孩子   右孩子\n");printf("0                                  \n");for (int i=1; i <= m; i++){printf("%-4d   %-6.2lf   %-6d   %-6d   %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);}printf("\n");
}// ------------------------- 哈夫曼 编码------------------------//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{HC = (HuffmanCode)malloc(sizeof(char*) * (n+1)); //开n+1个空间char**，因为下标为0的空间不用char* code = (char*)malloc(sizeof(char) * n); //辅助空间，编码最长为n(最长时，前n-1个用于存储数据，最后1个用于存放'\0')code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'for (int i = 1; i <= n; i++){int start = n - 1; //每次生成数据的哈夫曼编码之前，先将start指针指向'\0'int c = i; //正在进行的第i个数据的编码int parent_c = HT[c].parent; //找到该数据的父结点while (parent_c) //直到父结点为0，即父结点为根结点时，停止{//如果该结点是其父结点的左孩子，则编码为0，否则为1if (HT[parent_c].lc == c)code[--start] = '0';elsecode[--start] = '1';c = parent_c; //继续往上进行编码parent_c = HT[c].parent; //c的父结点}HC[i] = (char*)malloc(sizeof(char) * (n-start)); //开辟用于存储编码的内存空间strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置}free(code); //释放辅助空间
}// --------------------------- Get -----------------------------
// 结点的带权路径长度
// 获得n个叶子情况下结点target的带权路径长度
// 结点的带权路径长度=权×边数
double GetWpl(HuffmanTree HT, int n, int target){if(target <= 0 || target > n){return -1;}int sum = 0;	//边数int parent_target = HT[target].parent;while(parent_target){sum++;parent_target = HT[parent_target].parent;}return sum * HT[target].weight;
}// 树的带权路径长度WPL
double GetWPL(HuffmanTree HT, int n){double wpl = 0;for (int i=1; i <= n; i++){wpl += GetWpl(HT, n, i);}return wpl;
}// 计算哈夫曼编码的平均长度(字符位数)
double GetAverageLength(HuffmanTree HT, HuffmanCode HC, int n){double Number_of_AVEdigits = 0;	//压缩后的平均长度(字符位数)//遍历哈夫曼编码for (int i=1; i <= n; i++){// printf("%s哈夫曼编码长度：%d\n", HC[i], strlen(HC[i]));Number_of_AVEdigits += strlen(HC[i]) * HT[i].weight / 100;}return Number_of_AVEdigits;
}// 计算压缩率
// 压缩率 = 加权平均字符位数 / 未压缩字符位数
double GetCompressionRate(HuffmanTree HT, HuffmanCode HC, int n){double Number_of_digits = 0;	//未压缩字符位数for(int i=1; i <= n; i++){if(pow(2, i) >= n){Number_of_digits = i;break;}}GetAverageLength(HT, HC, n);return (Number_of_digits - GetAverageLength(HT, HC, n) ) / Number_of_digits;
}// 计算哈夫曼编码的熵
//pase