
目录
1.粒子群算法入门
1.1 简单的优化问题
1.1.1 盲目搜索
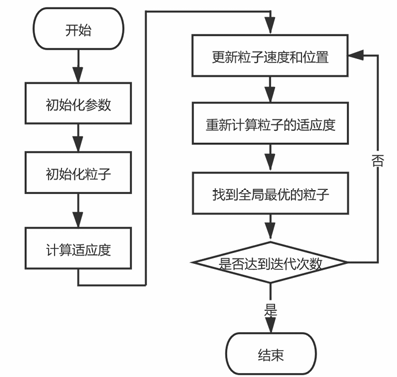
1.1.2 粒子群算法流程图
1.1.3 粒子群算法的核心公式
1.1.4 预设参数
1.1.5 初始化粒子的位置和速度
1.1.6 计算适应度
1.1.7 循环体:更新粒子速度和位置
1.1.8 模型改进
2.深入研究粒子群算法
3.粒子群算法的后续讨论
1.粒子群算法入门
在线绘图工具可以试试ProcessOn思维导图流程图-在线画思维导图流程图_在线作图实时协作
粒子群算法,全称为粒子群优化算法(Particle Swarm Optimization)。他是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的搜索算法。
这是一种启发式算法,而启发式算法的定义则是基于直观或经验构造的算法,在可接受的花费下给出待解决优化问题的一个可行解。
-
什么是可接受的花费?
计算时间和空间能接受
-
什么事优化问题?
工程设计中优化问题(optimization problem)指在一定约束条件下,求解一个目标函数的最大值或者最小值问题。
-
什么是可行?
得到的结果能用于工程实践(不一定是最优解)
常见的启发式算法,特别是在数学建模中常见给的这类算法,有粒子群、模拟退火、遗传算法、蚁群算法、禁忌搜索算法等。
1.1 简单的优化问题
目标函数:
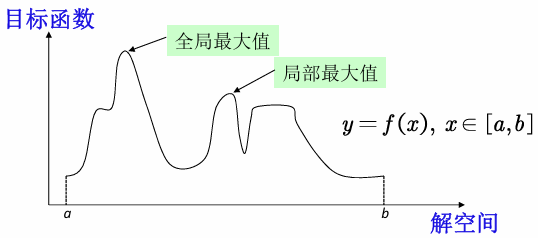
思考:怎么找到这个一元函数的最大值?(只有一个上下界约束,即函数的定义域)
盲目搜索和启发式搜索
1.1.1 盲目搜索
假设图中的a=1,b=10,我们要找出连续函数y=f(x)在[1, 10]的最大值。
(1)枚举法
如果不考虑计算时间,我们可以划分的更小,这样可以增加计算精度。
(2)蒙特卡洛模拟
随机在[a,b]区间上取N个样本点,即x1,x2,x3,…., xN都是在[a,b]取得随机数分别计算f(x1),f(x2),f(3),…,f(xN),看看其中的哪个函数值最大。
这就有很大的问题了,如果我们现在要求的是一个多变量的函数,那么要考虑的情况就会随着变量数呈指数增长,计算的时间复杂度太高啦。
所以采用启发式算法,归纳成两点:
-
任何有助于找到问题的最优解,但是不能保证找到全局最优解
-
有助于加速求解过程和找到较优解的方法。
粒子群算法的核心思想是利用群体中的个体对信息的共享使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。
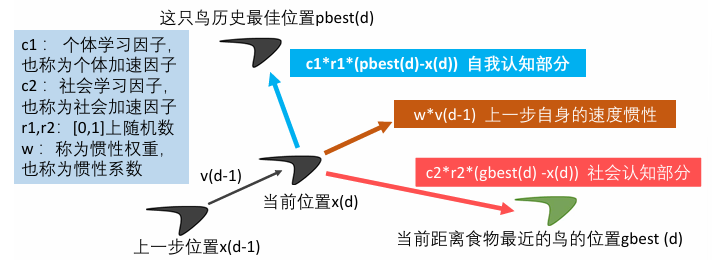
这个智能体第d步所在的位置 = 第d-1步所在的位置 + 第d - 1步的速度 * 运动的时间 x(d) = x(d - 1) + v(d - 1) * t (每一步运动的时间t一般取1)
这个智能体第d步的速度 = 上一步自身·的速度惯性 + 自我认知部分 + 社会认知部分
v(d) = w * v(d - 1) + c1 * r1 * (pbest(d) - x(d)) + c2 * r2 * (gbest(d) - x(d)) (三部分的和)
基本概念:
-
粒子:优化问题的候选解
-
位置:候选解所在的位置
-
速度:候选解移动的速度
-
适应度:评价粒子优劣的值,一般设置为目标函数值
-
个体最佳位置:单个粒子迄今为止找到的最佳位置
-
群体最佳位置:所有粒子迄今为止找的最佳位置
例题学习一下
粒子群寻找最小值ing
1.1.2 粒子群算法流程图
符号说明
| 符号 | 含义 |
|---|---|
| n | 粒子个数 |
| c1 | 粒子的个体学习因子,也称为个体加速因子 |
| c2 | 粒子的社会学习因子,也称为社会加速因子 |
| w | 速度的惯性权重 |
| vid | 第d次迭代时,第i个粒子的速度 |
| xid | 第d次迭代时,第i个粒子所在的位置 |
| f(x) | 在位置x时的适应度值(一般取目标函数值) |
| pbestid | 到第d次迭代为止,第i个粒子经过的最好的位置 |
| gbestd | 到第d次迭代为止,所有粒子经过的最好的位置 |
1.1.3 粒子群算法的核心公式
其中的r1 r2是[0, 1]上的随机数。
这里我们没有在变量说明的表格中放入r1,r2这个随机数,是因为他们博士的含义不太重要,仅做简单介绍。
1.1.4 预设参数
预设参数:学习因子
在最初提出粒子群算法的论文中指出,个体学习因子和社会(或群体)学下因子取2比较合适。(注意:最初提出粒子群算法的这篇论文没有惯性权重。
预设参数:惯性权重
论文中得到的结论:惯性权重取0.9~1.2是比较合适的,一般取0.9即可。
例1:求一元函数的最大值
在[-3,3]内的最大值
x0 = 0;
A = [];b = [];
Aeq = [];beq = [];
x_lb = -3; % x的下界
x_ub = 3; % x的上界
[x, fval] = fmincon(@Obj_fun1, x0, A, b, Aeq, beq, x_lb, x_ub)
fval = -fval
function y = Obj_fun1(x)y = -(11 * sin(x) + 7 * cos(5 * x));
end如果把初始值改为x0=2,结果会是什么?(局部最大值)
设置粒子群算法的参数
n = 10; % 粒子数量 narvs = 1; % 变量个数(函数中有几个自变量) c1 = 2; % 每个粒子的个体学习因子 c2 = 2; % 每个粒子的社会学习因子 w = 0.9; % 惯性权重 K = 50; % 迭代的次数 vmax = 1.2; % 粒子的最大速度 x_lb = -3; % x的下界 x_ub = 3; % x的上界
-
增加粒子数量会增加我们找到更好的结果的可能性,但会增加运算的时间
-
c1,c2,w这三个量有很多改进的空间
-
迭代的次数K越大越好么?不一定,当已经找到最优解,再增加迭代次数是没有意义的。
-
这里出现粒子的最大速度,是为了保证下一步的位置离当前位置不能太远,一般去自变量可行域的10%到20%(不同的文献看法不同)
-
X的下界和上界是保证粒子不会飞出定义域
1.1.5 初始化粒子的位置和速度
n = 10;
narvs = 1;
x = zeros(n, narvs);
for i = 1 : narvs% 随机初始化粒子所在的位置在定义域内x(:, i) = x_lb(i) + (x_ub(i) - x_lb(i)) * rand(n, 1);
end
% 随机初始化粒子的速度,设置为[-vmax, vmax]
v = -vmax + 2 * vmax .* rand(n, narvs);1.1.6 计算适应度
fit = zeros(n, 1); % 初始化这n个粒子的适应度全为0
for i = 1 : n % 循环整个粒子群,计算每一个粒子的适应度fit(i) = Obj_fun1(x(i, :)); % 调用Obj_fun1计算适应度
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标
gbest = x(ind, :); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)
function y = Obj_fun1(x)y = 11 * sin(x) + 7 * cos(5 * x);
end注意:
-
这里的适应度实际上就是我们的目标函数值
-
这里可以直接计算出pbest和gbest,在后面将用于计算粒子的速度以更新粒子的位置。
1.1.7 循环体:更新粒子速度和位置
for d = 1 : K % 开始迭代,一共迭代K次 for i = 1 : n % 依次更新第i个粒子的速度与位置% 更新第i个粒子的速度v(i, :) = w * v(i, :) + c1 * rand(1) * (pbest(i, :) - x(i, :)) + c2 * rand(1) * (gbest - x(i, :));% 如果粒子的速度超过最大速度限制,就对其进行调整for j = 1 : narvsif v(i,j) < -vmax;v(i, j) = -vmax(j);elseif v(i, j) > vmax(j);v(i, j) = vmax(j);endendx(i, :) = x(i, :) + v(i, :); % 更新第i个粒子的位置% 如果粒子的位置超出了定义域,就对其进行调整for j = i : narvsif x(i, j) < x_lb(j)x(i, j) = x_lb(j);elseif x(i, j) > x_ub(j)x(i, j) = x_ub(j);endendfit(i) = Obj_fun1(x(i, :)); % 重新计算第i个粒子的适应度% 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度if fit(i) > Obj_fun1(pbest(i, :))pbest(i, :) = x(i, :); % 那就更新第i个粒子迄今为止找到的最佳位置end% 如果第i个粒子的适应度大于所有粒子的迄今为止找到的最佳位置对应的适应度if Obj_fun1(pbest(i, :)) > Obj_fun1(gbest)gbest = pbest(i, :); % 那就更新所有粒子迄今为止找到的最佳位置endend
end粒子群算法运行的结果
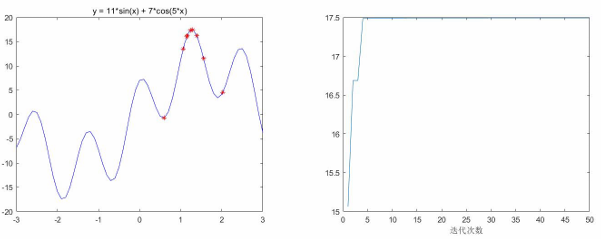
n = 10; % 粒子数量 c1 = 2; % 每个粒子的个体学习因子 c2 = 2; % 每个粒子的社会学习因子 w = 0.9; % 惯性权重 K = 50; % 迭代次数
例2:求二元函数的最小值
求函数
在x1,x2∈[-15, 15]内的最小值
注意:用粒子群算法求解函数最小值时,粒子适应度的计算我们仍设置为目标函数值,但是此时我们希望找到适应度最小的解,因此为了避免混淆可以直接用目标函数值来代替适应度的说法。
绘制立体图显示:
% 定义x1和x2的范围
x1 = linspace(-15, 15, 100);
x2 = linspace(-15, 15, 100);
% 创建网格
[X1, X2] = meshgrid(x1, x2);
% 定义函数 y
Y = X1.^2 + X2.^2 - X1.*X2 - 10*X1 - 4*X2 + 60;
% 绘制立体图
figure
surf(X1, X2, Y);
% 添加图形标签和轴标签
xlabel('x1');
ylabel('x2');
zlabel('y');
% 调整视角
view(45, 30);
% 添加颜色栏以展示不同的高度
colorbar;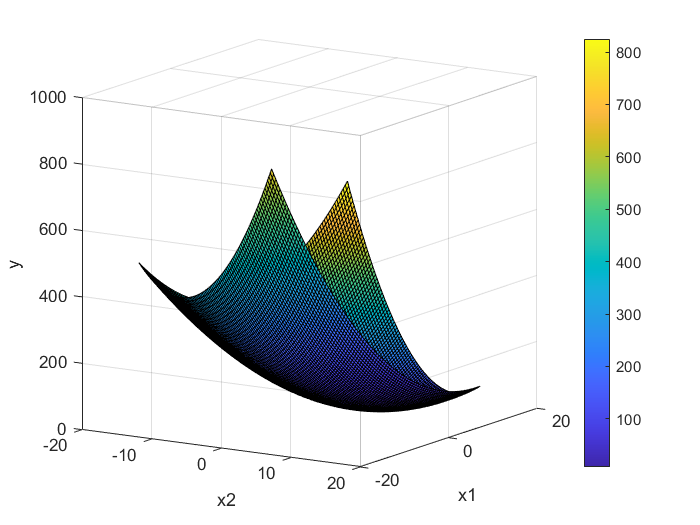
%% 粒子群算法PSO:求解函数y = x1^2 + x2^2 - x1*x2 - 10*x1 -4*x2 + 60
clear; clc;
% 绘制函数的图形
x1 = -15 : 0.1 : 15;
x2 = -15 : 0.1 : 15;
[x1, x2] = meshgrid(x1, x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2, y);
xlabel('x1'); ylabel('x2');zlabel('y');
axis vis3d % 冻结屏幕高宽比,使得三维对象的旋转不会发生坐标轴的刻度显示
hold on
% 粒子群算法中的预设参数(参数设置不是固定的,可以适当修改)
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2; % 每个粒子的个体学习因子
c2 = 2; % 每个粒子的社会学习因子
w = 0.9; % 惯性权重
K = 100; % 迭代次数
vmax = [6, 6]; % 粒子的最大速度
x_lb = [-15, -15]; % x的下界
x_ub = [15, 15]; % x的上界
% 初始化粒子的位置和速度
x = zeros(n, narvs);
for i = 1 : narvsx(:, i) = x_lb(i) + (x_ub(i) - x_lb(i)) * rand(n, 1); % 随机初始化粒子所在位置在定义域内
end
v= -vmax + 2 * vmax .* rand(n, narvs); % 随机初始化粒子的速度
% 计算适应度(注意,因为是最小化问题,所以适应度越小越好)
fit = zeros(n, 1); % 初始化这n个粒子的适应度全为0
for i = 1 : nfit(i) = Obj_fun2(x(i, :)); % 找打适应度最小的粒子的下标
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置
ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标
gbest = x(ind, :); % 定义所有粒子迄今为止找到的最佳位置
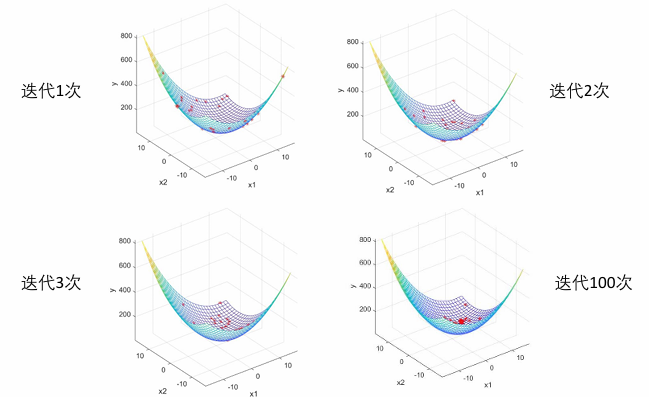
% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:, 1), x(:, 2), fit, '*r'); % scatter3是绘制三维散点图的函数
% 迭代K次来更新速度与位置
fitnessbest = ones(K, 1); % 初始化每次迭代得到的最佳的适应度
for d = 1 : K; % 开始迭代,一个迭代K次for i = 1 : n % 依次更新第i个粒子的速度与位置v(i, :) = w * v(i, :) + c1 * rand(1) * (pbest(i, :) - x(i, :)) + c2 * rand(1) * (gbest - x(i, :)); % 更新第i个粒子的速度% 如果粒子超过了最大速度的限制,就对其进行调整for j = 1 : narvsif v(i, j) < -vmax(j)v(i, j) = -vmax(j);elseif v(i, j) > vmax(j)v(i, j) = vmax(j);endendx(i, :) = x(i, :) + v(i, :); % 更新第i个粒子的位置% 如果粒子的位置超出了定义域,就对其进行调整for j = 1 : narvsif x(i, j) < x_lb(j)x(i, j) = x_lb(j);elseif x(i, j) > x_ub(j)x(i, j) = x_ub(j);endendfit(i) = Obj_fun2(x(i, :)); % 重新计算第i个粒子的适应度if fit(i) < Obj_fun2(pbest(i, :))pbest(i, :) = x(i, :); % 一直更新到第i个粒子迄今为止找到的最佳位置endif fit(i) < Obj_fun2(gbest)gbest = pbest(i, :);endendfitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳适应度pause(0.1); % 暂停0.1秒h.XData = x(:, 1); % 更新散点图句柄的x轴的数据h.YData = x(:, 2); % 更新散点图句柄的y轴的数据h.ZData = fit; % 更新散点图句柄的z轴的数据
end
figure(2)
plot(fitnessbest); % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳位置是'); disp(gbest)
disp('此时最优值是'); disp(Obj_fun2(gbest))1.1.8 模型改进
改进:线性递减惯性权重
惯性权重w体现的是粒子继承先前的速度的能力,Shi.Y最先将惯性权重w引入到粒子群算法中,并分析指出一个较大的惯性权值有利于全局搜索,而一个比较小的权值则更有利于局部搜索。wield更好地平衡算法的全局搜索以及局部搜素能力,Shi.Y提出了线性递减惯性权重LDIW(linear Decreasing Inertia Weight)
d是当前迭代的次数,K是迭代总次数
wstart一般取0.9,wend一般取0.4
原来的相比,现在惯性权重和迭代次数有关
拓展:非线性递减惯性权重
三种递减权重的图形
w_start = 0.9; w_end = 0.4;
K = 30; d = 1 : K;
w1 = w_start - (w_start - w_end) * d / K;
w2 = w_start - (w_start - w_end) * (d / K).^2;
w3 = w_start - (w_start - w_end) * (2 * d / K - (d / K).^2);
plot(d, w1, 'r', w2, 'b', w3, 'g');
legend('w1', 'w2', 'w3')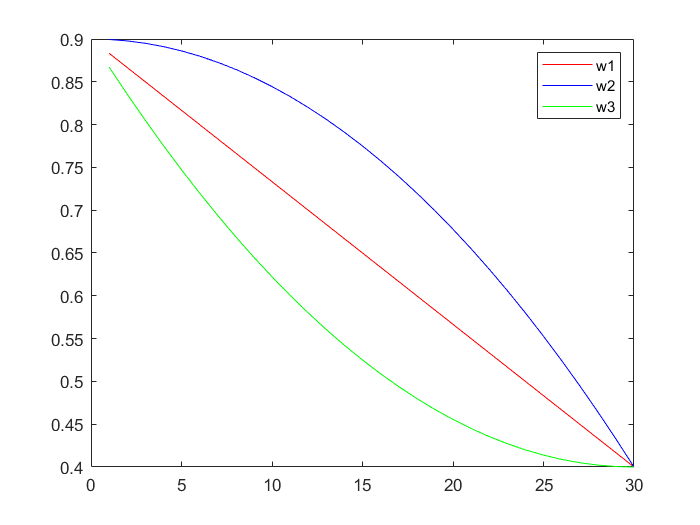
改进:自适应惯性权重
假设现在求最小值问题,那么
-
其中wmin和wmax使我们预先给定的最小惯性系数和最大惯性系数,一般取0.4和0.9
-
faveraged为f(xid)/n的总和,即第d次迭代时所有离子的平均适应度
-
fmind则是找出第d次迭代中所有粒子的最小适应度
改进:自适应惯性权重
假设现在求解的是最大值问题,那么就是上一问的表达式的相反形式
一个较大的惯性权值有利于全局搜索
而一个较小的权值则更有利于局部搜索
假设现在一共有五个粒子ABCDE,他们的适应度分别为1,2,3,4,5,取最大惯性权重为0.9,最小权重为0.4,那么这屋额个离子的惯性权重应该为0.9,0.9,0.9,0.65,0.4
适应度越小,说明距离最优解越远,此时更需要全局搜索
适应度越大,说明距离最优解越近,此时更需要局部搜素
改进:随机惯性权重
使用随机的惯性权重,可以避免在迭代前期局部搜索能力的不足,也可以避免在迭代后期全局搜索能力的不足。
改进:随机惯性权重
参考文献:基于随机惯性权重的简化粒子群优化算法
这里的σ表示的是标准差,一般取0.2~0.5之间的一个数
改进:压缩(收缩)因子法
个体学习因子c1和社会学习因子c2决定了粒子本身经验信息和其他粒子的经验信息对粒子的运动轨迹的影响,反应了粒子群之间的信息交流。设置c1较大的值,会使粒子过多地在自身的局部范围内搜索,而较大的c2的值,则有会促使粒子过早收敛到局部最优值。
为了有效地控制粒子的飞行速度,使算法达到全局搜索和局部搜索两者之间的有效平衡。Clerc构造了引入收缩因子的PSO模型,采用压缩因子,这种调整方式通过合适选取参数,可以确保PSO算法的收敛性,并可取消对速度的边界限制。
在压缩因子法中应用较多的个体学习因子c1和社会学习因子c2均取2.05,用我们的符号可以表示

改进:非对称学习因子

c1_ini = 2.5; % 个体学习因子的初始值
c1_fin = 0.5; % 个体学习因子的最终值
c2_ini = 1; % 社会学习因子的初始值
c2_fin = 2.25; % 社会学习因子的最终值
...
for d = 1 : Kc1 = c1_ini + (c1_fin - c1_ini) * d / K;c2 = c2_ini
...优化问题的测试函数

改进:自动退出迭代循环
当粒子已经找到最佳位置后,在增加迭代次数只会浪费计算时间,那么我们能否设计一个策略,能够自动退出迭代呢?
-
初始化最大的迭代次数、计数器以及最大值
-
定义函数变化量的容忍度,一般取非常小的正数
-
在迭代的过程中,每次计算出来的最佳适应度后,都计算该适应度和上次迭代时最佳适应度的变化值(取绝对值)
-
判断这个变化量和函数变换量容忍度的相对大小,如果前这小,则计数器+1,否则计数器清零
-
不断重复这个过程,有以下两种可能:
-
此时还没有超过最大的迭代次数,计数器的值超过了最大计数值,那么跳出迭代循环,搜索结束
-
此时已经达到了最大迭代次数,阿么直接跳出循环,搜索结束。
-
2.深入研究粒子群算法
particleswarm——Matlab自带的这个函数优化的特别好,运行速度快且找到的解也比较精准,但是内部的实现比较复杂,后面我们会简单介绍这个函数的实现思路。(代码如何跑得快:少些循环和判断语句,多基于矩阵运算来进行操作)
下面我们用Matlab这个内置函数粒子群函数来演示如何求解Rosenbrock函数的最小值
注意:
-
这个函数在R2014b版本以后推出
-
这个函数式求最小值的,如果目标函数求最大值则需要添加符号从而转换为求最小值
Matlab粒子群函数的细节讲解
Matlab中particlaswarm函数采用的是自适应的邻域模式
预设参数的选取
-
粒子个数swarmSize 默认设置为:min{100, 10 * narvs},narvs是变量个数
-
惯性权重InertiaRange 默认设置的范围为[0.1, 1.1],注意,,在迭代过程中惯性权重会采取自适应措施,随着迭代过程不断调整。
-
个体学习因子SelfAdjustmenWeight 默认值设置为:1.49(和压缩因子的系数几乎相同)
-
社会学习因子 SocialAdjustmentWeight 设置为:1.49(和压缩因子的系数几乎相同)
-
邻域内离子的比例MinNeighborsFraction 默认设置为0.25,由于采取的是邻域模式,因此定义了一个邻域最少粒子数目,minNeighborhoodSize = max[2, (粒子数目*邻域内粒子的比例)的整数部分]在迭代开始后,每个粒子会有一个邻域,初始时候邻域内的粒子个数(记为Q)就等于邻域最少粒子数目,后续邻域内的粒子个数Q会自适应调整。
变量初始化和适应度的计算
-
速度初始化:和我们之前的类似,只不过最大速度就是上下界之间的差额
-
位置初始化:和我们之前的类似
-
计算每个粒子的适应度:仍然设置为我们要优化的目标函数,由于该函数求解的是最小问题,因此,最优解应当为适应度最小即函数越小的解
-
初始化个体最优位置
-
初始化所有粒子的最优位置
更新粒子的速度和位置
-
随机生成粒子i的邻域,邻域内一共Q个粒子(包含粒子i本身),并找到这Q个位置最佳的那个粒子,此时它的目标函数值最小,记录位置lbest
-
更新粒子i的速度,公式已经写了很多遍了,这里不做过多赘述。这个速度公式和基本粒子群算法最大的不同就是这里的群体信息交流部分使用的是邻域内最优位置,而不是整个粒子群的最优位置;
-
更新粒子i的位置,与基本算法一致
-
修正位置和速度:若粒子i的位置超过了约束,就将其位置修改到边界处;另外如果这个粒子的位置在边界处,我们还需要查看其速度是否超过了最大速度,如果超过的话这个速度变为0(注意:如果是多元函数的话可能只有在某个分量超过了约束,我们的修改只需要针对这个分量即可)
-
计算粒子i的适应度,若小于其历史最佳的适应度,就更新粒子i的历史最佳位置现在的位置;另外还需要判断粒子i的适应度是否要小于所有粒子迄今为止找到的最小的适应度,如果小的话需要更新所有的粒子的最佳位置为粒子i的位置。
自适应调整参数
假设在第d次迭代过程中,所有的粒子的信息都已经更新好了,那么在开始下一次迭代之前,需要更新模型中的参数,这里就体现了自适应过程。
规则如下:计此时所有粒子的最小适应度为a,上一次迭代完成后所有粒子的最小适应度为b,比较a和b的相对大小,若a<b则flag=1,else flag = 0
若flag = 0,那么采取如下操作
-
更新c = c + 1;这里的c表示停止次数计数器,在迭代开始前初始化为0
-
更新Q = min{Q + minNeighborhoodSize, SwarmSize};Q:邻域内的粒子个数
若flag = 1,那么采取如下操作
-
更新Q=minNeighborhoodSize
-
更新c=max{c-1, 0}
-
判断c的大小,如果c<2,则更新w=2*w;若c>5,则更新w=w/2;这里的w是惯性权重,若计算的结果超过了惯性权重的上界或低于下界都需要将其进行调整到边界处
自适应体现在:如果适应度开始停滞时,粒子群搜索会从邻域模式向全局模式转换,一旦适应度开始下降,则会恢复到局部最优。当适应度的停滞次数足够大时。惯性系数开始逐渐变小,从而利益局部搜索。
自动退出迭代循环
Matlab自带的粒子群函数可以设置几种自动退出迭代循环的方法。

修改函数的参数
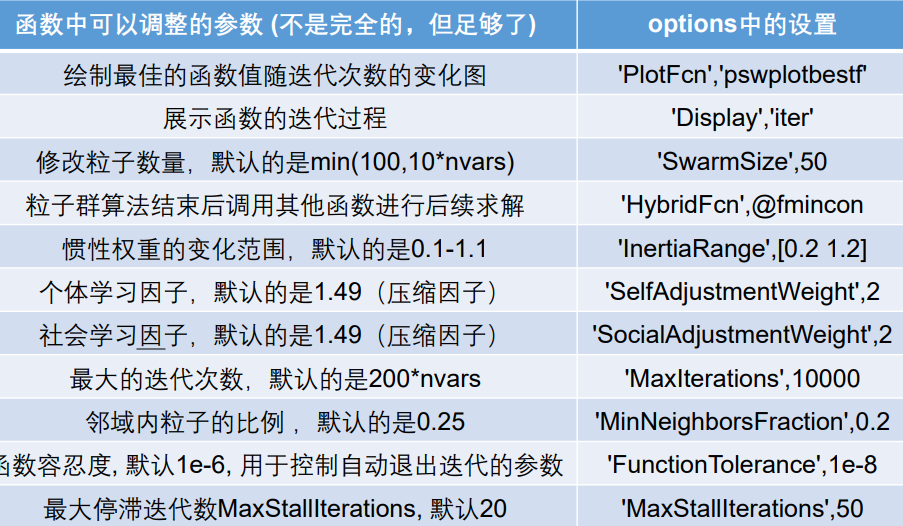
参考:matlab官网关于粒子群算法函数的说明
当然我们也可以从粒子群技术调用其他函数进行混合求解,这个我调试过,结果可能正如粒子群结果小范围波动,也有比较离谱的,不太符合的情况出现。
3.粒子群算法的后续讨论
-
粒子群算法可以解决非线性约束问题吗?
当然是可以的啦,数模中有很多题目求解的是多目标优化模型,常涉及到非线性方程。在适应度函数上构造惩罚项,对违反约束的情况进行惩罚,将有约束的优化问题转化为无约束的优化问题。
-
粒子群算法可以解决组合优化问题吗》
优化问题可以分为两类:一类是具有连续型的变量,例如我们之前探讨的求解函数极值的问题,称为连续优化问题;另一类是具有离散型的变量,例如0-1规划问题,TSP旅行商问题,成为哦组合优化问题。
解决思路:1.对原来粒子群算法的运动公式和运算符号进行重新定义 2.利用其他的只能算法和粒子群算法结合,进行混合求解。
这类问题后面有更好的解决办法:模拟退火

















![[C++] 深入理解面向对象编程特性 : 继承](https://img-blog.csdnimg.cn/img_convert/586d513c4cf14a2316b9524419de0f98.png)
