双指针
在处理数组和链表相关问题时,双指针技巧是经常用到的,双指针技巧主要分为两类:左右指针和快慢指针。所谓左右指针,就是两个指针相向而行或者相背而行;而所谓快慢指针,就是两个指针同向而行,一快一慢。
15. 三数之和(⭐️⭐️)
思路
两数之和 -> 三数之和 -> N 数之和
代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;public class ThreeSumTarget {public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(nums);for (int i = 0; i < nums.length; i++) {if (nums[i] > 0) {return res;}if (i > 0 && nums[i] == nums[i - 1]) {continue;}int left = i + 1;int right = nums.length - 1;while (left < right) {int sum = nums[i] + nums[left] + nums[right];if (sum < 0) {left++;} else if (sum > 0) {right--;} else {res.add(Arrays.asList(nums[i], nums[left], nums[right]));while ((left < right) && (nums[right] == nums[right - 1])) {right--;}while ((left < right) && nums[left] == nums[left + 1]) {left++;}right--;left++}}}return res;}}
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;public class NSumTarget {public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);return nSumTarget(nums, 3, 0, 0);}private List<List<Integer>> nSumTarget(int[] nums, int n, int start, int target) {int size = nums.length;List<List<Integer>> res = new ArrayList<>();if (n < 2 || size < n) {return res;}if (n == 2) {int low = start;int high = size - 1;while (low < high) {int sum = nums[low] + nums[high];int left = nums[low];int right = nums[high];if (sum < target) {while (low < high && nums[low] == left) {low++;}} else if (sum > target) {while (low < high && nums[high] == right) {high--;}} else {res.add(new ArrayList<>(Arrays.asList(left, right)));while (low < high && nums[low] == left) {low++;}while (low < high && nums[high] == right) {high--;}}}} else {for (int i = start; i < size; i++) {if (i > start && nums[i] == nums[i - 1]) {continue;}List<List<Integer>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);for (List<Integer> arr : sub) {arr.add(nums[i]);res.add(arr);}while (i < size - 1 && nums[i] == nums[i + 1]) {i++;}}}return res;}}复杂度
- 时间复杂度:O(N^2)
- 空间复杂度:O(logN)
5. 最长回文子串(⭐️⭐)
思路
寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串,对于最长回文子串,就是这个意思:
for 0 <= i < len(s):找到以 s[i] 为中心的回文串更新答案找回文串的关键技巧是传入两个指针 left 和 right 向两边扩散,因为这样实现可以同时处理回文串长度为奇数和偶数的情况。
for 0 <= i < len(s):# 找到以 s[i] 为中心的回文串palindrome(s, i, i)# 找到以 s[i] 和 s[i+1] 为中心的回文串palindrome(s, i, i + 1)更新答案代码
public class LongestPalindromicSubstring {public String longestPalindrome(String s) {String res = "";for (int i = 0; i < s.length(); i++) {String s1 = palindrome(s, i, i); // 奇数情况String s2 = palindrome(s, i, i + 1); // 偶数情况res = res.length() > s1.length() ? res : s1;res = res.length() > s2.length() ? res : s2;}return res;}private String palindrome(String s, int left, int right) {while (left >= 0 && right < s.length()&& s.charAt(left) == s.charAt(right)) {left--;right++;}return s.substring(left + 1, right);}}复杂度
- 时间复杂度:O(N^2)
- 空间复杂度:O(N)
88. 合并两个有序数组(⭐️⭐️)
思路
代码
public class MergeTwoArray {// 双指针public void merge1(int[] nums1, int m, int[] nums2, int n) {int p1 = 0;int p2 = 0;int[] sorted = new int[m + n];int cur = 0;int i = 0;while (p1 < m && p2 < n) {if (nums1[p1] < nums2[p2]) {sorted[i++] = nums1[p1++];} else {sorted[i++] = nums2[p2++];}}while (p1 < m) {sorted[i++] = nums1[p1++];}while (p2 < n) {sorted[i++] = nums2[p2++];}for (i = 0; i < m + n; i++) {nums1[i] = sorted[i];}}// 逆向双指针public void merge2(int[] nums1, int m, int[] nums2, int n) {int i = m - 1;int j = n - 1;int p = nums1.length - 1;while (i >= 0 && j >= 0) {if (nums1[i] > nums2[j]) {nums1[p] = nums1[i];i--;} else {nums1[p] = nums2[j];j--;}p--;}while ( j>= 0) {nums1[p] = nums2[j];j--;p--;}}}复杂度
- 时间复杂度:O(N)
- 空间复杂度:双指针:O(N),逆向双指针:O(1)
二分查找
int binarySearch(int[] nums, int target) {int left = 0, right = nums.length - 1; while(left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1; } else if(nums[mid] == target) {// 直接返回return mid;}}// 直接返回return -1;
}33. 搜索旋转排序数组(⭐️⭐️)
思路
代码
public class SearchInRotatedSortedArray {/*nums = [4,5,6,7,0,1,2]例如 target = 5, 目标值在左半段,因此在 [4, 5, 6, 7, inf, inf, inf] 这个有序数组里找就行了例如 target = 1, 目标值在右半段,因此在 [-inf, -inf, -inf, -inf, 0, 1, 2] 这个有序数组里找就行了*/public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {return mid;}if (target >= nums[0]) {if (nums[mid] < nums[0]) {nums[mid] = Integer.MAX_VALUE;}} else {if (nums[mid] >= nums[0]) {nums[mid] = Integer.MIN_VALUE;}}if (nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;}}复杂度
- 时间复杂度:O(logN)
- 空间复杂度:O(1)
69. x 的平方根(⭐️⭐️)
思路
代码
public class Sqrt {public int mySqrt(int x) {int left = 0, right = x, res = -1;while (left <= right) {int mid = left + (right - left) / 2;if ((long) mid * mid <= x) {res = mid;left = mid + 1;} else {right = mid - 1;}}return res;}}复杂度
- 时间复杂度:O(N)
- 空间复杂度:O(1)
240. 搜索二维矩阵 II(⭐️)
思路
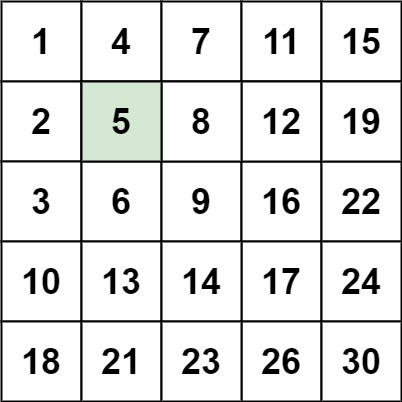
代码
public class SearchMatrix {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int i = 0, j = n - 1;while (i < m && j >= 0) {if (matrix[i][j] == target) {return true;}if (matrix[i][j] < target) {i++; // 需要大一点,往下移动} else {j--; // 需要小一点,往左移动}}return false;}}复杂度
- 时间复杂度:O(M + N)
- 空间复杂度:O(1)
34. 在排序数组中查找元素的第一个和最后一个位置(⭐️)
思路
代码
public class SearchRange {public int[] searchRange(int[] nums, int target) {return new int[]{leftRange(nums, target), rightRange(nums, target)};}private int leftRange(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {right = mid - 1;}}if (left < 0 || left >= nums.length) {return -1;}return nums[left] == target ? left : -1;}private int rightRange(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {left = mid + 1;}}if (right < 0 || right >= nums.length) {return -1;}return nums[right] == target ? right : -1;}}复杂度
- 时间复杂度:O(log(N))
- 空间复杂度:O(1)
34. 在排序数组中查找元素的第一个和最后一个位置(⭐️)
思路
代码
class Solution {public int[] searchRange(int[] nums, int target) {return new int[]{leftBound(nums, target), rightBound(nums, target)};}private int leftBound(int[] nums, int target) {int left = 0, right = nums.length - 1;// 搜索区间为 [left, right]while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {// 搜索区间变为 [mid+1, right]left = mid + 1;} else if (nums[mid] > target) {// 搜索区间变为 [left, mid-1]right = mid - 1;} else if (nums[mid] == target) {// 收缩右侧边界right = mid - 1;}}// 检查出界情况if (left >= nums.length || nums[left] != target) {return -1;}return left;}private int rightBound(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 这里改成收缩左侧边界即可left = mid + 1;}}// 这里改为检查 right 越界的情况,见下图if (right < 0 || nums[right] != target) {return -1;}return right;}}复杂度
- 时间复杂度:O(log(N))
- 空间复杂度:O(N)
162. 寻找峰值(⭐️)
思路
代码
public class FindPeakElement {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > nums[mid + 1]) {right = mid;} else {left = mid + 1;}}return left;}}复杂度
- 时间复杂度:O(logN)
- 空间复杂度:O(1)
位运算
136. 只出现一次的数字(⭐️)
思路
代码
public class SingleNumber {public int singleNumber(int[] nums) {int res = 0;for (int n : nums) {res ^= n;}return res;}}复杂度
- 时间复杂度:O(N)
- 空间复杂度:O(1)


















