替代 SMR 算法！两步孟德尔随机化方法 TWMR 与 revTWMR 整合xQTL+GWAS数据分析基因表达与疾病的关联

全基因组关联研究（GWAS）是研究大型队列中基因型与表型关系的重要工具。GWAS的已知局限性主要在于从与致病变异相关的连锁不平衡区域中识别生物学机制，而无法直接获得基因层面的表型关联。为了解决这个问题，基于转录组关联研究（TWAS）的替代方法专注于使用基因表达揭示基因与性状之间的联系。尽管对于拥有基因型、转录组学和表型数据的大型队列，可以应用两阶段最小二乘回归，但这种方法仍然存在一些问题：

i）建立这样的队列成本很高；
ii）从回归分析中提取基因与性状之间的因果方向并不直接。

为克服这些问题，Porcu等人提出了一种两步孟德尔随机化方法 TWMR，该方法利用GWAS汇总统计数据和公开的eQTL数据关联基因型和基因表达，属于孟德尔随机化方法系列。简而言之，TWMR将遗传变异作为工具变量，基因表达作为暴露变量，感兴趣的性状作为结果。在此基础上，Porcu等人还提出了一种TWMR方法的反向版本revTWMR。值得注意的是，将eQTL替换为其它类型的xQTL数据，TWMR系列方法还可用于探索其他组学（如蛋白组学和甲基组学）的因果效应。

▲ 上文为Porcu等人开发的方法revTWMR，于21年发表于NC。最早的TWMR方法也于2019年发表在该杂志。

为了加速TWMR和revTWMR的使用，来自瑞士洛桑大学的研究者开发了一款优化的、更快速的Python库pyTWMR，于2024年8月10日发表在 Bioinformatics [IF=4.4] 上。pyTWMR在支持GPU运算的前提下整合了TWMR于revTWMR流程，在处理高度相关的遗传变异和基因表达时更加稳健。

▲ DOI: 10.1093/bioinformatics/btae505

本文主要介绍pyTWMR的使用示例，代码及相关文件在后台回复 pyTWMR 即可获得。感兴趣的铁子可以自行在下方网址了解更多信息：

https://github.com/soreshkov/pyTWMR/tree/master

1 pyTWMR的安装

在.ipynb文件或命令行下运行以下代码进行安装：

%%bash
pip3 install git+https://github.com/soreshkov/pyTWMR.git

如果网络不好，推荐进行本地安装(需要移动到pyTWMR-master文件夹所在路径):

%%bash
# python版本大于3.10，可以运行成功
pip install ./pyTWMR-master/

小编是在linux下配置环境，在window尝试配置环境时请修改上方bash为cmd。

2 导入所需的库

运行以下代码导入一些所需的库(需要提前安装)：

from TWMR import TWMR
from revTWMR import revTWMR
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')

3 TWAS分析

① TWAS分析的输入是GWAS和eQTL数据，使用下方代码读入示例数据：

effect = pd.read_csv('data/TWMR/ENSG00000000419.matrix', sep='\t', index_col=0)
effect.head()

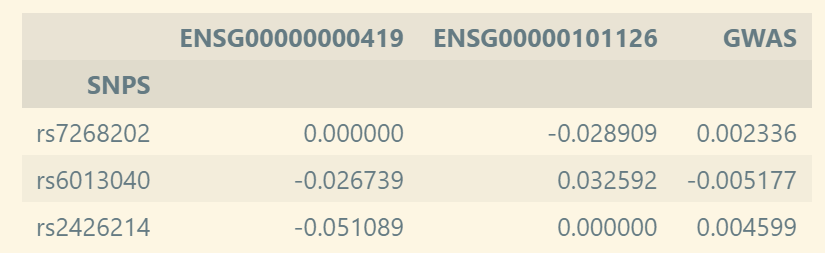
▲ 代码中effect表介绍：每一行代表一个 SNP；每一列代表一个基因，对应填充值为 QTL 结果中 SNP 对基因表达的效应，最后一列为 GWAS 结果中每个 SNP 对所研究性状的效应。

此外，还需要effect表中所有SNP之间的LD相关矩阵，上方总共三个SNP，所以矩阵形状为3*3：

ld = pd.read_csv('data/TWMR/ENSG00000000419.ld', sep='\t', header=None).to_numpy().astype(np.float32)
ld
#array([[1.       , 0.0487694, 0.151668 ],
#       [0.0487694, 1.       , 0.118453 ],
#       [0.151668 , 0.118453 , 1.       ]], dtype=float32)

② 执行TWMR分析，将结果整合成一个表格：

nGWAS = 239087 # 设置GWAS研究的样本数
nQTLs = 32000 # 设置QTLs研究的样本数
result = TWMR(beta=effect.drop('GWAS', axis=1).to_numpy(), gamma=effect['GWAS'].to_numpy(), nEQTLs=nQTLs, NGwas=nGWAS, ldMatrix=ld, pseudoInverse=False, device='cpu')
result_df = pd.DataFrame()
result_df['Gene'] = effect.columns.drop('GWAS')
result_df['Alpha'] = result.Alpha
result_df['Standard error'] = result.Se
result_df['p-value'] = result.Pval
result_df['Heterogenity p-value'] = result.HetP
display(result_df)
# Gene Alpha Standard error p-value Heterogenity p-value
#0 ENSG00000000419 -0.005793 0.006057 0.338818 1.0
#1 ENSG00000101126 -0.013730 0.005323 0.009903 1.0

结果表格的表头解释可以参照官方的说明：

Alpha: Causal effect estimated by TWMR.
Se: Standard error of Alpha.
Pval: P-value calculated from Alpha and Se.
D: Cohrian Q statistics for QTLs.
HetP: P-value for heterogeneity test.

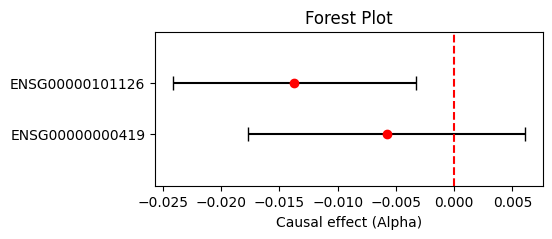
③ 森林图可视化TWMR结果:

# 计算置信区间
result_df['CI_lower'] = result_df['Alpha'] - 1.96 * result_df['Standard error']
result_df['CI_upper'] = result_df['Alpha'] + 1.96 * result_df['Standard error']# 森林图可视化
fig, ax = plt.subplots(figsize=(5, 2))
y_positions = [yi+1 for yi in range(len(result_df))]
plt.errorbar(result_df['Alpha'], y_positions,xerr=[result_df['Alpha'] - result_df['CI_lower'], result_df['CI_upper'] - result_df['Alpha']],fmt='o', color='red', ecolor='black', capsize=5)
plt.yticks(y_positions, result_df['Gene'])
plt.ylim(0, max(range(len(result_df['Gene'])))+2)
plt.axvline(x=0, linestyle='--', color='red')plt.xlabel('Causal effect (Alpha)')
plt.title('Forest Plot')
plt.show()

3 RevTWMR 分析

① RevTWMR分析的输入有所差异，但同样也是来自GWAS于eQTL数据：

effect = pd.read_csv("data/revTWMR/effect.matrix.tsv", sep='\t', index_col=0)
effect.iloc[0:5, -5:]# sample_size
gwasEffect = effect.BETA_GWAS.values
nGwas = effect.N.values
sample_size = pd.read_csv("data/revTWMR/genes.N.tsv", sep='\t', index_col=0).N.to_dict()
sample_size
#{'ENSG00000000003': 9047.50387596899,
# 'ENSG00000000419': 30201.3203125,
#...
# 'ENSG00000070759': 30987.2519685039,
# 'ENSG00000070761': 30780.3671875,
# ...}

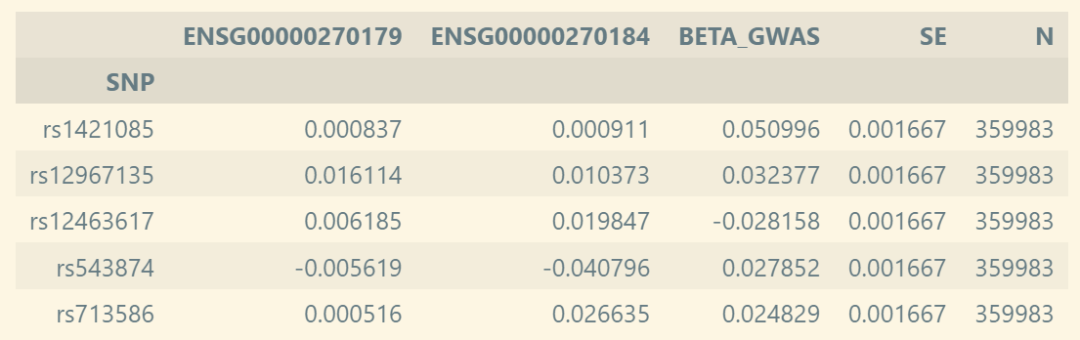
▲ 代码中effect表的介绍：每一行代表一个 SNP；每一列代表一个基因，对应填充值为 QTL 结果中 SNP 对基因表达的效应。和 TWMR 不一样的地方在于，需要将在 TWMR 输入表中的最后一列 GWAS 改名为 BETA_GWAS，同时补充标准误 SE 与研究样本数 N。

此外，还需要提供基因的sample_size文件，描述为每个基因对应的QTL Exposure sample size:

standardized study size for each gene

② 执行RevTWMR分析，将结果整合成一个表格：

results = {}
# 注意示例代码下方的循环只分析了前 5 个基因
for gene in effect.drop(['BETA_GWAS', 'SE', 'N'], axis=1).columns[:5]:    effectTbl = effect.drop(['BETA_GWAS', 'SE', 'N'], axis=1)[gene].valuesnQtls = sample_size[gene]result = revTWMR(effectTbl, gwasEffect, qtlLabels=effect.index.values, gwasSizes=nGwas, qtlExpSize=nQtls,pValIterativeThreshold=0.05, pseudoInverse=False, device='cpu')results[gene] = {'Alpha Original': result.Alpha,'SE Original': result.Se,'P Value Original': result.Pval,'N Original': result.N,'P heterogeneity Original': result.HetP,'Alpha': result.AlphaIterative,'SE': result.SeIterative,'P': result.PvalIterative,'P heterogeneity': result.HetPIterative,'N': len(result.rsname)}
result_df = pd.DataFrame.from_dict(results, orient='index')
result_df['Gene'] = result_df.index.tolist()
result_df
# Alpha Original SE Original P Value Original N Original P heterogeneity Original Alpha SE P P heterogeneity N Gene
#ENSG00000000003 -0.024712 0.068517 0.718346 101.0 1.000000 -0.024712 0.068517 0.718346 1.000000 101 ENSG00000000003
#ENSG00000000419 -0.042308 0.035751 0.236646 123.0 0.957932 -0.042308 0.035751 0.236646 0.957932 123 ENSG00000000419
#ENSG00000000457 0.007607 0.035183 0.828817 123.0 0.942955 0.007607 0.035183 0.828817 0.942955 123 ENSG00000000457

结果表格的表头解释与TWMR大差不差，名称也基本一致。

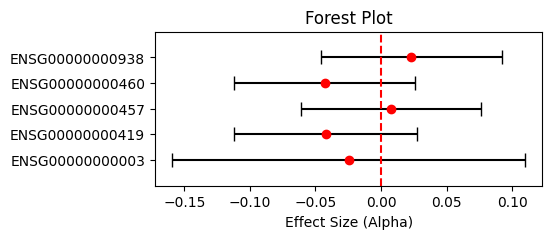
③ 森林图可视化RevTWMR结果:

# 计算置信区间
result_df['CI_lower'] = result_df['Alpha'] - 1.96 * result_df['Standard error']
result_df['CI_upper'] = result_df['Alpha'] + 1.96 * result_df['Standard error']# 森林图可视化
fig, ax = plt.subplots(figsize=(5, 2))
y_positions = [yi+1 for yi in range(len(result_df))]
plt.errorbar(result_df['Alpha'], y_positions,xerr=[result_df['Alpha'] - result_df['CI_lower'], result_df['CI_upper'] - result_df['Alpha']],fmt='o', color='red', ecolor='black', capsize=5)
plt.yticks(y_positions, result_df['Gene'])
plt.ylim(0, max(range(len(result_df['Gene'])))+2)
plt.axvline(x=0, linestyle='--', color='red')plt.xlabel('Causal effect (Alpha)')
plt.title('Forest Plot')
plt.show()