普通仙人掌

参考文献

奆佬YYB的博客 Orz：https://www.cnblogs.com/cjyyb/p/9098400.html

例题

题目

讲解

构造圆方树

这道题目其实就是在仙人掌上面求最近点对。

先说仙人掌的定义吧，每条边都最多在一个简单环上的图就是仙人掌。（简单环就是一个点双联通分量上点和边的数量是一样的）

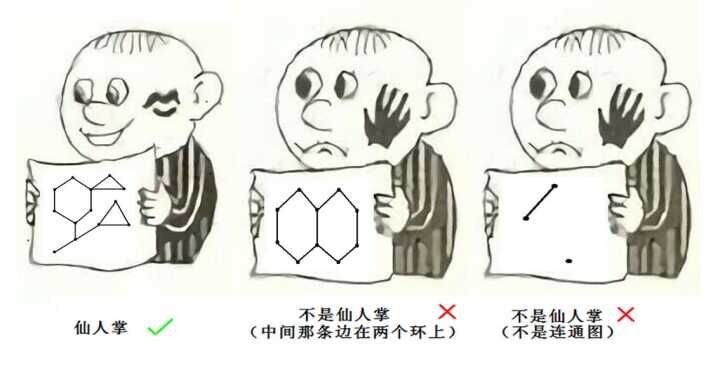
好了，那么我们对于一个简单环，建立一个方点（原图上的点叫圆点），将环上的圆点全部连到方点上面，且对于原图中所有存在于点双联通的边全部删去，没有存在于连通分量的边保留，就成了这样：

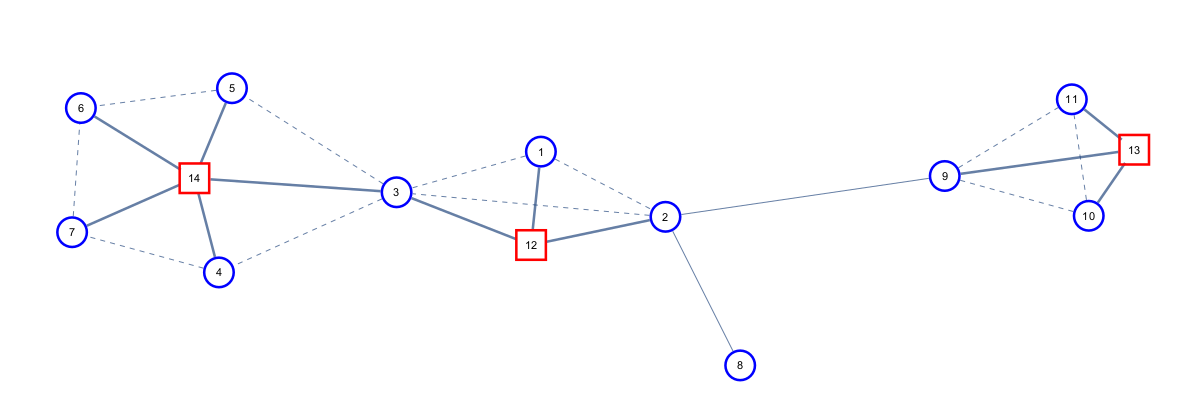
那么如何证明他一定是个树呢。

两步证明，第一步证明其联通，第二步证明其 $∣ V ∣ - 1 = ∣ E ∣$ （边的数量是点的数量减一）。

摘自参考文献（注： $S_T$ 为方点， $R_T$ 为圆点）：

不在环上的边在圆方树中依然存在,

因此这些边连通性不变;

每个环通过新建方点的方式连成一朵菊花,连通性不变。

因此圆方树是无向连通图。

原图中环的个数为 $∣ E ∣ - ∣ V ∣ + 1$ ,则
$V_T|=|S_T|+|R_T|=|V|+|E|−|V|+1=|E|+1,|E_T|=|E|$

(大小为r 的环在仙人掌和圆方树中都是 r 条边),因此满足 $V_T|=|E_T|+1$

圆方树的性质

随便找个圆点为根，方点的父亲是圆点。
随便取一圆点为根，两个点在不断跳父亲的过程中，在相遇之前会跳动同一个环上且跳到的点都不是环上深度最小的点，那么他们的LCA为方点，反之，他们的LCA为圆点。
环中除深度最小的点以外其他点的父亲都是方点。

这道题目的解法

对于这道题目，建立完之后，我们该怎么做呢？

首先确定一个圆点为根，那么整个环中深度最浅的点我们称其为祖先节点 $x$ ，那么环上其他点与方点的边权就是到 $x$ 的最短距离，而方点到 $x$ 的边权为 $0$ ，然后跑LCA。

（以下认为即使他们跳到了一个环上，如果跳到的点是祖先节点，则不认为是跳到同一个环）根据第二个性质，如果LCA为圆点，那么他们不会经过同一个环，而经过不同的环时走方点的边权刚好就等价于在环上跑到环的父亲节点的最小距离，所以用一般树求距离的方法就行了，而对于LCA是方点来说，最多只会有一个相同的环（反正跑到了一个相同的环，在跳一次父亲就是同一个方点了），只要单独对环上这两个点求最短距离即可（至于求法吗，可以处理环上边权总和，然后让他们预处理朝同一个方向跑到祖先节点所经过的边的权值和，这样就可以在询问环上两个点的最小距离的时候 $O (1)$ 求了，当然，细节自己想），

代码

时间复杂度： $O((n+m)\log{n})$

#include<cstdio>
#include<cstring>
#define  N  11000
#define  NN  21000
#define  M  25000
using  namespace  std;
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
inline  int  zabs(int  x){return  x<0?-x:x;}
class  EDGE
{public:struct  node{int  y,next,c;}a[M];int  len,last[N];inline  void  ins(int  x,int  y,int  c){len++;a[len].y=y;a[len].c=c;a[len].next=last[x];last[x]=len;}
}a1,a2;
int  list[N],block,mdis[N]/*表示在环中全部超一个方向的dis*/,sum[N];//所有块的编号 
int  dfn[N],low[N],n,ti,di[N];
int  sta[N],top;
void  build(int  x,int  c)
{int  r=0;for(int  i=top;sta[i]!=x;i--)list[++r]=sta[i];list[++r]=x;//找到环上所有的点 block++;sum[block]=c+di[list[1]]-di[x];//建立分量编号以及边权总和 for(int  i=1;i<r;i++){int  y=list[i];mdis[y]=di[y]-di[x];a2.ins(block+n,y,mymin(sum[block]-mdis[y],mdis[y]));//构建圆方树 }a2.ins(x,block+n,0);
}
void  dfs1(int  x,int  fa)//强连通 
{sta[++top]=x;dfn[x]=low[x]=++ti;for(int  k=a1.last[x];k;k=a1.a[k].next){int  y=a1.a[k].y;if(y!=fa){if(!dfn[y])di[y]=di[x]+a1.a[k].c,dfs1(y,x),low[x]=mymin(low[x],low[y]);else  if(dfn[y]<dfn[x]/*与祖先形成分量*/)low[x]=dfn[y],build(y,a1.a[k].c);}}if(low[x]==dfn[x])a2.ins(fa,x,di[x]-di[fa]);//其是割点且不与其父亲在一个分量上，保留此边 top--;
}int  fa[NN][18],dis[NN]/*到根节点的距离*/,dep[NN]/*层数*/;
void  dfs2(int  x)//求LCA 
{for(int  i=1;i<=15;i++){fa[x][i]=fa[fa[x][i-1]][i-1];if(!fa[x][i])break;}for(int  k=a2.last[x];k;k=a2.a[k].next){int  y=a2.a[k].y;dis[y]=dis[x]+a2.a[k].c;fa[y][0]=x;dep[y]=dep[x]+1;dfs2(y);}
}
inline  int  diss(int  x,int  y)//求两个点的距离 
{if(dep[x]>dep[y])x^=y^=x^=y;int  ans=0,tx=x,ty=y;for(int  i=15;i>=0;i--){if(dep[fa[y][i]]>=dep[x])y=fa[y][i];}if(x==y)return  dis[ty]-dis[y];//直接相遇 for(int  i=15;i>=0;i--){if(fa[y][i]!=fa[x][i])x=fa[x][i],y=fa[y][i];}if(fa[x][0]>n)//方点的情况 {int  shit=zabs(mdis[x]-mdis[y]);return  dis[tx]+dis[ty]-dis[x]-dis[y]+mymin(shit,sum[fa[x][0]-n]-shit);}else  return  dis[tx]+dis[ty]-2*dis[fa[x][0]];
}
int  m,q;
int  main()
{dep[0]=-1;scanf("%d%d%d",&n,&m,&q);for(int  i=1;i<=m;i++){int  x,y,c;scanf("%d%d%d",&x,&y,&c);a1.ins(x,y,c);a1.ins(y,x,c);}dfs1(1,0);dfs2(1);for(int  i=1;i<=q;i++){int  x,y;scanf("%d%d",&x,&y);printf("%d\n",diss(x,y));}return  0;
}

广义仙人掌

参考文献

https://www.cnblogs.com/cjyyb/p/9098400.html

例题

[BeiJing2013]压力
时间限制：10s      空间限制：128MB题目描述
如今,路由器和交换机构建起了互联网的骨架。处在互联网的骨干位置的
核心路由器典型的要处理100Gbit/s的网络流量。他们每天都生活在巨大的压力
之下。
小强建立了一个模型。这世界上有N个网络设备,他们之间有M个双向的
链接。这个世界是连通的。在一段时间里,有Q个数据包要从一个网络设备发
送到另一个网络设备。
一个网络设备承受的压力有多大呢?很显然,这取决于Q个数据包各自走
的路径。不过,某些数据包无论走什么路径都不可避免的要通过某些网络设
备。
你要计算:对每个网络设备,必须通过(包括起点、终点)他的数据包有
多少个?
输入格式
第一行包含3个由空格隔开的正整数N,M,Q。
接下来M行,每行两个整数u,v,表示第u个网络设备(从1开始编号)和
第v个网络设备之间有一个链接。u不会等于v。两个网络设备之间可能有多个
链接。
接下来Q行,每行两个整数p,q,表示第p个网络设备向第q个网络设备发
送了一个数据包。p不会等于q。
输出格式
输出N行,每行1个整数,表示必须通过某个网络设备的数据包的数量。
样例输入
4 4 2
1 2
1 3
2 3
1 4
4 2
4 3
样例输出
2
1
1
2
提示
【样例解释】
设备1、2、3之间两两有链接,4只和1有链接。4想向2和3各发送一个数据
包。显然,这两个数据包必须要经过它的起点、终点和1。
【数据规模和约定】
对于40%的数据,N,M,Q≤2000
对于60%的数据,N,M,Q≤40000
对于100%的数据,N≤100000,M,Q≤200000题目来源：BZOJ

什么，你说BZOJ炸了？

数据？

~~自己找~~

做法

SO，广义圆方树是什么？

其实就是对于一个点双新建一个点，点双中的所有点向他连边。

蒯张图：

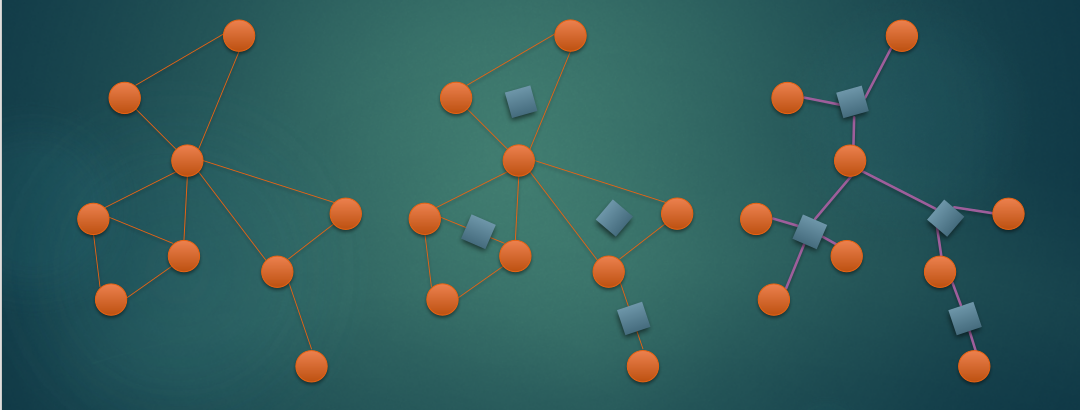
但是这样会导致丢失边的信息，因此只能处理点双的信息，这个东西其实就是类似缩点的一个算法，但是对割点的需求会比较大。

不难发现，一个点双的必经点只有割点、起/终点，直接在圆方树上树上差分即可。

当然，惯例，证明他是一棵树。显然

连通性，点双都连在一个点上，连通性不变。
证明是一棵树，不是树就是环喽。
不难发现，这棵树上严格圆点连方点（只有两个点也是一个点双），方点连圆点，因此存在环的话，一定是方点-圆点-方点-圆点…-方点，的这个一个环。
又不难知道，只有割点才会连接两个及以上的方点，这些圆点就是割点，但是这种情况说明这些割点间存在一个简单环，所以这种情况不成立。（其实就是用了下面的性质2）

代码

#include<cstdio>
#include<cstring>
#define  N  110000
#define  NN  210000
#define  M  410000
using  namespace  std;
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
inline  int  mymax(int  x,int  y){return  x>y?x:y;}
class  EDGE
{public:struct  node{int  y,next;}a[M];int  len,last[NN];void  ins(int  x,int  y){len++;a[len].y=y;a[len].next=last[x];last[x]=len;}
}a1,a2;
int  dfn[N],low[N],ti,n,m,q;
int  sta[N],top,cnt;
void  dfs(int  x)
{dfn[x]=low[x]=++ti;sta[++top]=x;for(int  k=a1.last[x];k;k=a1.a[k].next){int  y=a1.a[k].y;if(!dfn[y]){dfs(y);low[x]=mymin(low[x],low[y]);if(low[y]==dfn[x]){cnt++;while(sta[top]!=y)a2.ins(cnt+n,sta[top--]);top--;a2.ins(cnt+n,y);a2.ins(x,cnt+n);}}else  low[x]=mymin(dfn[y],low[x]);}
}
int  tot[NN];
void  dfs2(int  x)
{for(int  k=a2.last[x];k;k=a2.a[k].next){int  y=a2.a[k].y;dfs2(y);tot[x]+=tot[y];}
}
int  fa[NN][20],dep[NN];//17
void  dfs3(int  x)
{for(int  i=1;i<=17;i++){fa[x][i]=fa[fa[x][i-1]][i-1];if(!fa[x][i])break;}for(int  k=a2.last[x];k;k=a2.a[k].next){int  y=a2.a[k].y;fa[y][0]=x;dep[y]=dep[x]+1;dfs3(y);}
}
inline  int  lca(int  x,int  y)
{if(dep[x]>dep[y])x^=y^=x^=y;for(int  i=17;i>=0;i--){if(dep[fa[y][i]]>=dep[x])y=fa[y][i];}if(x==y)return  x;for(int  i=17;i>=0;i--){if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];}return  fa[x][0];
}
int  main()
{
//	freopen("1.in","r",stdin);
//	freopen("1.out","w",stdout); dep[0]=-1;scanf("%d%d%d",&n,&m,&q);for(int  i=1;i<=m;i++){int  x,y;scanf("%d%d",&x,&y);a1.ins(x,y);a1.ins(y,x);}dfs(1);dfs3(1);for(int  i=1;i<=q;i++){int  x,y;scanf("%d%d",&x,&y);int  z=lca(x,y);tot[x]++;tot[y]++;tot[z]--;tot[fa[z][0]]--;}dfs2(1);for(int  i=1;i<=n;i++)printf("%d\n",tot[i]);return  0;
}