目录

引言

栈的定义

栈的分类

栈的功能

栈的声明

1.顺序栈

2.链式栈

栈的功能实现

1.栈的初始化

(1)顺序栈

(2)链式栈

(3)复杂度分析

2.判断栈是否为空

(1)顺序栈

(2)链式栈

(3)复杂度分析

3.返回栈顶元素

(1)顺序栈

(2)链式栈

(3)复杂度分析

4.返回栈的大小

(1)顺序栈

(2)链式栈

(3)复杂度分析

5.元素入栈

(1)顺序栈

(2)链式栈

(3)复杂度分析

6.元素出栈

(1)顺序栈

(2)链式栈

(3)复杂度分析

7.打印栈的元素

(1)顺序栈

(2)链式栈

(3)复杂度分析

8.销毁栈

(1)顺序栈

(2)链式栈

(3)复杂度分析

顺序栈和链式栈的对比

完整代码

1.顺序表

2.链式表

结束语

---

引言

在学习完链表之后，我们接下来学习数据结构——栈的内容。

栈的定义

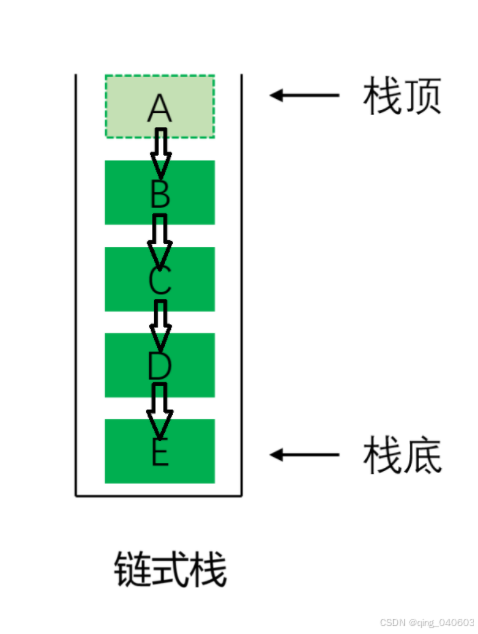
栈（Stack）是一种遵循后进先出（LIFO, Last In First Out）原则的有序集合。这种数据结构只允许在栈顶进行添加（push）或删除（pop）元素的操作。换句话说，最后添加到栈中的元素将是第一个被移除的，就像一叠盘子那样，我们只能从上面开始取放盘子。

如图所示：

栈顶（Top）：栈顶是栈中最后添加（push）元素的位置，也是最先被移除（pop）或查看（peek/top）的元素所在的位置。在栈的所有操作中，无论是添加、删除还是查看元素，都是针对栈顶进行的。因此，栈顶是栈中最活跃、最频繁被访问的位置。

栈底（Bottom）：栈底是栈中最早被添加进去的元素所在的位置，也是栈中唯一一个固定不变的位置（除非整个栈被清空）。在栈的常规操作中，栈底元素不会被直接访问，除非是将整个栈的内容倒序输出或者栈被完全清空。因此，栈底在栈的操作中扮演的是一个相对静态的角色。

栈的分类

栈可以分为顺序栈与链式栈。

如下图所示：

顺序栈：

链式栈：

栈的功能

我们要实现的栈的功能如下所示：

1.栈的初始化。
2.判断栈是否为空。
3.返回队头元素。
4.返回栈的大小。
5.元素入栈。

6.元素出栈。
7.打印栈的元素。
8.销毁栈。

栈的声明

1.顺序栈

顺序栈的声明需要一个指向一块空间的指针a，指向栈顶下一个元素的top，以及标志栈空间大小的capacity。

声明如下：

typedef int STDataType;typedef struct STDataType
{STDataType* a;int top;int capacity;
}ST;

2.链式栈

链式栈的声明只需要一个top指针，以及栈的容量capacity。

当然这里需要链表的声明。

代码如下：

typedef int STDataType;typedef struct SListNode
{STDataType data;struct SListNode* next;
}SLTNode;typedef struct Stack
{// 指向栈顶节点的指针SLTNode* top;int size;
}ST;

栈的功能实现

1.栈的初始化

顺序栈和链式栈都可以先初始为NULL。

(1)顺序栈

顺序栈可以将top设置为-1，capacity设置为0。

代码如下：

//栈的初始化
void STInit(ST* st)
{assert(st);st->a = NULL;st->top = -1;st->capacity = 0;
}

(2)链式栈

链式栈将size设置为0，top设置为NULL。

代码如下：

//栈的初始化
void STInit(ST* st)
{assert(st);st->size = 0;st->top = NULL;
}

(3)复杂度分析

时间复杂度：由于顺序栈和链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

2.判断栈是否为空

判断栈是否为空只需要判断top的指向。

(1)顺序栈

当top=-1则为空。

代码如下：

//判空
bool STEmpty(ST* st)
{assert(st);return st->top == -1;
}

(2)链式栈

判断top是否指向NULL。

代码如下：

//判空
bool STEmpty(ST* st)
{return (st->top == NULL);
}

(3)复杂度分析

时间复杂度：由于顺序栈和链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

3.返回栈顶元素

(1)顺序栈

//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);// 断言确保栈不为空（即栈顶索引不小于0）assert(st->top >= 0);return st->a[st->top];
}

(2)链式栈

//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(!STEmpty(st));return st->top->data;
}

(3)复杂度分析

时间复杂度：由于顺序栈和链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

4.返回栈的大小

(1)顺序栈

由于在一开始将top设置为-1，需要top+1才能符合需要。

代码如下：

//获取数据个数
STDataType STSize(ST* st)
{assert(st);return st->top + 1;
}

(2)链式栈

//获取数据个数
STDataType STSize(ST* st)
{return st->size;
}

(3)复杂度分析

时间复杂度：由于顺序栈和链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

5.元素入栈

注意：入栈需要检查空间是否足够。

(1)顺序栈

由于top设置的是-1，因此需要先腾出空间然后再将新元素x放在栈顶。

代码如下：

//入栈
void STPush(ST* st, STDataType x)
{assert(st);// 注意：由于top初始化为-1，所以满的条件是top == capacity - 1if (st->top == st->capacity - 1){// 如果栈已满，则扩展栈的容量int newcapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail：");return;}st->a = tmp;st->capacity = newcapacity;}// 增加栈顶索引，为新元素腾出空间st->top++;// 将新元素x存储在栈顶位置st->a[st->top] = x;
}

(2)链式栈

//入栈
void STPush(ST* st, STDataType x)
{SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));if (newnode == NULL){perror("malloc fail:");return;}// 新节点的next指向原来的栈顶newnode->next = st->top;// 设置新节点的数据newnode->data = x;// 更新栈顶为新节点st->top = newnode;st->size++;
}

(3)复杂度分析

时间复杂度：由于顺序栈支持下标的随机访问并且我们以单链表的头作为栈顶，因此时间复杂度为O(1)。

空间复杂度：顺序表又可能需要进行扩容处理，最坏的情况是空间复杂度为O(n)。链式表每次入栈固定为一个节点，因此空间复杂度为O(1)。

6.元素出栈

(1)顺序栈

//出栈
void STPop(ST* st)
{assert(st);assert(st->top >= 0);st->top--;
}

(2)链式栈

//出栈
void STPop(ST* st)
{assert(st);assert(!STEmpty(st));// 获取栈顶节点的下一个节点SLTNode* next = st->top->next;free(st->top);// 更新栈顶指针，使其指向新的栈顶节点st->top = next;st->size--;
}

(3)复杂度分析

时间复杂度：由于顺序栈还是链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

7.打印栈的元素

(1)顺序栈

//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));// 从栈顶开始打印，直到栈底（但不包括索引-1）for (int i = st->top; i >= 0; i--){printf("%d ", st->a[i]);}
}

(2)链式栈

//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));for (SLTNode* top = st->top; top != NULL; top = top->next){printf("%d ", top->data);}
}

(3)复杂度分析

时间复杂度：由于顺序栈和链式栈打印都需要遍历整个栈，因此时间复杂度为O(N)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

8.销毁栈

(1)顺序栈

//栈的销毁
void STDestory(ST* st)
{assert(st);free(st->a);st->a = NULL;st->capacity = 0;st->top = -1;
}

(2)链式栈

//栈的销毁
void STDestory(ST* st) 
{assert(st);SLTNode* top = st->top;while (top != NULL){SLTNode* next = top->next;free(top);top = next;}st->size = 0;
}

(3)复杂度分析

时间复杂度：由于顺序栈还是链式栈花费时间都是一个常数，因此时间复杂度为O(1)。

空间复杂度：由于顺序栈和链式栈花费空间都是一个固定大小的空间，因此空间复杂度为O(1)。

顺序栈和链式栈的对比

	顺序栈	链式栈
数据结构	使用动态数组实现，元素在物理内存中连续存储	使用链表实现，元素通过节点和指针连接，内存空间不连续
内存管理	栈空间不足时可动态扩容，释放整个栈时一次性释放内存	节点内存单独分配和释放，需要遍历链表以释放所有节点内存
时间效率	可以通过数组下标直接访问栈内任意位置的元素，但是这不符合栈的定义	由于每次都需要扩容操作，所以效率略比顺序栈低
空间效率	顺序栈的扩容较大可能会造成空间的浪费	内存使用相对灵活，但每个节点需要额外存储指针

完整代码

1.顺序表

Stack.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;typedef struct STDataType
{STDataType* a;int top;int capacity;
}ST;//栈的初始化
void STInit(ST* st);//栈的销毁
void STDestory(ST* st);//入栈
void STPush(ST* st, STDataType x);
//出栈
void STPop(ST* st);//取出栈顶数据
STDataType STTop(ST* st);//判空
bool STEmpty(ST* st);//获取数据个数
STDataType STSize(ST* st);//栈的打印
void STPrint(ST* st);

Stack.c

#include"Stack.h"//栈的初始化
void STInit(ST* st)
{assert(st);st->a = NULL;st->top = -1;st->capacity = 0;
}//栈的销毁
void STDestory(ST* st)
{assert(st);free(st->a);st->a = NULL;st->capacity = 0;st->top = -1;
}//入栈
void STPush(ST* st, STDataType x)
{assert(st);// 注意：由于top初始化为-1，所以满的条件是top == capacity - 1if (st->top == st->capacity - 1){// 如果栈已满，则扩展栈的容量int newcapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail");return;}st->a = tmp;st->capacity = newcapacity;}// 增加栈顶索引，为新元素腾出空间st->top++;// 将新元素x存储在栈顶位置st->a[st->top] = x;
}//出栈
void STPop(ST* st)
{assert(st);assert(st->top >= 0);st->top--;
}//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(st->top >= 0);return st->a[st->top];
}//判空
bool STEmpty(ST* st)
{assert(st);return st->top == -1;
}//获取数据个数
STDataType STSize(ST* st)
{assert(st);return st->top + 1;
}//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));// 从栈顶开始打印，直到栈底（但不包括索引-1）for (int i = st->top; i >= 0; i--){printf("%d ", st->a[i]);}
}

2.链式表

Stack.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;typedef struct SListNode
{STDataType data;struct SListNode* next;
}SLTNode;typedef struct Stack
{// 指向栈顶节点的指针SLTNode* top;int size;
}ST;//栈的初始化
void STInit(ST* st);//栈的销毁
void STDestory(ST* st);//入栈
void STPush(ST* st, STDataType x);//出栈
void STPop(ST* st);//取出栈顶数据
STDataType STTop(ST* st);//判空
bool STEmpty(ST* st);//获取数据个数
STDataType STSize(ST* st);//栈的打印
void STPrint(ST* st);

Stack.c

#include"Stack.h"//栈的初始化
void STInit(ST* st)
{assert(st);st->size = 0;st->top = NULL;
}//栈的销毁
void STDestory(ST* st) 
{assert(st);SLTNode* top = st->top;while (top != NULL){SLTNode* next = top->next;free(top);top = next;}st->size = 0;
}//入栈
void STPush(ST* st, STDataType x)
{SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));if (newnode == NULL){perror("malloc fail:");return;}// 新节点的next指向原来的栈顶newnode->next = st->top;// 设置新节点的数据newnode->data = x;// 更新栈顶为新节点st->top = newnode;st->size++;
}//出栈
void STPop(ST* st)
{assert(st);assert(!STEmpty(st));// 获取栈顶节点的下一个节点SLTNode* next = st->top->next;free(st->top);// 更新栈顶指针，使其指向新的栈顶节点st->top = next;st->size--;
}//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(!STEmpty(st));return st->top->data;
}//判空
bool STEmpty(ST* st)
{return (st->top == NULL);
}//获取数据个数
STDataType STSize(ST* st)
{return st->size;
}//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));for (SLTNode* top = st->top; top != NULL; top = top->next){printf("%d ", top->data);}
}

结束语

本篇博客简要介绍了一下栈，接下来我们将接着学习与栈有些类似的另一个数据结构——队列。

数据结构——链式队列和循环队列

感谢各位大佬们的支持！！！

求点赞收藏关注！！！

十分感谢！！！