二分图总结
- 前言
- 二分图总结
- 二分图基本概念
- 什么是二分图?
- 二分图图的性质
- 染色法判断是否有奇环
- 二分图匹配算法
- 匹配概念
- 匈牙利算法
- 二分图最小点覆盖
- 2,3号边
- 1,4号边
- 小结
- 二分图最小边覆盖
- 二分图最小路径覆盖
- 二分图最大独立集
前言
这篇文章是作者在学完二分图的总结,由于作者比较弱,可能只总结了一些皮毛,如果有错误,请大佬指正
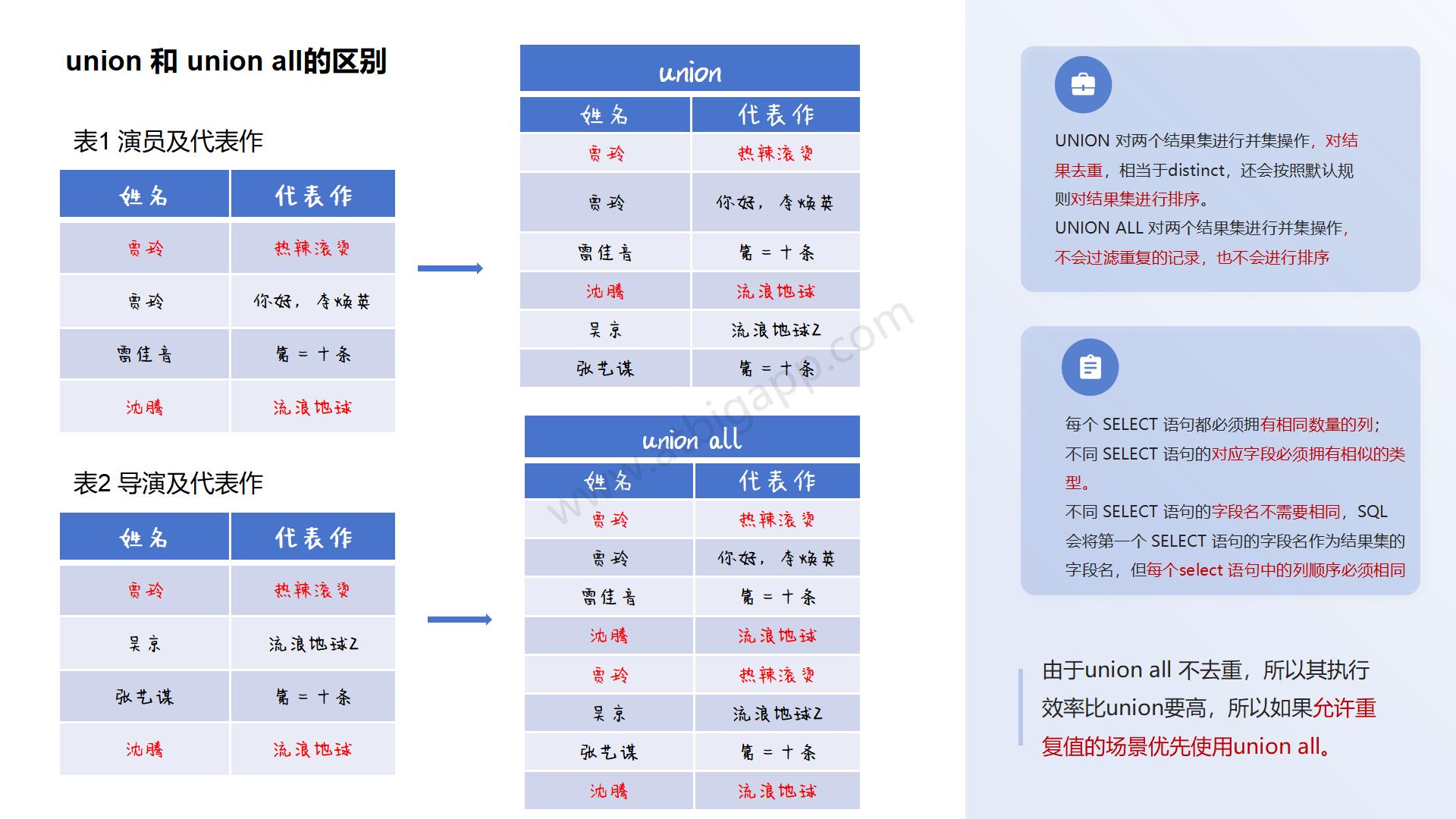
二分图总结
二分图基本概念
什么是二分图?
二分图就像名字说的那样,将一幅图二分了,分成两个点集(U,V),并且每一条边都连接着UV**(重!!!:二分图任意点集的点不能连向此点集的点,如U点集的**
点不能连接U点集的点)。
二分图图的性质
二分图有一个性质:二分图没有奇环。
在一幅图中不能含有奇环,有就说明此图不是二分图。
为什么呢?若含有奇环,那么以相邻两条边表示这两个点属于不同的点集,但是若跑完整个奇
环后,就会出现两个属于相同的点集的两个点,这样的话不就不符合相同点集的点不能相连
了嘛。
染色法判断是否有奇环
染色法其实就是将一个图,分成UVUVUV…这样子,相当于将图分成两个不同的点集,也就是
相邻点不属于同一点集,并进行编号,若冲突表示相邻点的点集相同了则不是二分图。
举个例子:

1和2相邻,故不同,标称U,V。2和3 相邻,不同,但2已经是V,所以3是U。1和3相邻,故不同,但实际上1和3是相同的,矛盾,不是二分图。
那么代码可以怎么写呢?
我们采用奇偶染色(染色法),就是121212…变换就可以直接用3去减相邻的,比如3-1=2,3-2=1,相当于直接改变了,且改变了奇偶性,所以叫奇偶染色。
bool dfs(int u, int f)
{for (int i = head[u]; i != -1; i = nxt[i]){int v = to[i];if (v != f){if (!belong[v]){belong[v] = 3 - belong[u];if (!dfs(v, u)) return false;}else if (belong[v] == belong[u]) return false;}}return true;
}
二分图样貌展示:

二分图匹配算法
匹配概念
匹配是指一些边的集合,称作匹配,而这些边指的是二分图两边的点集相连的边(注意:匹配的任意两个边的没有公共点!!!)。
一个匹配中的边的集合中的边,都叫匹配边,如果不在次集合内的边叫非匹配边;而匹配边的两头的点的集合叫做匹配点,也叫盖点,没有在此点集内的,叫未盖点(非匹配点)。
若有一种匹配,它是所有匹配中边的数量最多的,那么我们称其为最大匹配。
二分图中还有一个种匹配,叫完美匹配:二分图中的某个匹配,使得所有点都成了盖点,那么此时就是完美匹配。

匈牙利算法
匈牙利算法本质是一个找增广路的一个算法,因为若出现一条增广路,当前匹配A,肯定会到达匹配B,且B的匹配边的个数是匹配A加1,换句话说,出现增广路,那么我们记录的最大匹配的个数加1。
那什么是增广路呢?
首先增广路肯定是条路径对吧,增广路就是指从左边任意一点到右边任
意一点的路径(注:增广路的以右边未盖点结尾),如这样(U为左点集,V为右点集):U-V-U-V…-U-V的交错路径。
为什么找到增广路最大匹配的个数就加1呢?
一旦出现增广路,路径上的点就会更新新的左或
右的点(换句话说就是更换一下另一半的匹配点),而当更换完成另一半后,自然会空出一个位置,而又因为它是一条路径,自然是相通的,所以那个位置就可以给上面的一个点去匹配,那么因为最后的点是未盖点,所以此时这条路径上的匹配就会增加。举个例子子:如下图是一个增广路,如果没有下面一条边,只能匹配一条边,如果加上了呢?你会发现无论上面的匹配边是哪条,在加上最下面的边之后总会增加匹配(最上面的一条是匹配边得话,左边的第二个点可直接匹配右下角的点,匹配边是第二条的话,也能更换成最下面的匹配边,然后上面又能匹配了)
那么代码该如何写呢?
我们可以采用dfs搜索的写法,每一次枚举左边点集,然后看看右边点集是否构成增广路,不断执行下去。
#define mem(a,b) memset(a,b,sizeof(a))
int vis[N];
int px[N], py[N];
void add(int a, int b)
{to[++E] = b;nxt[E] = head[a];head[a] = E;
}
bool dfs(int x)
{for (int i = head[x]; ~i; i = nxt[i]){int v = to[i];if(!vis[v]){vis[v] = 1;if(py[v] == -1 || dfs(py[v])) //如果到尽头或下面找到尽头了,更新{py[v] = x;px[x] = v;return true;}}return false;
}
void work(int n)
{mem(px, -1);mem(py, -1);for (int i = 1; i <= n; ++i){ mem(vis, 0);if(dfs(i)) ++ret;}
}
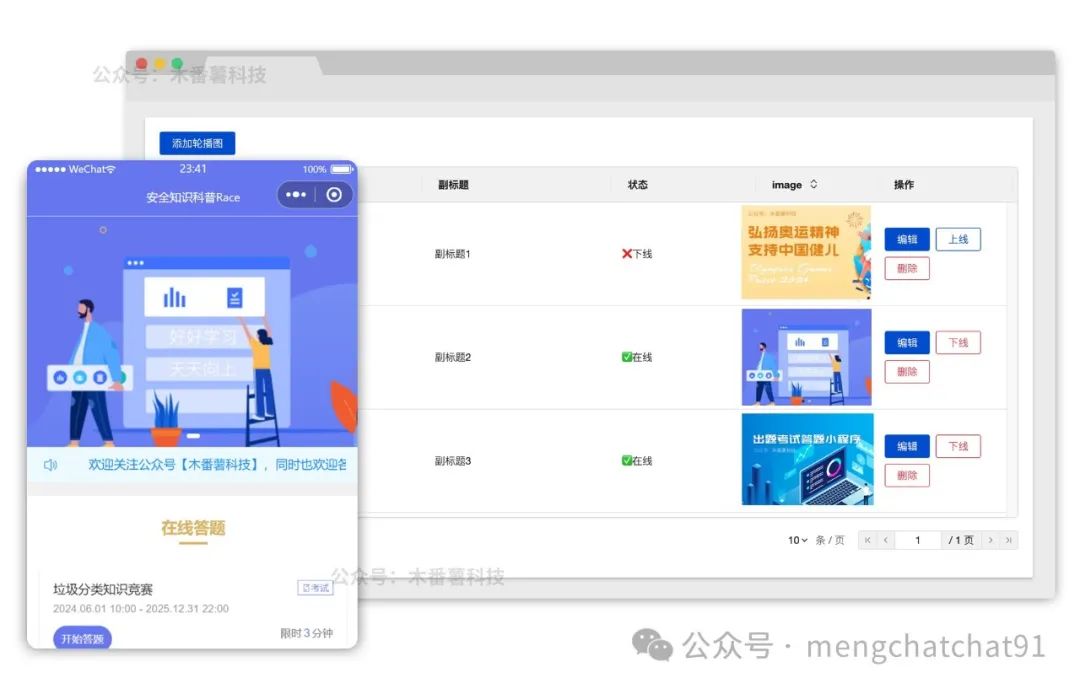
二分图最小点覆盖
二分图最小点覆盖自然是用最少的点去覆盖二分图所有的边。
此问题我们可以先跑一遍最大匹配,再将其分成四个情况:
1:匹配边
2:左盖右未盖
3:左未盖右盖
4:左右都盖
2,3号边
只需要选已盖点就行了。不过若2,3号边的已盖点在同一条边怎么办?
其实根本就不用担心,若存在这种情况,必定会出现增广路,但此时已经是最大匹配,就与前面冲突,矛盾,所以不存在这种情况。
1,4号边
问题主要在上面的2,3号边没选到1,4号边的盖点怎么办?其实若没有的话,证明没有一个未盖点能到达1,4号边的盖点,所以左右随便选。
小结
至此,我们搞定所有情况,如此看来,最小点覆盖就是最大匹配的边数,也就是最小点覆盖等于最大匹配。
二分图最小边覆盖
二分图最小边覆盖自然就是用最少的边数覆盖所有点。
分析一下,除去我们的最大匹配,剩下的n-ans * 2个点就用同样多的边去覆盖(ans为最大匹配)。
为什么呢?
想一下,若存在两个未盖点中间有边,那么最大匹配就不是ans了,又因为ans是最大匹配,矛盾,故不会出现这种情况。
还有,要注意,因为不存在两个未盖点之间有条边,那么两头之间肯定有盖点,可是之前已经覆盖过了,所以要舍弃那一半的盖点和边。
最终,答案就是n - ans * 2 + ans,由于重复了ans条边,故要减去。
二分图最小路径覆盖
一个有向图,用最少且不相交的路径覆盖所有的点。
我们可以将图转化成二分图,左边表示出度,右边表示入度。那么刚开始的路径个数就是n。
我们可以跑一遍最大匹配,在跑的过程中,若匹配加1,证明出现了增广路, 那么此时就说明可以省去一条路径了, 所以最大匹配等于最大能省去多少条路径,那么最小路径覆盖就等于n-最大匹配。
二分图最大独立集
独立集:⼀个点集,点集内的点两两不相邻
若刚开始时选了所有点,那么连边的肯定得删去一头,但是至于删哪边,我们要考虑删连边
的多的,这样的话可以切断许多连通。
但是最小点覆盖正是选连边多的,所以最大独立集就可以是n-最小点覆盖
匹配等于最大能省去多少条路径,那么最小路径覆盖就等于n-最大匹配。