【hot100篇-python刷题记录】【滑动窗口最大值】

R6-子串篇

Max

Sort

单调队列法：

Max

完了，我好像想到python的max

class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:ret=[]left,right=0,kwhile right<=len(nums):ret.append(max(nums[left:right]))right+=1left+=1return ret

居然超时

分析一下时间复杂度

外层循环的次数：外层循环会遍历整个数组 nums，每次增加 left 指针。循环的次数是 len(nums) - k + 1，因为当 left 到达 len(nums) - k 时，窗口的右边界 right 将是 len(nums)，这是窗口能滑动的最后一个位置。
内层 max 函数的调用：在每次外层循环中，max 函数会被调用，以找到当前窗口中的最大值。由于窗口的大小是固定的 k，因此每次调用 max 函数的时间复杂度是 O(k)。
结合这两个方面，我们可以得到以下的时间复杂度：外层循环的次数是 len(nums) - k + 1，每次循环中，我们调用 max 函数，其时间复杂度是 O(k)。因此，总的时间复杂度是：O((len(nums) - k + 1) * k)这可以简化为：O((n - k + 1) * k)其中 n 是数组 nums 的长度。如果 k 相对于 n 来说是常数，那么时间复杂度可以进一步简化为：O(n * k)这是因为 k 被视为常数，因此可以忽略。综上所述，给定代码的时间复杂度是 O(n * k)。

Sort

还想用sort蒙混过关哈哈哈

class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:ret=[]left,right=0,kwhile right<=len(nums):sort_nums=sorted(nums[left:right])ret.append(sort_nums[-1])right+=1left+=1return ret

一样超时

只能尽可能少的-地在内层循环中搜索值

我也这样想过

这个题解解决了现有的问题

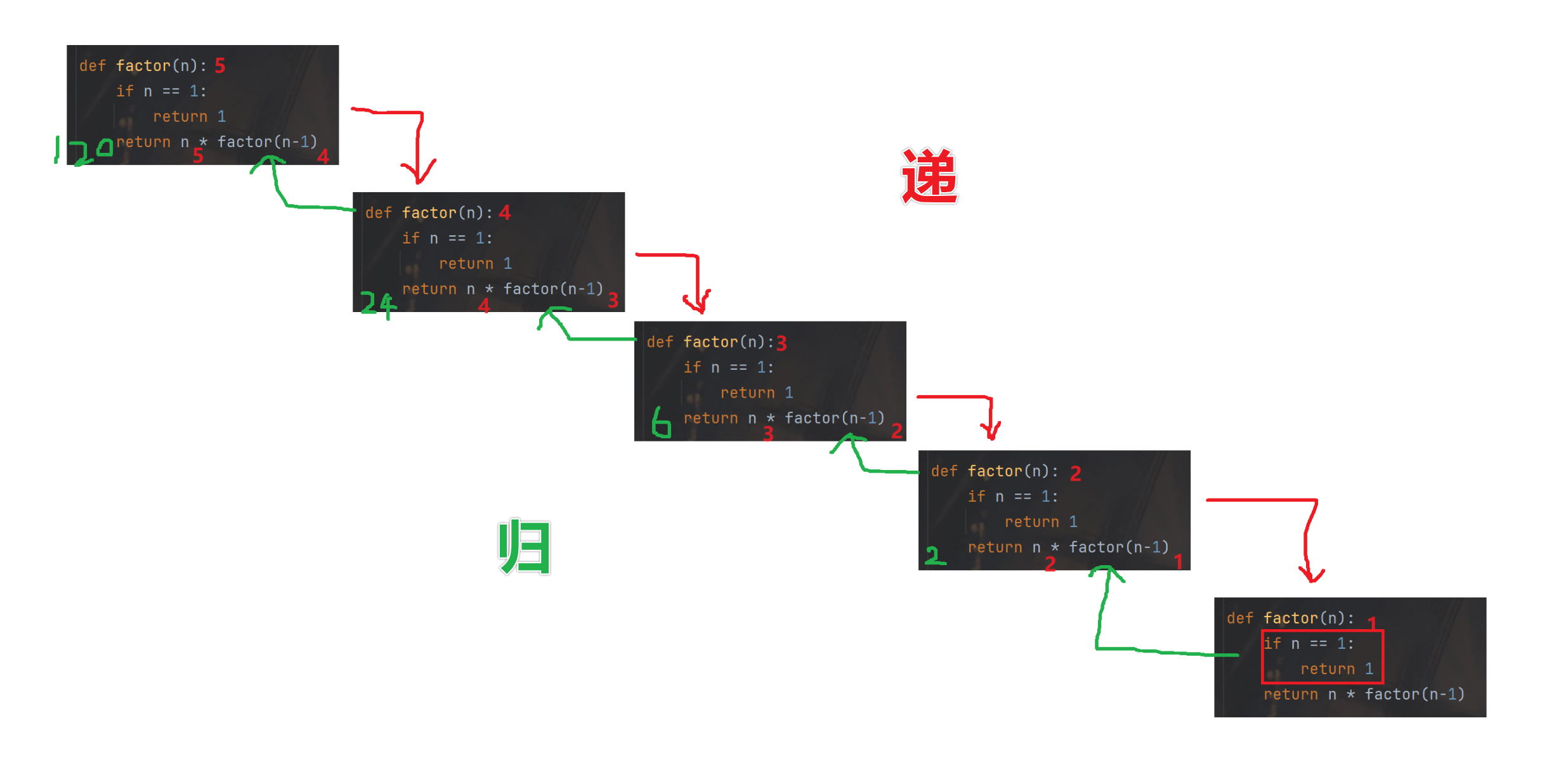
本题难点：怎么将内层的查找最大值，O(k)压缩至O(1)

单调队列法：

直接看代码吧

class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:#创建队列deque=collections.deque()ret,n=[],len(nums)for i,j in zip(range(1-k,n+1-k),range(n)):#删除deque中对应的nums[i-1]if i>0 and deque[0]==nums[i-1]:deque.popleft()#保持deque递减while deque and deque[-1]<nums[j]:deque.pop()deque.append(nums[j])#记录窗口最大值if i>=0:ret.append(deque[0])return ret