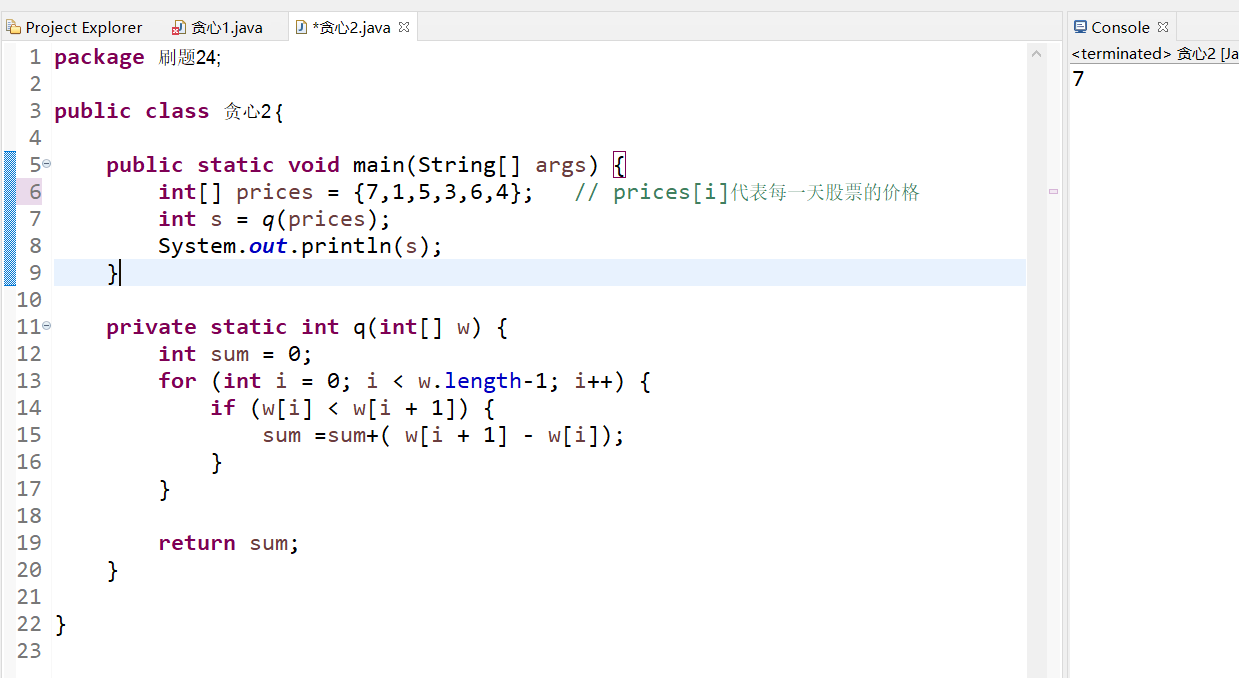
本解法是股票问题的通用解法,在leetcode上对应以下题:
买卖股票的最佳时机
买卖股票的最佳时机 II
买卖股票的最佳时机 III
买卖股票的最佳时机 IV
买卖股票的最佳时机含手续费
最佳买卖股票时机含冷冻期
下面来说通用解法:
这类问题有一个状态转移图:
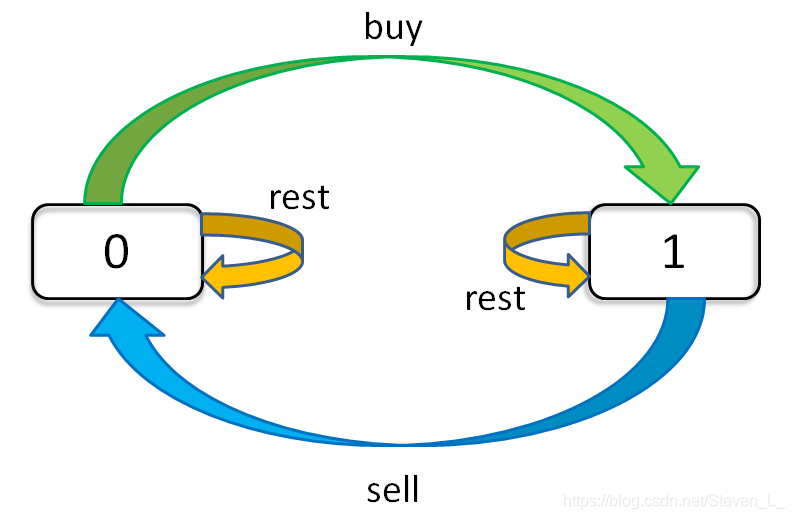
其中:0表示未持有股票,1表示持有股票。则对应于每一天,有持有和未持有两种情况。
如果某一天持有股票,则可能是前一天就已持有股票或前一天未持有股票,当天买入了股票;如果某一天未持有股票,则可能是前一天就未持有股票或前一天持有股票,当天卖出了股票。
那么很容易得到如下递推式:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
// max( 选择 rest , 选择 sell )
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
// max( 选择 rest , 选择 buy )
解释一下:三维dp数组i表示第i天,k表示第k手,0表示当天未持有股票,1表示当天持有股票。
利用以上解法就能轻松解出股票买卖问题了,以下分别说明:
- k=1
对应只能买卖一次的情况
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) = max(dp[i-1][1][1], -prices[i])// 由于k均为1,可以简化为:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])
- k无限制
对应无限次买卖的情况
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])= max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])// 这里k仍然没有意义,简化为:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
- k无限制,有冷却时间
// 这里k仍简化:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
- k无限制,有手续费
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
- k不为1或不限制的情况
这时k不能简化,因此转移方程如下:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
以k为指定值为例(没有任何简化的情况),写出解答代码:
class Solution {public int maxProfit(int k, int[] prices) {int[][][] dp = new int[prices.length+1][k+1][2];for(int i=0;i<=k;i++){dp[0][i][0]=0;dp[0][i][1]=Integer.MIN_VALUE; // 表示不可能}for(int i=1;i<=prices.length;i++){for(int j=1;j<=k;j++){ // 0次交易 值为0 无需处理dp[i][j][0]=Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i-1]);dp[i][j][1]=Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i-1]);}}return dp[prices.length][k][0];}}