目录
题目描述
示例1:
示例2:
提示:
解题思路
Collections库
介绍
滑动窗口法
概念
应用场景及特点:
思路
流程展示
代码
复杂度分析
题目描述
给定两个字符串s和p,找到s中所有p的异位词的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词指由相同字母重排列形成的字符串(包括相同的字符串)。
示例1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例2:
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
- 1 <= s.length, p.length <= 3 * (10**4)
s和p仅包含小写字母
解题思路
Collections库
介绍
Python的collections库是一个内建模块,它提供了一系列特殊的容器数据类型,用于扩展Python的标准内建容器(如字典、列表、集合和元组)。这些特殊的容器类型提供了比通用数据类型更多的选择和更好的性能,非常适合在需要高效数据处理和复杂数据结构时使用。
- 具体使用详情
- 官方地址
滑动窗口法
概念
滑动窗口是一个在序列上移动的区间,通常由左右两个指针来界定这个区间的范围。通过移动指针来改变窗口的大小和位置,在窗口移动的过程中,根据问题的需求进行特定的计算和处理。
应用场景及特点:
- 子数组 / 子串问题:
- 当需要在一个序列中找到满足特定条件的连续子数组或子串时,滑动窗口非常适用。例如,寻找和为特定值的连续子数组、含有特定字符的最长子串等。
- 窗口的大小通常是动态变化的,根据问题的条件进行调整。
- 高效性:
- 相比于暴力枚举所有可能的子数组 / 子串,滑动窗口法通常能够在更短的时间内找到解。因为它利用了子数组 / 子串的连续性和窗口的滑动特性,避免了重复计算。
- 指针移动规则:
- 通常有两个指针,一个指向窗口的左端,一个指向窗口的右端。根据问题的具体要求,以特定的方式移动指针。
- 例如,在寻找满足特定条件的最小子数组时,可能会先扩大窗口直到满足条件,然后再缩小窗口以找到最小的满足条件的窗口。
思路
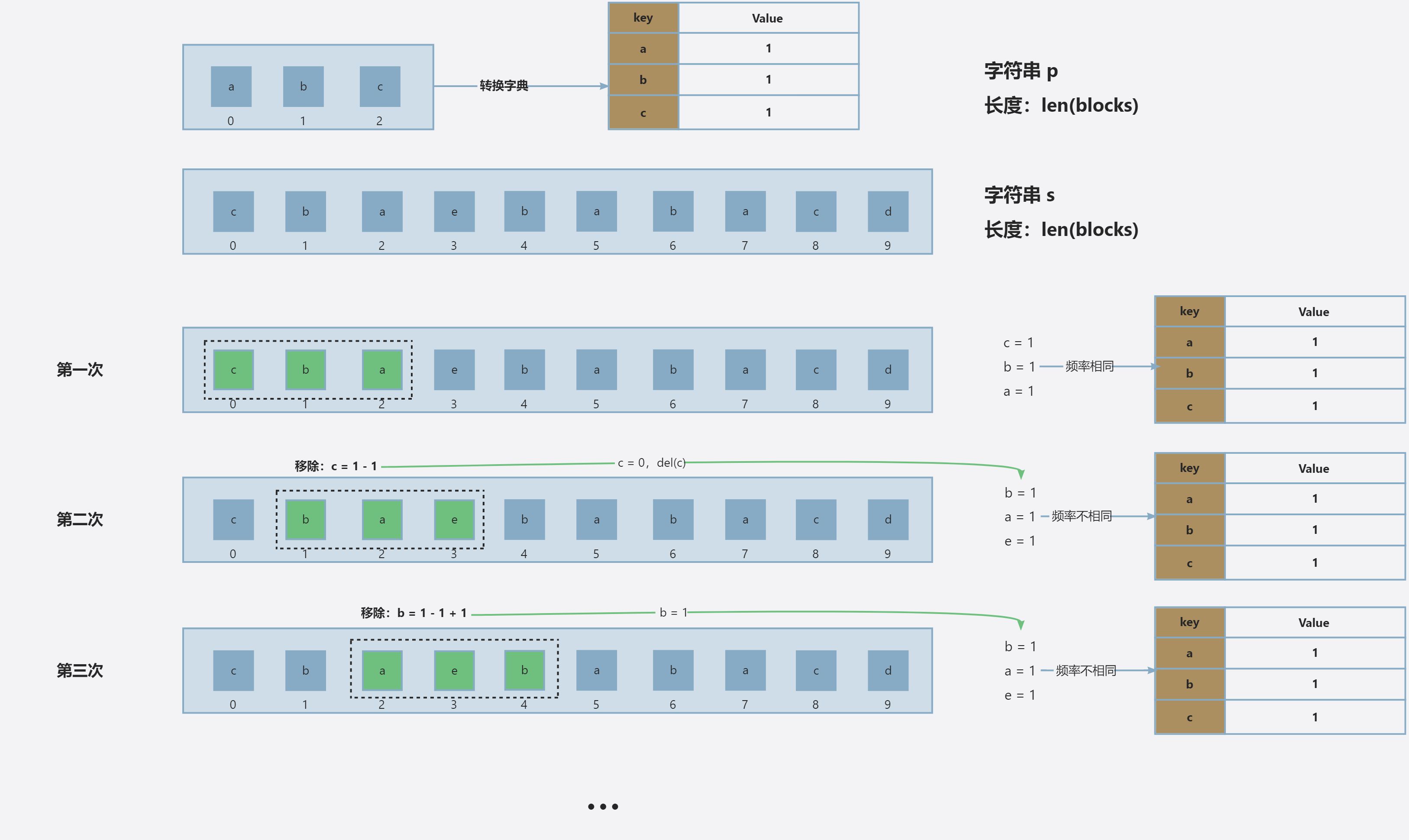
这道题可以使用滑动窗口(Sliding Window)和哈希表的结合来解决。解题的关键是如何有效地在字符串 s 中找到与字符串 p 的异位词相同的子串。
- 异位词特征:两个字符串是异位词,那么它们每个字符的出现次数是相同的。因此,我们可以使用字符频率来判断一个子串是否是异位词。
- 滑动窗口:我们在字符串
s上维护一个大小为len(p)的滑动窗口,记录窗口内的字符频率。当窗口的大小等于p的长度时,我们检查窗口内的字符频率是否和p的字符频率相同。如果相同,则说明当前窗口是p的一个异位词,我们记录下窗口的起始索引。 - 窗口滑动:每次窗口滑动时,我们更新窗口的字符频率,移出窗口左边的一个字符,并添加右边新进入窗口的字符。
流程展示
代码
class Solution: def findAnagrams(self, s: str, p: str) -> List[int]: res = []n, m = len(s), len(p)if n < m:return res# 初始化p的字符频率p_count = collections.Counter(p)# 初始化窗口的字符频率window = collections.Counter(s[:m-1])for i in range(m-1, n):# 增加新的字符到窗口window[s[i]] += 1# 如果窗口字符频率和p字符频率相同,记录起始索引if window == p_count:res.append(i - m + 1)# 移除左边的字符,保持窗口大小为mwindow[s[i - m + 1]] -= 1if window[s[i - m + 1]] == 0:del window[s[i - m + 1]]return res复杂度分析
- 时间复杂度:
O(n),其中n是字符串s的长度。遍历字符串s需要O(n)时间,在每次窗口移动时,我们对窗口内的字符进行更新和比较,哈希表的比较是O(1),因此总时间复杂度是O(n)。 - 空间复杂度:
O(m),其中m是字符串p的长度。我们使用了两个哈希表来存储字符频率,每个哈希表最多存储m个不同的字符,因此空间复杂度是O(m)。