509. 斐波那契数
题目链接:斐波那契数
递归(暴搜)
斐波那契数列,最传统的解法,采用递归:
class Solution {
public:int fib(int n){return dfs(n);}int dfs(int n){if(n == 0 || n == 1)return n;return dfs(n-1) + dfs(n-2);}
};
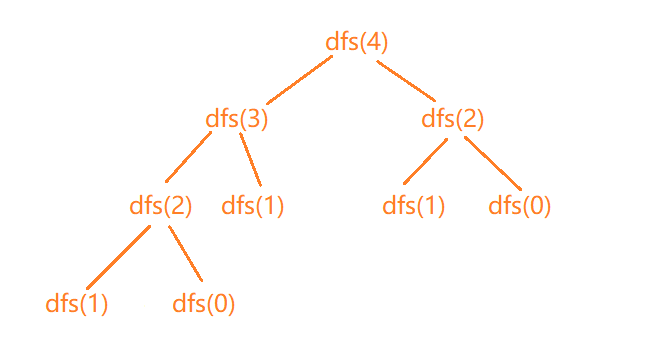
当n = 4的时候,虽然不是满二叉树,但是高度有4层,时间复杂度可以理解为O(2n)。
记忆化搜索
这里递归展开,就会发现,做了很多次重复的递归,在此基础上可以将其优化,将递归过的数字,放入“备忘录”,当再次要递归该数的时候,直接从备忘录来取即可,这就是所谓的记忆化搜索。
- 添加一个备忘录
- 递归返回时,将结果放入备忘录
- 进入递归时,检查备忘录是否有
class Solution {
public:int memo[31];int fib(int n){//-1不可能出现在备忘录当中, 设为初始值memset(memo, -1, sizeof(memo));return dfs(n);}int dfs(int n){if(memo[n] != -1){return memo[n];}if(n == 0 || n == 1){memo[n] = n; //返回之前将结果放入备忘录return n;}memo[n] = dfs(n-1) + dfs(n-2);return memo[n];}
};
动态规划
动态规划,五步走:
- 确定状态表示(dfs函数的含义)
- 推导状态转移方程(dfs函数体)
- 初始化(dfs函数递归出口)
- 确定填表顺序(填写备忘录顺序)
- 确定返回值(主函数如何调用dfs)
这五步和上面的记忆化搜索能一一对应起来,因为它们本质都是一样的,都将已经计算的值存起来
class Solution {
public:int dp[31];int fib(int n){dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};
62. 不同路径
题目链接:62. 不同路径 - 力扣(LeetCode)
递归(暴搜)
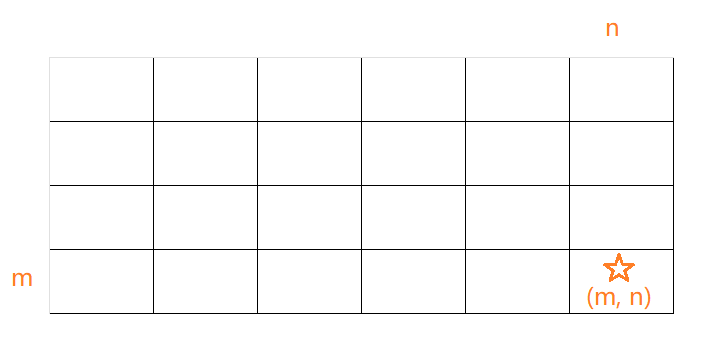
交给dfs到达(i, j)有多少种方法,这题就是到达(m, n)有多少种方法,函数头即是:dfs(m, n)
假设要到达菱形这个位置,只需要知道到达两个绿圆圈有多少种方法即可,因为只有必须要通过这两个位置,即dfs(i-1, j) + dfs(i, j-1)

将起点设置为(1, 1)更方便遍历,那么当i == 0 || j == 0的时候,无需递归;
(1, 1)为起点,也无需递归,即这两个就是出口。
class Solution {
public:int uniquePaths(int m, int n){return dfs(m, n);}int dfs(int i, int j){if(i == 0 || j == 0){return 0;}if(i == 1 && j == 1){return 1;}return dfs(i-1, j) + dfs(i, j-1);}
};
暴搜会超时
记忆化搜索
这里递归展开,也会出现很多重复的,所以可以将暴搜转换成记忆化搜索:
- 定义一个“备忘录”
- 递归前检查“备忘录”
- 返回之前将结果存入“备忘录”
class Solution {
public:int uniquePaths(int m, int n){vector<vector<int>> memo(m+1, vector<int>(n+1));return dfs(m, n, memo);}int dfs(int i, int j, vector<vector<int>>& memo){if(memo[i][j] != 0){return memo[i][j];}if(i == 0 || j == 0){return 0;}if(i == 1 && j == 1){memo[i][j] = 1;return 1;}memo[i][j] = dfs(i-1, j, memo) + dfs(i, j-1, memo);return memo[i][j];}
};
动态规划
就是将递归版本改为迭代版本
class Solution {
public:int uniquePaths(int m, int n){vector<vector<int>> dp(m+1, vector<int>(n+1));dp[1][1] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(i == 1 && j == 1){continue;}dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};
300. 最长递增子序列
题目链接:300. 最长递增子序列 - 力扣(LeetCode)
递归
直接暴力枚举所有递增子序列,然后选出里面最长的
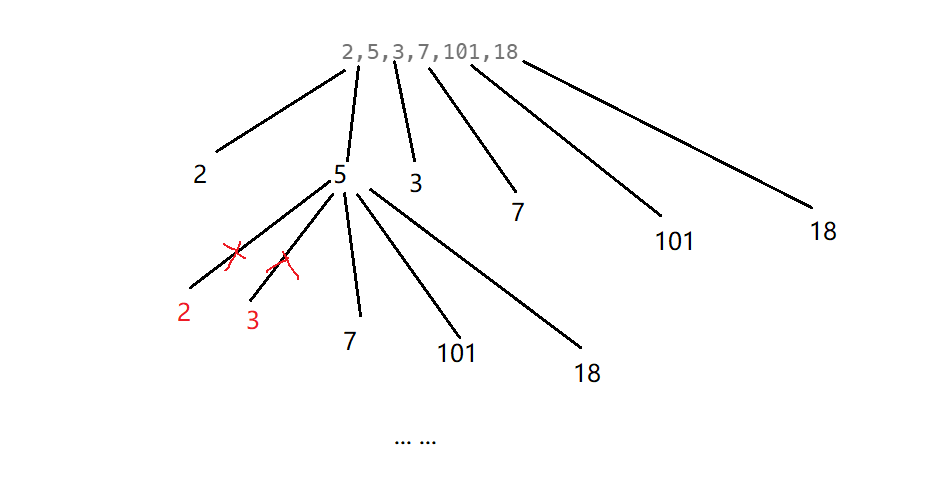
代码解释:
- 不知道是哪个起点的子序列最长,一次for循环
- 递归函数,以当前位置为头,寻找下一个位置的子序列,一次for循环
- 无需设置出口处,因为有for循环,遍历结束自动出来了
class Solution {
public:int lengthOfLIS(vector<int>& nums){int ret = 0;for(int i = 0; i < nums.size(); i++){ret = max(ret, dfs(i, nums));}return ret;}int dfs(int pos, vector<int>& nums){//要算自己int ret = 1;for(int i = pos+1; i < nums.size(); i++){if(nums[i] > nums[pos]){ret = max(ret, dfs(i, nums) + 1);}}return ret;}
};
会超时,多叉树
记忆化搜索
上图可见,递归的时候,会出现重复元素的递归,所有可以采用记忆化搜索的方式
class Solution {
public:int lengthOfLIS(vector<int>& nums){int ret = 0;vector<int> memo(nums.size(), 0);for(int i = 0; i < nums.size(); i++){ret = max(ret, dfs(i, nums, memo));}return ret;}int dfs(int pos, vector<int>& nums, vector<int>& memo){if(memo[pos] != 0){return memo[pos];}//要算自己int ret = 1;for(int i = pos+1; i < nums.size(); i++){if(nums[i] > nums[pos]){ret = max(ret, dfs(i, nums, memo) + 1);}}memo[pos] = ret;return ret;}
};
动态规划
dp表的含义:以某个位置为起点的最长递增子序列的长度- 求
pos位置的时候,依赖的是pos后面的值,所以填表顺序是从后往前填 - 要算上自己,所以初始的值为
1
class Solution {
public:int lengthOfLIS(vector<int>& nums){int n = nums.size();vector<int> dp(n, 1);int ret = 0;for(int i = n-1; i >= 0; i--){for(int j = i+1; j < n; j++){if(nums[j] > nums[i]){dp[i] = max(dp[i], dp[j]+1);}}ret = max(ret, dp[i]);}return ret;}
};