目录

牛客_五子棋（判断是否有赢）

解析代码

---

牛客_五子棋（判断是否有赢）

五子棋__牛客网

题目：

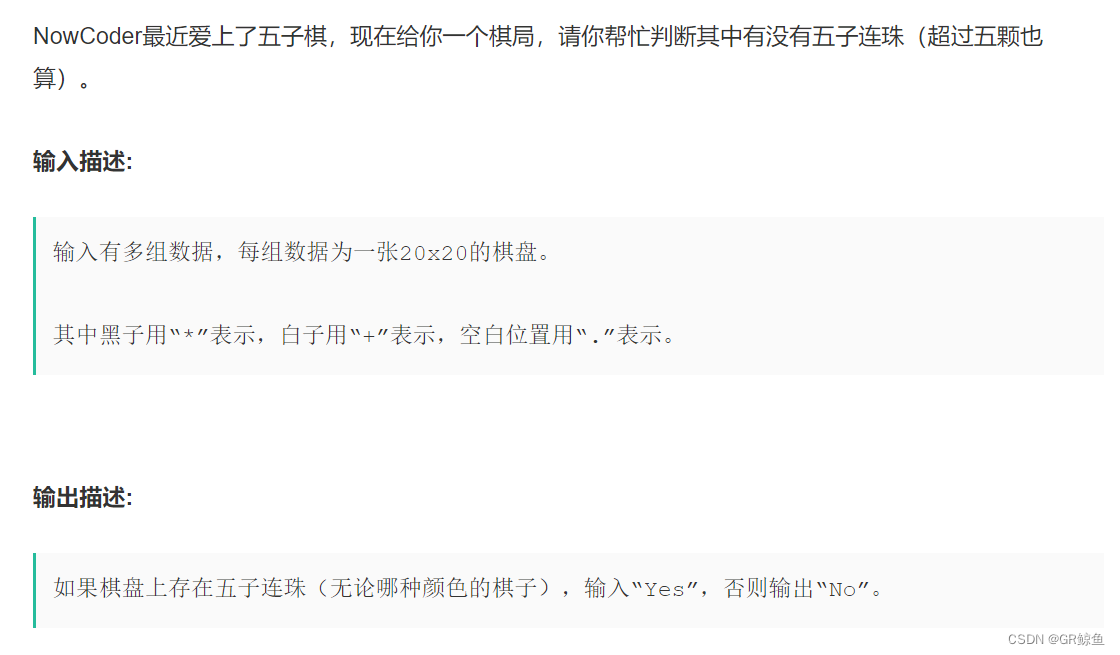
用例输入：

....................
....................
....................
....................
......*.............
.......*............
........*...........
....++++.*..........
..........*.........
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
.......*............
......+*+++.........
.......*............
.......*............
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................

用例输出：

Yes
No

---

解析代码

        dir代表当前位置的8个方向，其中上下、左右、左上右下、右上左下为必须放在一起检测。

获取一个棋盘，按照行列检测棋盘中的每个位置，当拿到一个位置后，按照以下步骤操作：

1. 以该位置为中心，依次检测该位置的上下、左右、左上右下、右上左下，比如左上
2. 从该位置开始向上检测，找出连在一起的同种棋子个数，再向下检测同种棋子的个数并累计，注意在检测时，中心位置统计了两次，上下统计完时，需要给结果减去1
3. 按照2统计完上下、左右、左上右下、右上左下各个方向，找出最大的同种棋子个数
4. 检测3中统计出的最大同种棋子个数，如果大于等于5，输出YSE，否则取下一个位置继续1
5. 如果所有的位置检测完，没有超过5个的相同棋子，则输出NO

#include <iostream>
#include <vector>
#include <string>
using namespace std;
#define N 20int count(vector<string> table, char ch, int x, int y)
{int maxc = 0;int dir[4][2][2] = { {{ -1,0 },{ 1,0 }},{{ 0,-1 },{ 0,1 }},{{ -1,-1 },{ 1,1 }},{{ -1,1 },{ 1,-1 }} };for (int i = 0; i < 4; ++i) // 四种方向{int c = 0;for (int j = 0; j < 2; ++j) // 两个小方向{int nx = x, ny = y;while (nx >= 0 && nx < N && ny >= 0 && ny < N && table[nx][ny] == ch){nx += dir[i][j][0];ny += dir[i][j][1];++c;}}maxc = (maxc > c ? maxc : c);}return maxc - 1; //统计两个方向（如横向的左右两个方向）的时候，当前棋子被计算了两次
}bool solve(vector<string> table)
{// 遍历棋谱，如果某个位置有棋子，再向该位置进行搜索for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){if (table[i][j] == '*' || table[i][j] == '+')if (count(table, table[i][j], i, j) >= 5)return true; // 当某个位置有连在一起的棋子，结束搜索}}return false;
}int main()
{vector<string> table(N);while (cin >> table[0]){for (int i = 1; i < N; ++i){cin >> table[i];}cout << (solve(table) ? "Yes" : "No") << endl;}return 0;
}