图结构在多个领域中扮演着重要角色，它能有效地模拟实体间的连接关系，通过从图中提取有意义的特征，可以获得宝贵的信息提升机器学习算法的性能。

本文将介绍如何利用NetworkX在不同层面（节点、边和整体图）提取重要的图特征。

本文将以NetworkX库中提供的Zachary网络作为示例。这个广为人知的数据集代表了一个大学空手道俱乐部的社交网络，是理解图特征提取的理想起点。

我们先定义一些辅助函数来设置图的可视化选项。以下代码中包含两个函数，一个用于实现颜色映射，另一个用于定义默认的节点属性。

 defcreate_color_map():  # 定义颜色映射的颜色（从蓝色到橙色）colors= ["#002049", "#FFA500"]  # 蓝色到橙色  # 创建颜色映射  returnmcolors.LinearSegmentedColormap.from_list("blue_orange_cmap", colors)  defset_default_node_options():  return {  'node_color': '#4986e8',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }

下面的函数有助于根据不同的可视化选项绘制图的节点、边和相关标签。通过这种实现，我们可以灵活地根据需求调整图元素的特征。

 # 绘图函数  defdraw_graph(G, pos, node_options=None, edge_options=None, node_labels=None, edge_labels=None):  # 绘制节点  ifnotnode_options:  node_options=set_default_node_options()  nx.draw_networkx_nodes(G, pos, **node_options)  # 绘制节点标签  ifnotnode_labels:  node_labels=set_default_node_labels()  nx.draw_networkx_labels(G, pos, **node_labels)  # 绘制边  ifnotedge_options:  edge_options=set_default_edge_options()  nx.draw_networkx_edges(G, pos, **edge_options)  # 绘制边标签  ifedge_labels:  nx.draw_networkx_edge_labels(G, pos, **edge_labels)  # 显示图  plt.axis('off')  plt.gca().set_aspect('equal')  plt.show()

让我们使用这些辅助函数来可视化Zachary数据集。

 G=nx.karate_club_graph()  pos=nx.spring_layout(G, iterations=10, seed=20000)  draw_graph(G, pos)

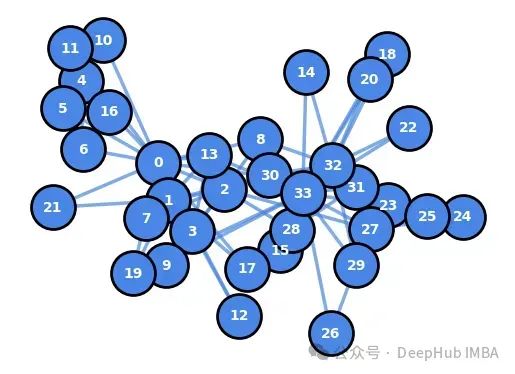
基于这个图，我们将深入探讨NetworkX的功能，以提取基于节点、基于边和基于图的特征。

基于节点的特征

基于节点的特征是与图中单个节点相关的属性。这些特征对于各种图分析任务至关重要，包括节点分类、链接预测和社区检测，因为它们提供了关于单个节点在网络结构中角色的信息。以下是一些基于节点的特征示例。

节点度

节点度指的是连接到一个节点的边的数量。在社交网络的context中，用户的节点度对应于他们在平台上的连接数。具有高节点度的用户可以被视为网络中更具社交活跃性的个体，类似于拥有众多粉丝的社交媒体影响者。

具有低节点度的用户连接较少，类似于在平台上拥有小范围朋友圈的用户。在这种情况下，理解节点度可以帮助识别关键用户、分析社交结构，并为用户engagement策略提供信息。

 dg=dict(G.degree())  node_options=set_options_for_centrality(G, dg.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

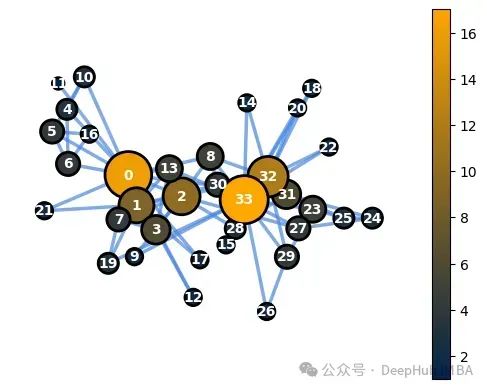
我们可以计算网络的平均节点度，以了解每个节点平均连接的边数。

 num_edges=G.number_of_edges()  num_nodes=G.number_of_nodes()  avg_degree=0  avg_degree=round(2*num_edges/num_nodes)  print("边数:", num_edges, "节点数:", num_nodes)  print("空手道俱乐部网络的平均度为 {}".format(avg_degree))

 边数: 78 节点数: 34空手道俱乐部网络的平均度为 5

节点度中心性

节点度中心性是衡量节点在网络中重要性的指标，基于其连接数量。虽然节点度直接计算连接数量，但节点度中心性将这个值标准化为网络中可能的总连接数。这种标准化使得我们能够在不同规模的网络中对节点进行更有意义的比较。

比如说在交通网络中，节点度中心性可以帮助识别关键的枢纽或交叉点。具有高度中心性的机场将连接到许多其他机场，这表明它在交通网络中扮演着中心枢纽的角色。这个度量是基于网络规模进行标准化的，允许我们对不同地区或国家的机场进行有意义的比较。

 dc=nx.degree_centrality(G)  node_options=set_options_for_centrality(G, dc.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

上图为我们这个数据集的节点度中心性

特征向量中心性

特征向量中心性是衡量节点在网络中影响力的指标。它为所有节点分配分数，高分节点的连接比与低分节点的同等连接贡献更多。

为了理解特征向量中心性的核心原理，让我们考虑一个学术引用网络的例子。假设A教授发表了5篇论文，每篇被1或2篇引用次数较少的其他论文引用。B教授发表了3篇论文，每篇都被引用次数达数百的高影响力论文引用。尽管A教授的发表数量更多，但B教授的特征向量中心性可能更高，因为他们的工作被更有影响力的论文引用。

这个指标在理解复杂网络中的影响力和信息流动方面特别有用，例如引用或合作网络。在这种情况下，特征向量中心性可以帮助识别某个领域的关键影响者和开创性工作，即使它们可能没有最高的原始引用计数。

 ec=nx.eigenvector_centrality(G)  node_options=set_options_for_centrality(G, ec.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

上图为特征向量中心性

介数中心性

介数中心性是一个重要的图论概念，它量化了一个节点在其他节点对之间最短路径上充当桥梁的频率。如果一个节点经常位于连接其他节点对的最短路径上，那么它就具有高介数中心性。

为了更直观地理解这个概念，我们可以考虑一个公司的通信网络。想象一个大型公司中的中层管理者。这个管理者可能具有高介数中心性，因为他在高层管理和各个部门之间传递信息，促进不直接互动的员工之间的沟通，并作为公司范围内倡议的桥梁。

如果这个中层管理者离职可能会显著影响信息流，这样就突显了其在公司通信网络中的关键角色（以介数中心性衡量）。

介数中心性特征的代码：

 bc=nx.betweenness_centrality(G)  node_options=set_options_for_centrality(G, bc.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

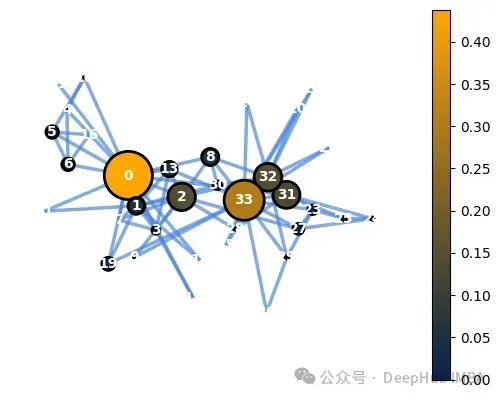
接近中心性

接近中心性评估一个节点与网络中所有其他节点的接近程度。具有高接近中心性的节点可以通过较少的跳跃快速到达网络中的其他节点。

为了更好地理解这个概念，我们可以想象一个城市的地铁系统，其中车站是节点，铁路连接是边。一个"中央车站"直接连接到许多其他车站，而几个边缘车站只连接到一两个附近的车站。

在这个网络中，"中央车站"会有高接近中心性，因为它可以快速到达大多数其他站，通常只需一个直接连接或单次转乘。这使得"中央车站"成为高效穿越城市的理想点，也适合快速在整个网络中传播信息（如服务更新）。边缘车站的接近中心性较低，因为乘客需要多次转乘才能从这些车站到达网络的其他部分。

在这种情况下，接近中心性对于理解交通网络的效率和结构至关重要，可以帮助城市规划者优化路线并识别关键枢纽。

接近中心性特征的代码：

 ce=nx.closeness_centrality(G)  node_options=set_options_for_centrality(G, ce.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

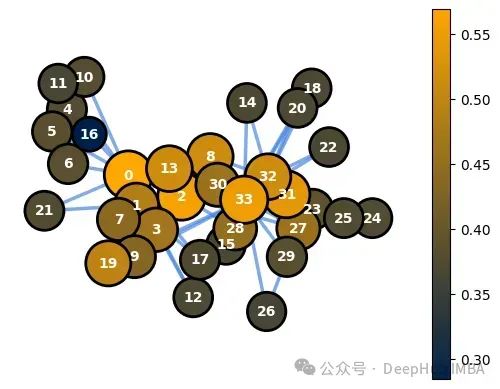
聚类系数

聚类系数是一个量化图中节点聚集程度的重要指标。它反映了一个节点的两个邻居也是彼此邻居的可能性。

与关注节点在整个网络中的重要性或影响力的节点中心性度量不同，聚类系数提供了关于节点周围局部结构的洞察。

为了更好地理解这个概念，我们考虑蛋白质相互作用网络中的三个蛋白质：A、B和C。

蛋白质A与其他10个蛋白质相互作用，但这些蛋白质之间没有相互作用。其聚类系数将为0。

蛋白质B与其他10个蛋白质相互作用，而且这些蛋白质也都相互作用。其聚类系数将为1。

蛋白质C与其他10个蛋白质相互作用，其中5对蛋白质相互作用。其聚类系数值将在0和1之间，具体取决于其邻近蛋白质之间的确切相互作用数量。

在这种情况下，即使代表蛋白质的节点具有相同数量的连接，聚类系数也可以揭示生物系统中不同的局部网络结构。

可视化聚类系数特征的代码：

 cc=nx.clustering(G)  node_options=set_options_for_centrality(G, cc.values(), set_default_node_options())  draw_graph(G, pos, node_options=node_options)

比较中心性值

比较不同的中心性值对网络分析非常有帮助，因为它提供了对节点在网络中角色的全面理解。以下是主要原因：

多维视角：不同的中心性度量捕捉了节点影响力的各个方面。例如度中心性显示直接连接，而特征向量中心性考虑这些连接的质量。

识别关键节点：通过比较中心性值，可以识别重要节点。例如一个具有高介数中心性的节点可能对维持网络连通性至关重要，即使它可能没有最高的节点度中心性。

细致分析：比较中心性可以揭示细微的洞察。例如一个节点可能连接到许多重要节点（高特征向量中心性），但可能不是最接近所有其他节点的（较低的接近中心性）。

网络结构洞察：中心性度量的差异可以突显网络的结构特征。例如度中心性和介数中心性之间的差异可能表明存在桥接节点或瓶颈。

以下是用Pandas可视化和生成数据框架的代码，用于比较网络中检测到的节点中心性值。

 importpandasaspd  data= [dc, ec, bc, ce]  indices= ['Degree Centrality', 'Eigenvector Centrality', 'Betweenness Centrality', 'Closeness Centrality']df=pd.DataFrame(data, index=indices).T  df.style.background_gradient(cmap=create_color_map())

比较网络中一些节点的中心性值，这些值揭示了这个社区中不同成员的具体角色。根据表1中报告的结果，我们可以比较例如两个最关键的节点，节点0和节点33。

节点0基于中心性值的特征：

联系广泛：它在俱乐部中有广泛的联系，类似于一个认识大多数其他成员的资深成员。

关键连接点：它对连接不同子群体至关重要，类似于一个连接各种技能水平或年龄组的教练。

高效沟通者：它与其他成员有效沟通，类似于一个能快速传播活动或日程变更信息的俱乐部组织者。

节点33基于中心性值的特征（与节点0相比）：

更多直接连接：它的连接略多于节点0，如一个与大多数成员互动的俱乐部主席或主教练。

高影响力连接：它连接到稍微更有影响力的成员，类似于认识一群长期练习者的核心群体的人。

较低的整体连通性：它对整体连通性不那么重要，像一个受人尊敬的成员，但不一定促进不同群体之间的沟通。

这些指标突显了节点0和33的不同角色。虽然节点33有更强的局部连接，但节点0对俱乐部的整体结构和信息流动更为关键。

其他节点扮演完全不同的角色。例如节点16的中心性度量值非常低。其他情况如节点19，则表现出不同的值。

节点16基于中心性值的特征：

极少连接：它的连接很少，主要是与不太中心的成员连接，像一个只参加过几次课的新学员。

无桥接作用：它从不充当其他成员之间的桥梁，类似于还没有参与任何俱乐部社交活动的人。

边缘位置：它与网络中的大多数其他节点距离较远，类似于很少参加课程或在训练课程之外与他人互动的成员。

与节点33和0不同，节点16的影响力最小，对俱乐部的社交结构或信息流动没有显著贡献。

节点19基于中心性值的特征：

有限直接连接：它的直接连接很少，像一个只认识少数其他练习者的新成员。

部分高影响力连接：它与一些有影响力的成员有一些连接，类似于与几个高级学员或教练有过互动的初学者。

较少桥接作用：它很少充当桥梁，类似于不经常在俱乐部的不同群体之间促成介绍的成员。

中等接近度：它与其他成员的距离适中，像是可以通过共同认识的人联系到大多数俱乐部成员的人。

这些值表明节点19在网络中处于边缘位置，像是空手道俱乐部中一个较新或不太活跃的成员。尽管直接连接和影响力有限，但与节点16相比节点19仍然与更中心的成员保持一些联系。

基于边的特征

基于边的特征是从图中节点之间的关系中派生出来的特征，而不是单个节点的属性。这些特征捕捉了网络结构和连接模式的信息。

基于距离的特征（最短路径）

在图分析中，基于距离的特征用于衡量网络中节点对之间的邻近度或距离。为了更好地理解这些特征背后的核心概念，我们可以考虑一个全球航空网络的例子，其中机场是节点，航线是边。

基于距离的特征可以帮助识别两个机场之间的最短路径。例如找到从纽约到东京中转次数最少的最有效路线。这种分析可以帮助航空公司优化他们的航班连接，同时也使乘客能够更好地规划他们的行程。

对于航空公司等实体而言，基于距离的特征至关重要，它们可以据此做出关于路线规划、机场发展和提高整体航空运输网络效率的战略决策。

可视化两个节点之间最短路径的代码：

 # 识别最短路径  path=nx.shortest_path(G, source=21, target=22)  path_edges=list(zip(path,path[1:]))  node_options=set_default_node_options()  # 绘制并高亮节点和边  nx.draw(G, pos, node_color='black', node_size=500)  node_options= {  'nodelist': path,  'node_color': '#4986e8',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }  edge_options= {  'edgelist': path_edges,  'edge_color': '#4986e8',  'width': 5,  'alpha': 0.7,  }  draw_graph(G, pos, node_options=node_options, edge_options=edge_options)

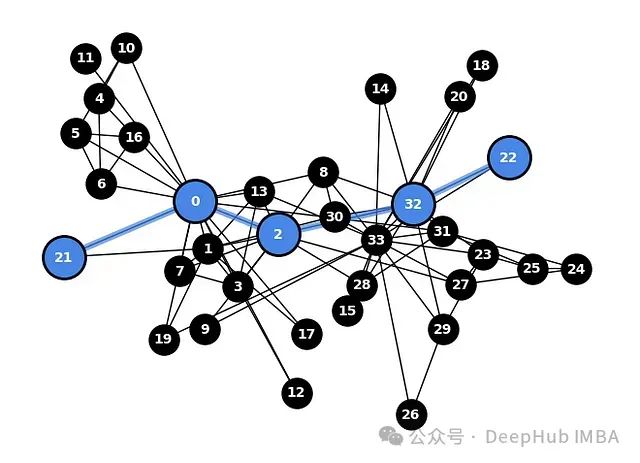
局部邻域重叠

局部邻域重叠是一个衡量图中两个节点共享共同邻居程度的指标。它通过计算两个节点邻居节点的交集来量化这两个节点之间的相似度。

为了更好地理解这个概念，我们可以考虑一个社交网络的例子。假设Alice是Charlie、David和Emma的朋友，Bob是David、Emma和Frank的朋友。在这种情况下，Alice和Bob之间的局部邻域重叠将是他们的共同朋友，即David和Emma。这种重叠表明Alice和Bob有相似的社交圈，即使他们可能没有直接连接。

可视化两个节点之间局部邻域重叠的代码：

 # 识别共同的局部邻居  loc_neigh=sorted(nx.common_neighbors(G, 32, 33))  # 绘制并高亮选定的节点  nx.draw(G, pos, node_color='k', node_size=500)  selected_options= {  'nodelist': [32, 33],  'node_color': 'orange',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }  nx.draw_networkx_nodes(G, pos, **selected_options)  # 绘制并高亮邻居  node_options= {  'nodelist': loc_neigh,  'node_color': '#4986e8',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }  draw_graph(G, pos, node_options=node_options)

全局邻域重叠

全局邻域重叠是一个衡量图中两个节点扩展邻域之间相似度的指标。它计算在一定距离内（通常是2或更多跳）共同邻居与该距离内总的不同邻居的比例。

与局部邻域重叠仅限于直接连接不同，全局邻域重叠捕捉了更广泛的网络模式。这使得全局邻域重叠特别适用于理解网络结构中的长程相似性。

为了说明这个概念可以考虑研究人员的合作网络：

局部邻域重叠可能识别出经常合著论文的两个研究人员，表明他们密切合作或在同一研究小组中。

全局邻域重叠可能揭示来自不同机构的两个研究人员，虽然没有直接合作，但有相似的扩展合作者网络。这可能表明他们在同一领域工作或有相似的研究兴趣，尽管地理上相距甚远。

中可视化两个节点之间全局邻域重叠的代码，突出显示了它们的邻居之间的相关路径：

 # 检测局部邻域重叠  edges= []  nodes= []  paths=nx.all_simple_paths(G, source=0, target=3, cutoff=3)  forpinpaths:  nodes.append(p)  edge=list(zip(p, p[1:]))  edges.append(edge)  # 节点和边的扁平化列表  nodes= [  x  forxsinnodes  forxinxs  ]  edges= [  x  forxsinedges  forxinxs  ]  # 绘制图的基本元素  nx.draw(G, pos, node_color='k', node_size=500)  # 绘制源节点和目标节点  selected_options= {  'nodelist': [0, 3],  'node_color': 'orange',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }  nx.draw_networkx_nodes(G, pos, **selected_options)  # 绘制全局邻居节点及其与源节点和目标节点的相关连接  node_options= {  'nodelist': [nforninnodesifnnotin [0, 3]],  'node_color': '#4986e8',  'node_size': 1000,  'edgecolors': 'black',  'linewidths': 2,  }  edge_options= {  'edgelist': edges,  'edge_color': '#4986e8',  'width': 5,  'alpha': 0.7,  }  draw_graph(G, pos, node_options=node_options, edge_options=edge_options)

基于图的特征

基于图的特征是从图的整体结构和属性中派生出来的特征，而不是从单个节点或边中派生的。这些特征捕捉了整个网络拓扑的信息，可以提供对图中全局模式的洞察。以下是一些基于图的特征示例。

Graphlets（从节点到图特征的角度）

Graphlets是在较大图中检测到的小型子图，代表局部连接模式。Graphlets可以从两个角度来理解：作为节点特征和图特征。

作为节点特征：Graphlets可以用于表征单个节点周围的局部邻域结构。通过检查一个节点参与的Graphlets可以获得关于其在网络中局部连接模式的信息。

作为图特征：Graphlets也可以描述图的整体结构。通过计算整个图中不同Graphlets的出现次数可以获得图拓扑的"指纹"。

Graphlets在网络分析中具有多方面的应用价值：

分类任务：可以从每个节点的邻域中提取基于Graphlet的特征，并用作机器学习模型的输入，以预测节点标签或类别。

网络比较：基于Graphlet频率的相似性度量可以用于比较或分组不同的网络。

结构分析：Graphlets捕捉了贡献于形成局部分组模式的特定节点排列，提供了关于网络结构的深入洞察。

以下是可视化NetworkX中提供的Atlas中所有连接图（最多6个节点）的非同构Graphlets的代码：

 importrandom  GraphMatcher=nx.isomorphism.vf2userfunc.GraphMatcher  defatlas6():  Atlas=nx.graph_atlas_g()[3:209]  # 0, 1, 2 => 没有边。208是最后一个6节点图  U=nx.Graph()  forGinAtlas:  ifnx.number_connected_components(G) ==1:  ifnotGraphMatcher(U, G).subgraph_is_isomorphic():  U=nx.disjoint_union(U, G)  returnU  G_atlas=atlas6()  plt.figure(1, figsize=(6, 6))  pos=nx.nx_agraph.graphviz_layout(G_atlas, prog="neato")  C= (G_atlas.subgraph(c) forcinnx.connected_components(G_atlas))  forginC:  c= ['#4986e8'] *nx.number_of_nodes(g)  # 随机颜色...  nx.draw(g, pos=pos, node_size=40, node_color=c, vmin=0.0, vmax=1.0, with_labels=False)  plt.show()

Weisfeiler-Leman特征

Weisfeiler-Leman (WL)特征源自WL算法，这是一种用于测试图同构的迭代方法。这些特征通过迭代更新节点标签（基于相邻节点的标签）来捕捉图的结构信息。WL特征在图分析任务中特别有用，例如图分类，因为它们提供了一种将图结构编码为特征向量的方法，可以被机器学习算法有效利用。

以下代码演示了如何使用WL特征。我们创建一个与网络同构的新图G_perm。然后在两个图上运行WL算法以生成代表WL图特征的哈希值：

 importnetworkxasnx  importnumpyasnp  fromnetworkx.algorithmsimportisomorphism  # 获取G1的邻接矩阵  adj_matrix=nx.to_numpy_array(G)  # 创建节点的随机置换  n=G.number_of_nodes()  np.random.seed(42)  permutation=np.random.permutation(n)  # 创建置换矩阵  P=np.zeros((n, n))  foriinrange(n):  P[i, permutation[i]] =1  # 将置换应用于邻接矩阵：P*A*P^T  permuted_adj_matrix=P@adj_matrix@P.T  # 从置换后的邻接矩阵创建置换图  G_perm=nx.from_numpy_array(permuted_adj_matrix)  # 检查图是否同构  iso_check=isomorphism.is_isomorphic(G, G_perm)  print(f"G和G_perm是否同构？{iso_check}")  # 计算两个图的Weisfeiler-Lehman图哈希  hash_G=nx.weisfeiler_lehman_graph_hash(G)  hash_G_perm=nx.weisfeiler_lehman_graph_hash(G_perm)  # 打印哈希值  print(f"G的Weisfeiler-Lehman图哈希：{hash_G}")  print(f"G_perm的Weisfeiler-Lehman图哈希：{hash_G_perm}")  # 比较哈希值  are_hashes_equal=hash_G==hash_G_perm  print(f"G和G_perm的WL图哈希是否相等？{are_hashes_equal}")

结果如下：

 G和G_perm是否同构？True  G的Weisfeiler-Lehman图哈希：c7184009df3be2e402cfcb318efaa4b3  G_perm的Weisfeiler-Lehman图哈希：c7184009df3be2e402cfcb318efaa4b3  G和G_perm的WL图哈希是否相等？True

通过利用WL算法可以分配特定的图特征，使我们能够理解G（对应于我们的图数据）和G_perm（对应于G的置换）具有相同的关系结构。以下图表显示了G和G_perm的节点度特征。

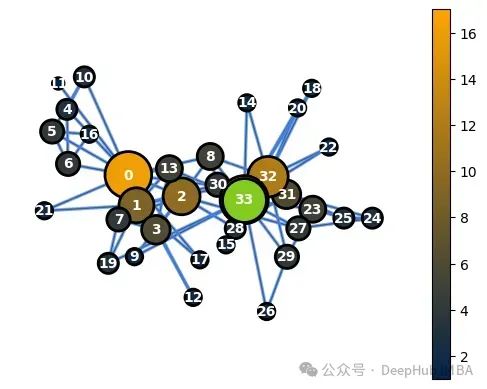
G中的节点度值（高亮显示节点33）

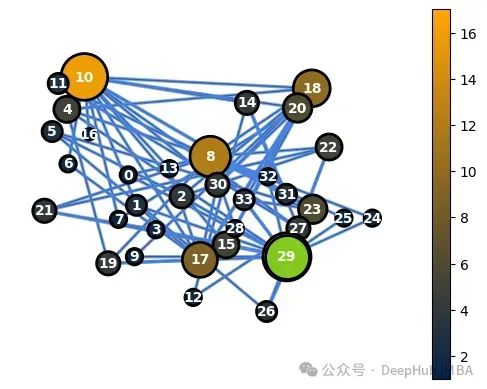
G_perm中的节点度值（高亮显示节点29）

G中的节点33在置换过程后对应于G_perm中的节点29。这两个节点将具有相同的基于节点和基于边的特征。要识别两个图之间对应节点的对，可以运行以下代码，替换我们感兴趣的节点id：

 node_id=33  permuted_node_id=np.where(permutation==33)[0][0]

总结

本文深入探讨了从网络结构中提取的三个主要特征类别：

1. 基于节点的特征：这些特征提供了网络中个体实体的信息。
2. 基于边的特征：这些特征捕捉了关系和连接模式的重要信息。
3. 基于图的特征：这些特征提供了整体网络拓扑的更高层次视角。

通过综合利用这些不同类型的特征，可以够获得对网络结构的全面理解，识别关键参与者，分析信息流动模式，并发现潜在的隐藏模式。

以Zachary的网络数据集为例，我们展示了如何应用这些特征来揭示俱乐部内的潜在角色和联系。值得注意的是，这些特征提取和分析方法不仅限于社交网络，还可以广泛应用于其他领域，如交通网络分析和生物系统研究。

通过本文介绍的方法和技术，研究者和数据科学家可以更有效地分析复杂网络，从而在各个领域中获得更深入的洞察和更准确的预测。

https://avoid.overfit.cn/post/1feaf07255eb4ee4bfcf10512c158b0b

作者：Giuseppe Futia