算法分享——《双指针》

文章目录

✅[《移动零》](https://leetcode.cn/problems/move-zeroes/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
✅[《复写零》](https://leetcode.cn/problems/duplicate-zeros/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
- - 🧛‍♀️复写操作：
  - 🚲查找最后一位：
✅[《快乐数》](https://leetcode.cn/problems/happy-number/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
- - 🍗扩展（鸽巢原理）：
✅[《盛最多水的容器》](https://leetcode.cn/problems/container-with-most-water/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
✅[《有限三角形的个数》](https://leetcode.cn/problems/valid-triangle-number/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
✅[《两数之和 II - 输入有序数组》](https://leetcode.cn/problems/kLl5u1/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
✅[《三数之和》](https://leetcode.cn/problems/3sum/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：
- - 🚁双指针遍历：
  - ⚓去重操作：
✅[《四数之和》](https://leetcode.cn/problems/4sum/description/)
- 🌹题目描述：
- 🚗代码实现：
- 😴代码解析：

✅《移动零》

🌹题目描述：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

🚗代码实现：

class Solution {
public:void moveZeroes(vector<int>& nums) {int dest = -1, cur = 0;while(cur < nums.size()){if(nums[cur] != 0) swap(nums[++dest], nums[cur++]); // 处理非0元素else cur++;}}
};

😴代码解析：

本次代码的思路与我们在学习排序所了解到的快速排序原理类似。
在快排中，最重要的思路是**区域划分。本次题目也是这样。

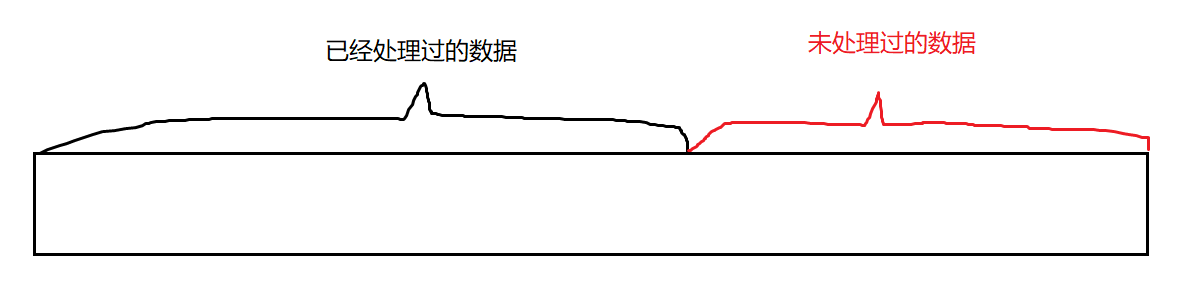
对于该题目来说，最后的目标是使得全部0在数组后面，那我们想要实现该操作肯定是需要去遍历整个数组。
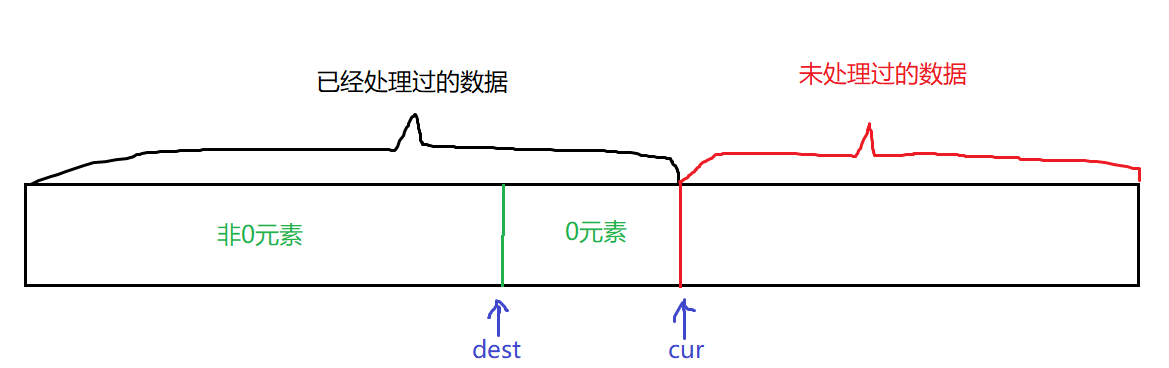
那么遍历也会有被遍历处理过的数据和未被遍历处理的数据**。这种情况我们的做法一般是对一个数组进行区域划分。

对于解决区域划分问题，我们可以使用双指针算法。要么我们定义一个left或一个right，也可以是cur或一个dest。
是否记得我们在学习数据结构中，对于带环链表的题解中，我们有用到过快慢指针，其实那也是一种双指针的算法。

通过题目要求，我们是需要不改变非0元素的排列顺序，只是将全部0元素放在数组末尾。而通过区域划分，我们又可以对已处理过的数据进行区域划分。

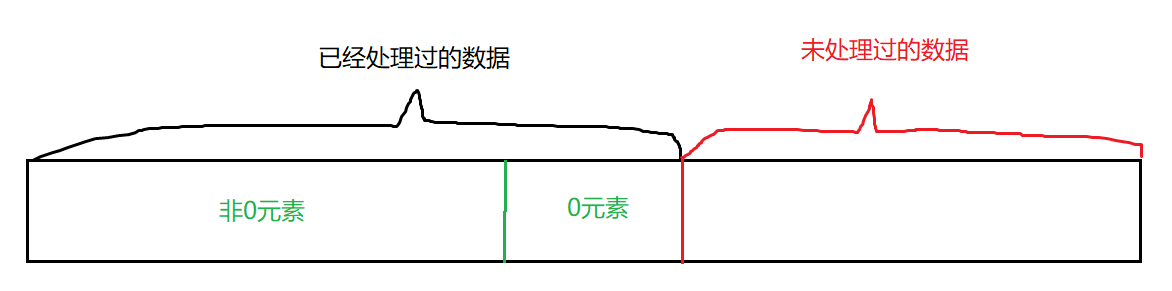
那么为了遍历整个数组，首先我们需要定义一个cur指针来进行遍历判断数据，再然后通过dest指针来实现区域划分，用来标记区域划分位置。

cur的作用：从左向右扫描数据，遍历数组
dest的作用：在已处理的区间内，指向非0元素的最后一个位置（实现区域划分）

所以对应的区域划分就为：
[0, dest] ——> 非0元素
[dest + 1, cur - 1] ——> 0元素
[cur, size() - 1] ——> 未处理的数据

下面我们就来看看代码是如何实现的：

首先关于dest和cur的定义，由于dest均为非0元素，并且也是处理过的数据，因此我们刚开始初始化的时候需要将dest设置为-1.
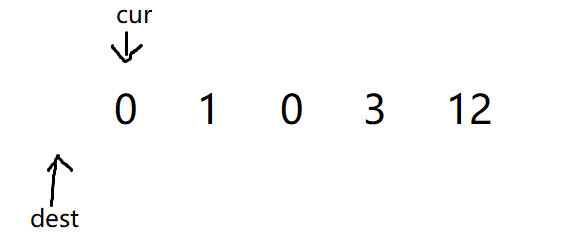
接下来在cur指向0的时候，因为要满足已处理的数据满足前部分为非0元素，后部分为0元素，所以我们只需要将cur继续遍历，这样0元素就是已经处理过的数据，也满足了[dest + 1, cur - 1]为0元素
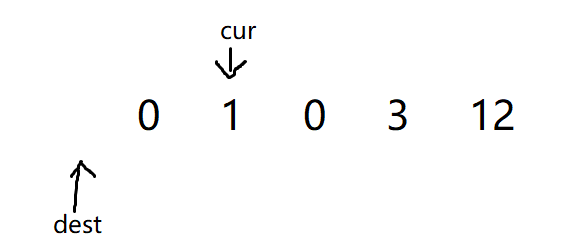
如果遇到cur指向不为0时，只需要将dest往后走一格再与cur指向的值进行交换，随后cur再往后挪动一格。同样也满足区域划分，
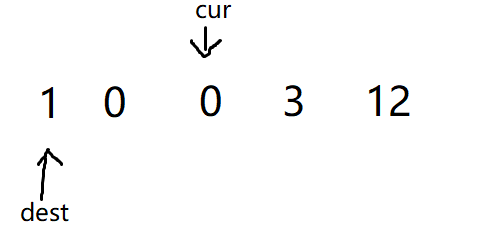
再然后又遇到0，所以cur再往后挪动一格，指向3时再++dest和cur交换，随后cur再往后一格

—————————————————————————————————
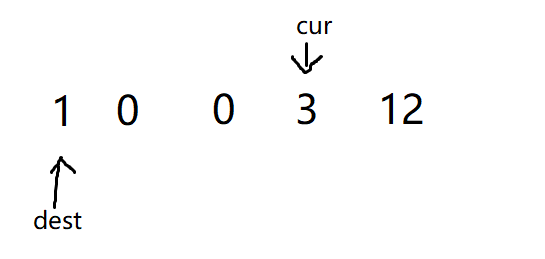
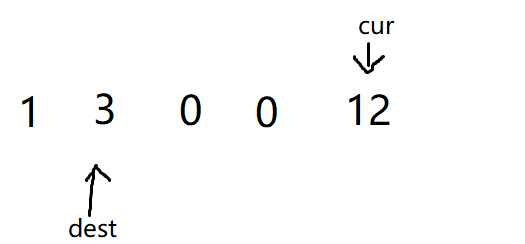
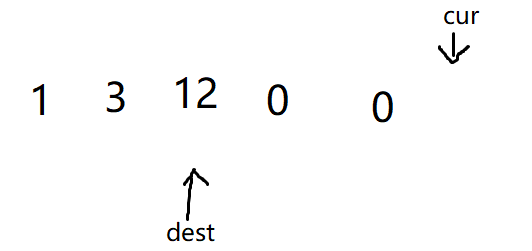
随后再按照上述步骤进行交换，就能得到正确结果：

✅《复写零》

🌹题目描述：

给你一个长度固定的整数数组 arr ，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。

注意：请不要在超过该数组长度的位置写入元素。请对输入的数组就地进行上述修改，不要从函数返回任何东西。

示例 1：

输入：arr = [1,0,2,3,0,4,5,0]
输出：[1,0,0,2,3,0,0,4]
解释：调用函数后，输入的数组将被修改为：[1,0,0,2,3,0,0,4]

示例 2：

输入：arr = [1,2,3]
输出：[1,2,3]
解释：调用函数后，输入的数组将被修改为：[1,2,3]

🚗代码实现：

class Solution
{
public:void duplicateZeros(vector<int>& arr) {int n = arr.size();int flag = 0;int dest = 0;while (dest < n){if (arr[dest] == 0){flag += 2;}else{++flag;}if (flag >= n) break;dest++;}int cur = n - 1;if (flag > n){arr[cur--] = 0;dest--;}// 复写操作while (cur >= 0){if(arr[dest] == 0){arr[cur] = arr[dest];cur--;}arr[cur--] = arr[dest--];}}
};

😴代码解析：

对于这道题目，如果说可以新开辟一块数组供我们使用的话，是很容易想的也很容易实现。可是现在难就难如何在原地实现呢？

我们一开始可以试试正向遍历，但是这个方法很快就走不通了，因为我们会覆盖掉本来存在的数据，导致后面就全部都是错的。

所以正向的思路走不通，我们可以”掉头“试试。我们从反向进行遍历：

🧛‍♀️复写操作：

如果是要从反向开始遍历，我们就需要先找到答案中最后一个数是多少，就比如示例1中的答案的最后一个数字是4，因此我们可以将dest先放在4原数组的4上，然后将cur放在最后一个数字上，开始从后向前遍历
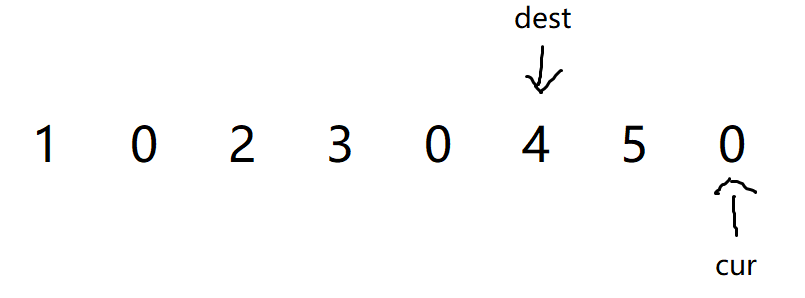
先将判断dest指向的数据是否为0，此时dest指向的数据是4，然后将dest指向的数据覆盖掉cur指向的数据
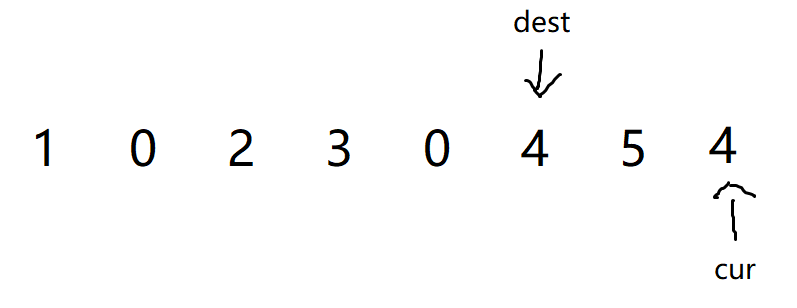
再将cur--，dest也进行--操作
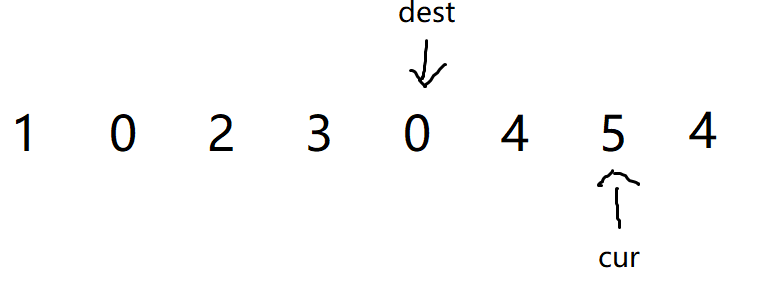
此时dest指向的数据为0，那么cur要把指向的数据覆盖为0，并且把前一个数据也覆盖为0，cur总共要将自己指向的值覆盖两次。然后cur--还有dest--
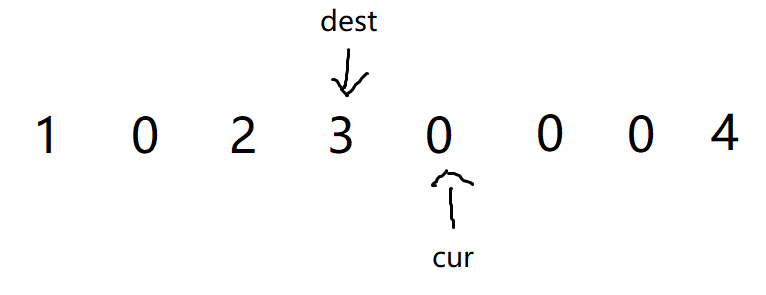
随后继续进行，dest指向的不为0，所以将cur指向的数据进行覆盖为dest指向的数据
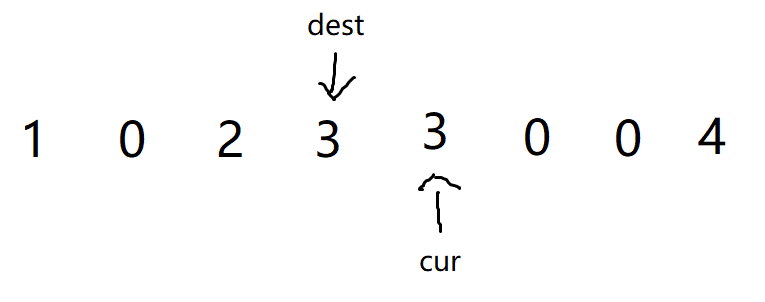
再进行--操作
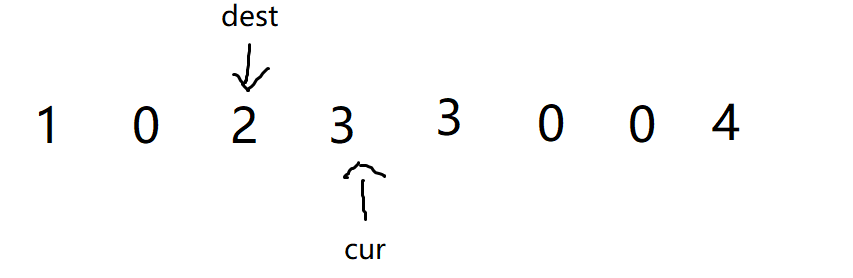
同理，直接覆盖再进行--
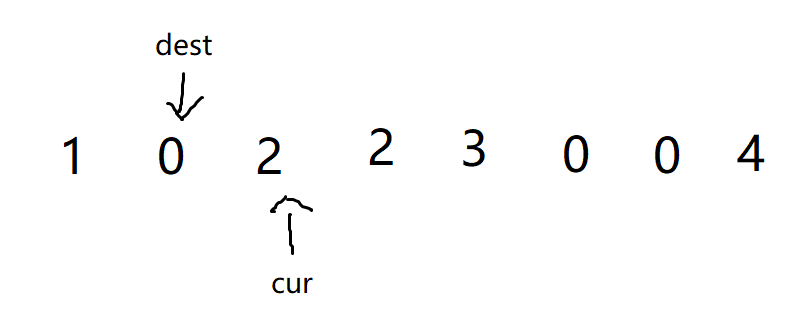
此时dest指向的数据又为0，因此覆盖掉cur指向的数据和cur前一个的数据
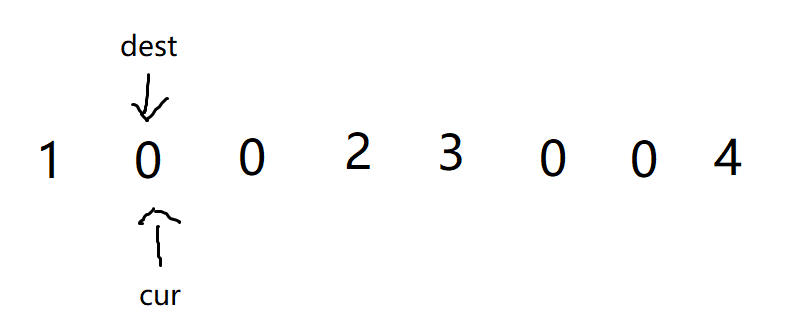
继续同时进行--操作
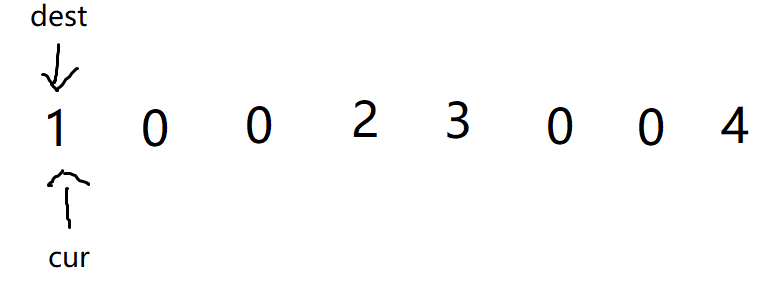
再覆盖

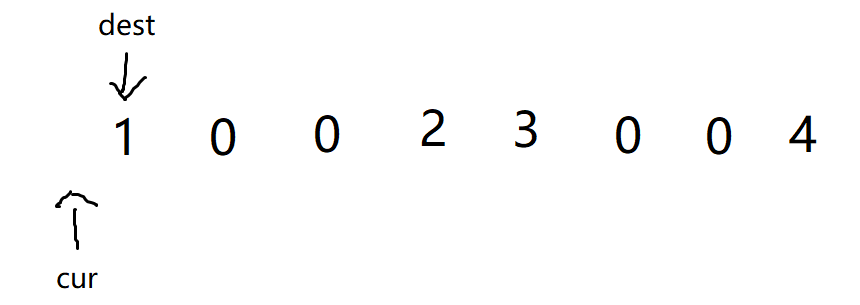
至此复写操作结束，结果也和答案一致。

先判断 dest 位置的值
决定 cur 向前移动一步还是两步
判断一下 cur 是否已经结束为止
dest–

🚲查找最后一位：

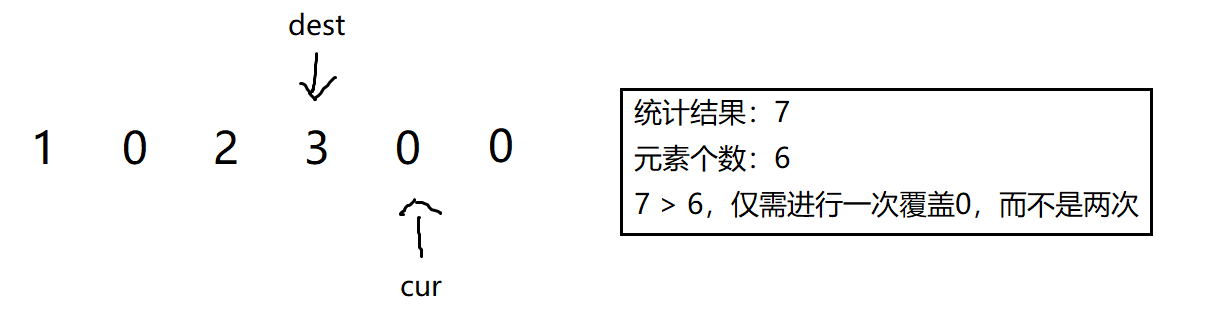
上述的操作，代表我们已经掌握了本题的解法，但是我们是通过答案知道复写完之后的最后一位的数字结果是4，但我们又该如何不通过答案找到数字呢？

其实我们如果用最原始的方法也是可以的，就是先计算数组有多少个元素，再通过数0的个数再乘2就可以找出那个所谓的最后一个数。

例如在示例1中，我们先遍历数组，访问到非0元素就+1，遇到0元素就+2，然后统计起来。
如果统计的结果 == 数组元素的个数。
那我们就找到了dest的，也就是复写完数组中的最后一个数。

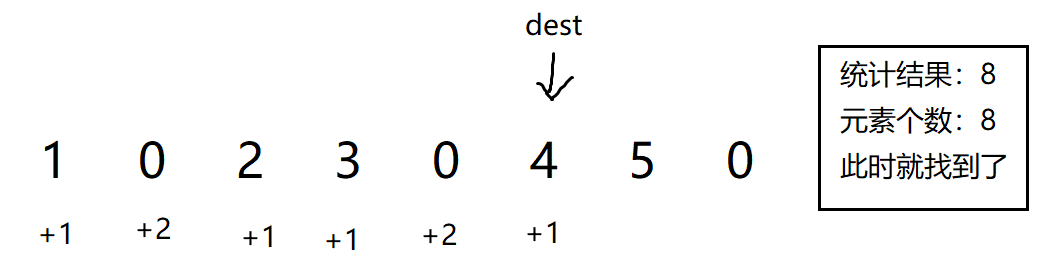
这样我们就可以再定义一个cur指针指向最后一个元素，继续正常实现上述的复写操作就可以了。

[!WARNING]

但是我们还会遇到一种情况，需要特别注意拿来讨论：

此时我们在实现复写操作的时候，必须要进行一次判断，如果统计结果 > 元素个数，就需要先将最后一个元素替换为0，然后dest和cur再同时--，以这时候的状态为基准继续执行上述的复写操作：

✅《快乐数》

🌹题目描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1

示例 2：

输入：n = 2
输出：false

🚗代码实现：

class Solution 
{
public:int func(int n){int sum = 0;while(n){sum += (n % 10) * (n % 10);n /= 10;}return sum;}bool isHappy(int n) {int slow = n;int fast = func(n);while(fast != slow){slow = func(slow);fast = func(func(fast));}return slow == 1;}};

😴代码解析：

我们刚拿到该题目的时候可以尝试画图，当我们在画图的过程中，我们就会发现这个图像非常像我们之前所讲解的一种题型：

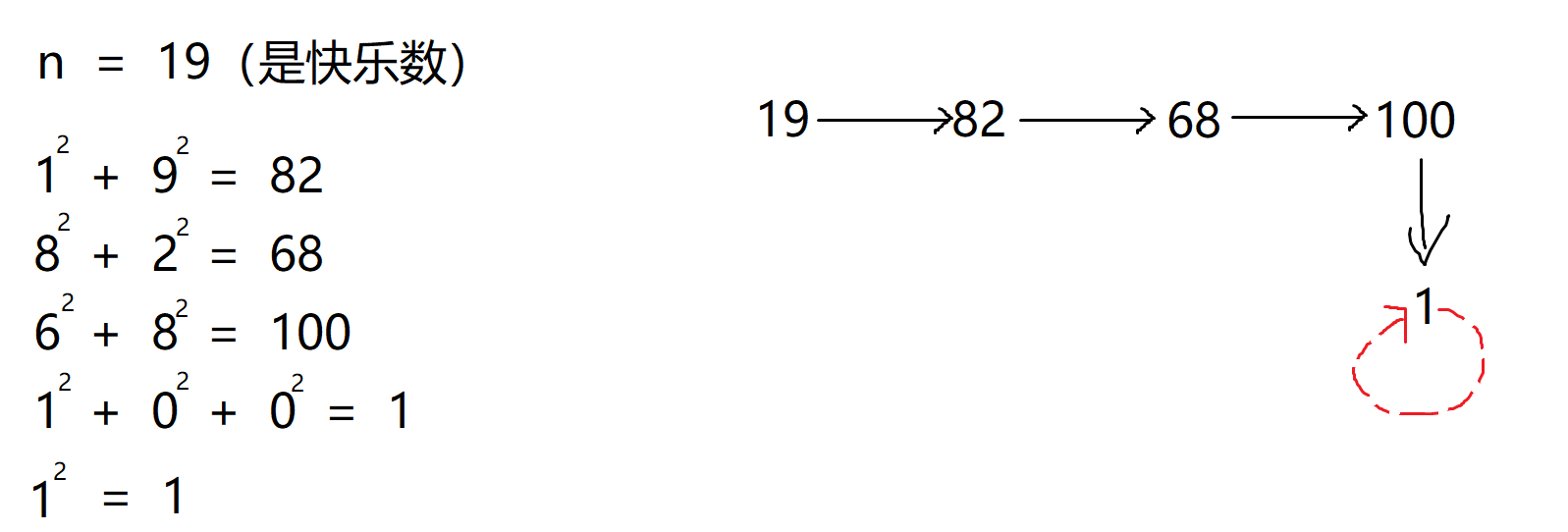
上述我所想解释的是，当作为一个快乐数，如果一直不断计算下去，它的答案会一直为1，所以会一直在1进行循环。可能目前还不能彻底回忆起我们之前讲解的提醒，那我们再来看看非快乐数是怎么样的：

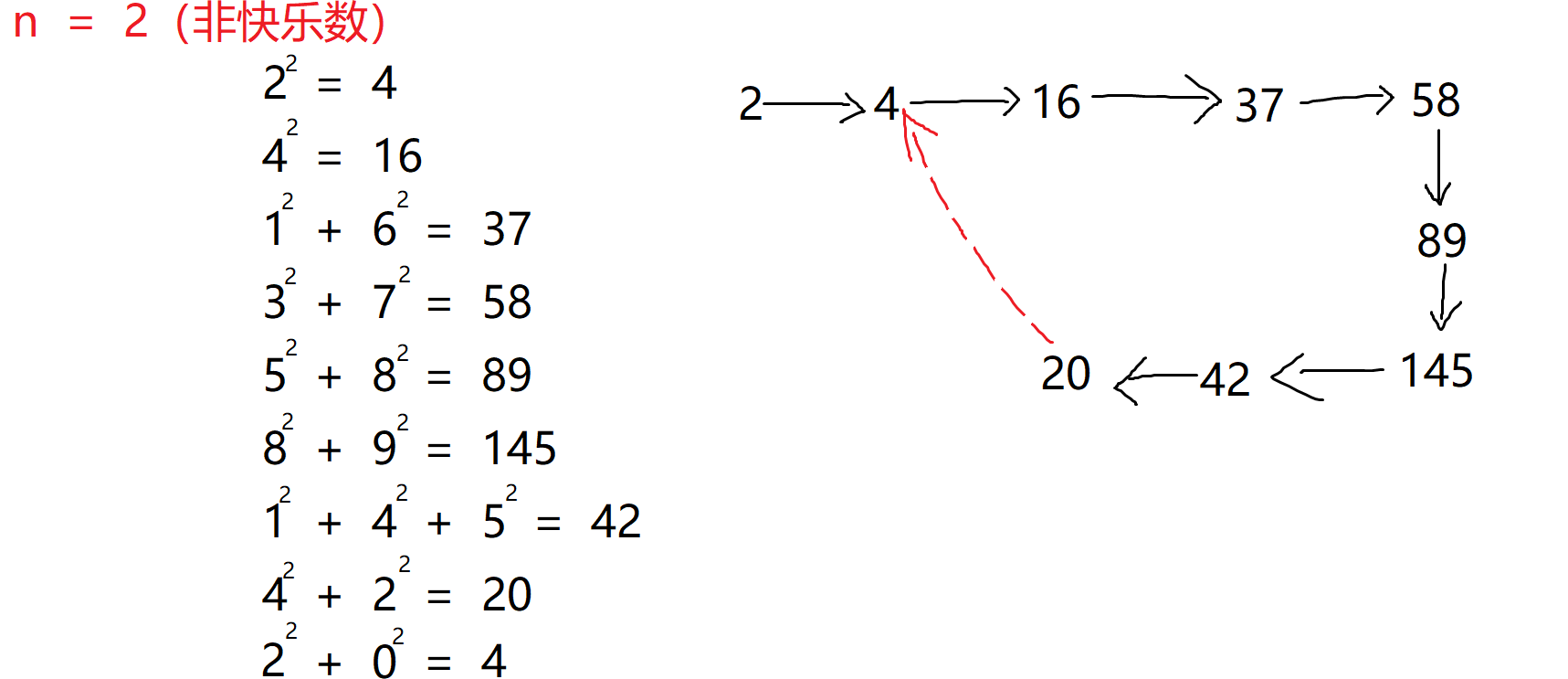
诶，是不是有点感觉了？是不是特别像我们以前在学习数据结构链表的一道OJ题，题目是“判断是否为环形链表”呢？对于判断成环问题，我们用的算法就是——快慢指针。如果你清楚可以看看我的博客：链表OJ

所以现在我们就清楚了，具体快慢指针的算法我就不在这里赘述了。

我们只要**判断它们相遇的时候，当前的值是多少就可以。**判断是不是快乐数了

但是不同于链表，我们这里要额外实现一个函数，用来计算各位的平方和并且得出结果。这如同是一个快慢指针的转换，同逻辑但不同形式。

🍗扩展（鸽巢原理）：

我们在这里仅仅是介绍了两种情况，但有没有一种情况是一只无限循环下去，不形成环的情况呢？

在这里我可以先总结：不存在不成环的情况！

具体的证明我们可以用鸽巢原理来证明。首先我们需要先简答了解一下鸽巢原理：

假设有 n 个巢穴和 n+1 个鸽子，如果要将这 n+1 个鸽子分配完并且这 n 个巢穴都分满，则一定会保证有一个巢穴中的鸽子数一定大于1

那么对于该题目来说，就算是一个无符号整形，它的最大取值是4294967295。差不多说是4.2 * 10^9.假设我现在要将无符号整形的范围扩大，扩大到9999999999，也就是9 * 10^9，那么这个 9 * 10^9进行上述的函数操作号，得到的结果就是 9^2 * 10 = 810，所以你夸张扩大后的值最大也就810。也就是说你的4294967295之内的全部数字，不管怎么样都是只能在810之内的，也就是[1, 810]。

此时这个[1, 810]这810个数字就是“巢穴”，若是现在我们进行了811此操作，而且又存在一个数字很好运，将810个数字全部填满，那么再进行下一次操作时，它一定也会在这个[1, 810]之中，所以会出现重复的数！因此这就是为什么一定**不存在不成环的情况！**

✅《盛最多水的容器》

🌹题目描述：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

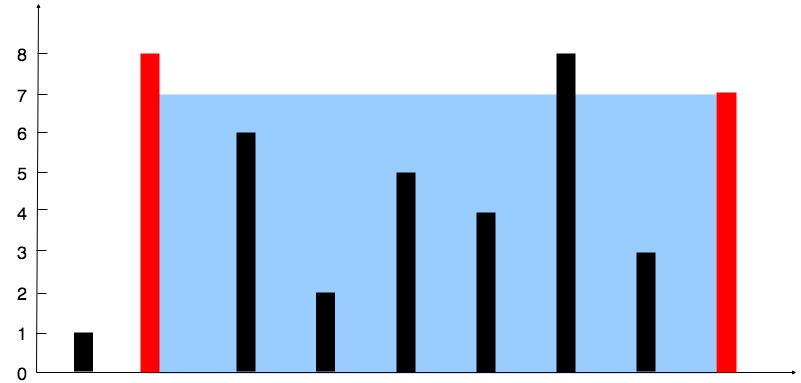
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

🚗代码实现：

class Solution 
{
public:int maxArea(vector<int>& height) {int V = 0;int left = 0, right = height.size() - 1;while(left < right){V = max(V, (right - left) * min(height[left], height[right]));if(height[left] < height[right]) left++;else right--;}return V;}
};

😴代码解析：

该题目就是我们从小到大经常听到的“木桶原理”的变形，题目也很好理解。我们需要不断的比较底和高的数值，最终来实现比较体积的大小。

当然，我们可以使用暴力解法，直接不断枚举进行比较，但是时间复杂度就是O(N^2)了，所以肯定不推荐。那么目前又是对应着一个“数组”，因此我们可以采取双指针的思路。

我们可以在0位置处定义一个左指针left，在最后的位置定义右指针right即可。然后在判断的时候，让当前对应的高度较小的下标进行++ 或 – 操作，直到两指针相遇，这样就使得时间复杂度为O(N)。

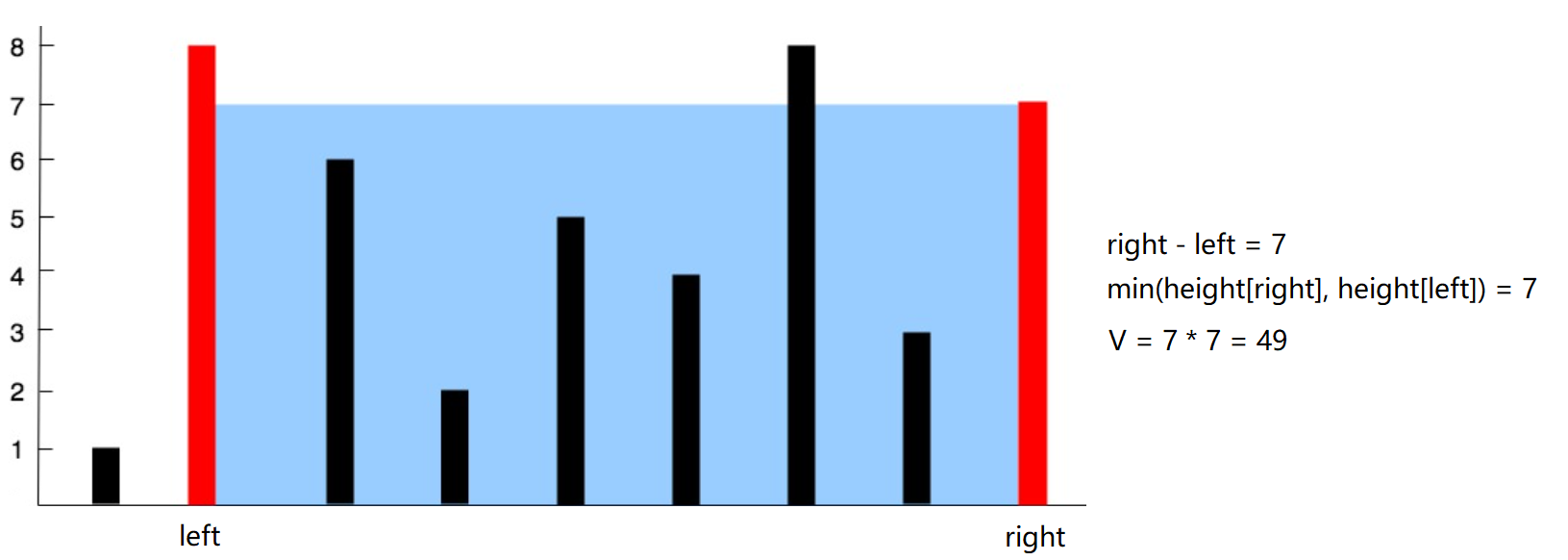
因为height[right]所对应的高度小，所以让right-- 去左边找合适的值，但是也会伴随着“底”长度的减少：

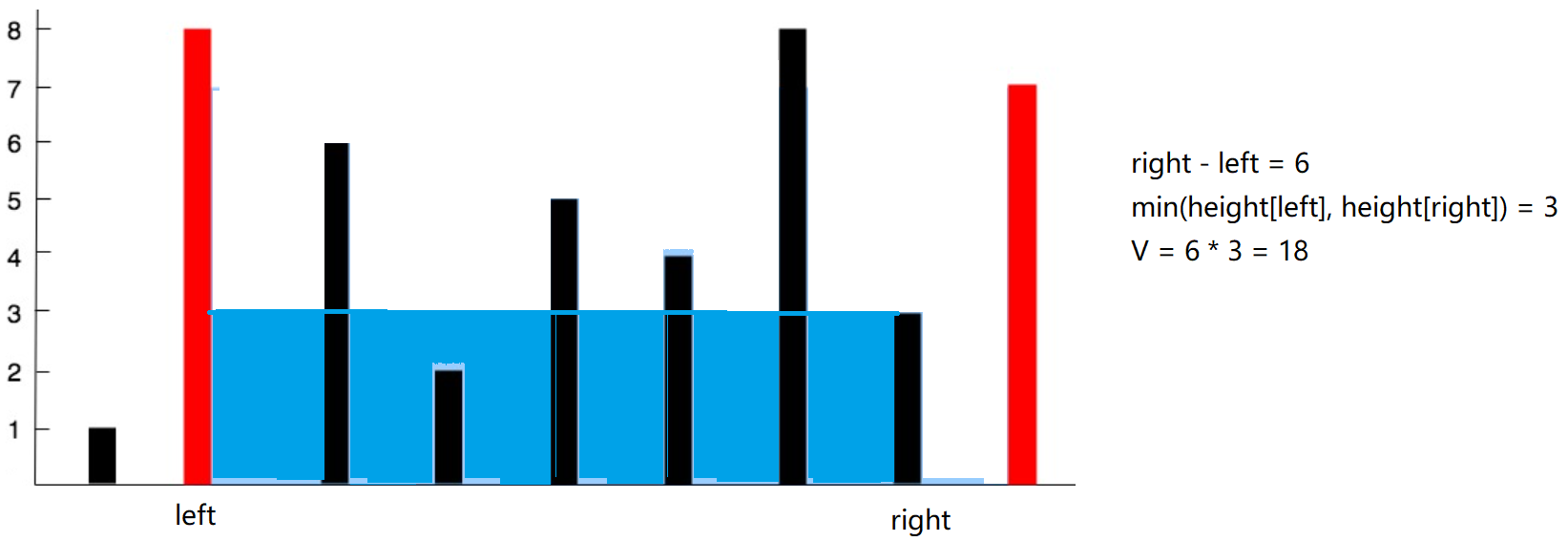
所以我们只需要不断 ++ 和 --就好，然后每次比较V的最大值，并保留最大值即可。

✅《有限三角形的个数》

🌹题目描述：

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

输入: nums = [4,2,3,4]
输出: 4

🚗代码实现：

class Solution 
{
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int sum = 0， flag = nums.size() - 1;while(flag > 1){int left = 0, right = flag - 1;while(left != right){if(nums[left] + nums[right] > nums[flag]){sum += (right - left); // 精华所在--right;}else ++left;}--flag;}return sum;}
};

😴代码解析：

我们在上小学的时候就知道，一个三角形的构成条件，一定是满足存在任意两条边 > 第三条边（即 a + b > c），这样才能组成一个三角形。

对于这道题当然也有暴力解法，就是一遍一遍进行排列组合进行比对，但是这样时间复杂度高，效率低下。因此我们需要换一种思路来思考。

仔细想一想，对于该道题我们又是在一段数组上进行操作，那么毫无疑问——“双指针”。但是一开始的数据是乱序的，如果我们一上来就进行比较就会毫无章法，毫无逻辑。因此我们需要做好前置工作，先排序！
因此我们可以使用 C++的sort函数来进行排序，在参数里面传入vector的迭代器，begin( ) 和 end( )

这样我们排完序之后，代码就变得直观可看了，数组也具有==单调性==了，以下我们会对数组的单调性来展开：

首先，排完序后，最右边的数肯定是最大的，而最左边的数就是最小的。
不妨先判断最小的数字，加上中间的数字中的某个数字，才能做到大于最大的数？
找到中间的某个数A，发现A能做到加上最左边的数能够大于最右边的数，我们就可以得出，从A下标到起始位置的下标对应的全部数，加上A下标对应的数，肯定大于整个数组最大的那个数。下面我们就来证明这个结论

下面我们拿数据 nums = [2, 2, 3, 4, 5, 6] 来进行讲解：

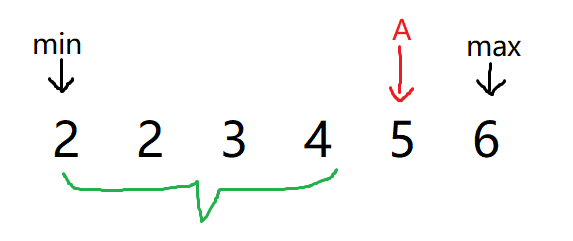
如图所示，对于一个已经排完序的数组，最左边一定是最小的数而最右边一定是最大的数，这时我们找到了一个数A，我们发现A加上min是大于max的，所以由于数组是有序的，因此min和A之间的全部数都大于 min，所以既然min加上A都可以大于max，所以中间的也全部都可以。

但是我们仔细看看，其实3 4 5这三个数也可以组成一个三角形，所以我们的A数要不断移动的，max同时也要移动，所以我们就可以利用单调性的双指针转化为：

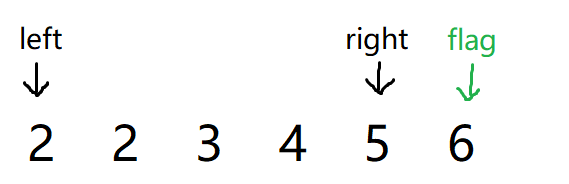
flag：作为标记位，代表着三角形中最长的边
left：作为数组中最小的值，代表着三角形中最短的边
right：最为重要的值，代表着三角形中合适的数与left相加大于flag，初始化时在flag左边一位方便遍历全部数据

刚刚我们讲了，这种情况下right 到 left之间的全部数都满足。
接下来我们需要将right往左，因为right右边的值肯定大于当前的right的值，所以往右走肯定可以满足构成三角形，所以我们right往左走。看看还有没有与之匹配的三角形。

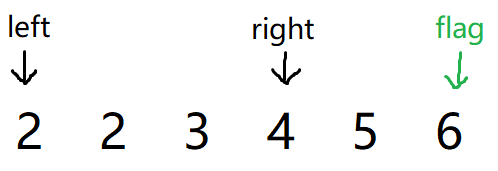
这个时候就nums[left] + nums[right] == nums[flag]，不能组成三角形，因此最有可能的原因就是left小了，看看还有没有大一点的值加上nums[right]可以大于nums[flag]的，所以left向右移动

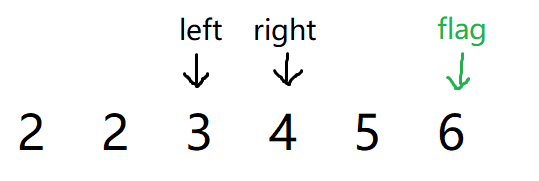
这个时候就正好满足三角形，但是随后right移动后两指针相遇了，我们就结束循环了。

但是还没有完，我们还需要让flag向左移动，因为可能还有满足最长边为5的，并且其它两条边加起来大于5的边，因此我们还需要继续判断，同时还要重置 left 和 right 的值。

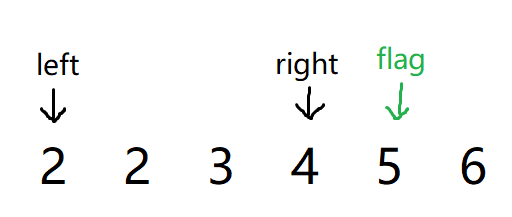
至此再不断重复前面的操作即可！！！

a + b > c ——> right - left, right–
a + b <= c ——> left++

✅《两数之和 II - 输入有序数组》

🌹题目描述：

给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值*。*numbers 的下标 从 0 开始计数 ，所以答案数组应当满足 0 <= answer[0] < answer[1] < numbers.length 。

假设数组中存在且只存在一对符合条件的数字，同时一个数字不能使用两次。

示例 1：

输入：numbers = [1,2,4,6,10], target = 8
输出：[1,3]
解释：2 与 6 之和等于目标数 8 。因此 index1 = 1, index2 = 3 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[0,2]

示例 3：

输入：numbers = [-1,0], target = -1
输出：[0,1]

🚗代码实现：

class Solution 
{
public:vector<int> twoSum(vector<int>& numbers, int target) {int left = 0, right = numbers.size() - 1;while(left != right){if(numbers[left] + numbers[right] > target) --right;else if(numbers[left] + numbers[right] < target) ++left;else return {left, right};}return {-1, -1}; // 照顾编译器，随便写数据即可}
};

😴代码解析：

该题目和上面《有限三角形的个数》相似，两道题都是利用排序好的数组的单调性来进行判断，我们也很容易就能得出该题的解法——”双指针“。

我们可以在最左边和最右边定义两个指针，用来向左向右遍历，判断条件也很简单：

numbers[left] + numbers[right] > target 这个时候由于有序数组的单调性，仅需要先将right进行减减操作
numbers[left] + numbers[right] < target 这个时候由于有序数组的单调性，仅需要先将left进行加加操作
numbers[left] + numbers[right] == target 这个时候就找到了对应的下标，然后利用vector的隐式类型转换返回即可。

✅《三数之和》

🌹题目描述：

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

🚗代码实现：

class Solution
{
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vv;sort(nums.begin(), nums.end());int flag = nums.size() - 1;// 如果nums[flag] < 0，那nums[left]和nums[right]也都小于0，这样相加就没意义了while(flag > 1 && nums[flag] >= 0) { int target = 0 - nums[flag], left = 0, right = flag - 1;while(left < right) // 一定是要 left < right 可不能 left != right，这样会造成left > right{if(nums[left] + nums[right] > target) --right;else if(nums[left] + nums[right] < target) ++left;     else{vv.push_back({nums[left], nums[right], nums[flag]});// 找到数据后还要继续遍历！left++, right--;while(left < flag && nums[left] == nums[left - 1]) ++left;while(right >= 0 && nums[right] == nums[right + 1]) --right;}}--flag;// 一定要避免越界while(flag > 1 && nums[flag] == nums[flag + 1]) --flag;}return vv;}
};

😴代码解析：

区别于前面的《两数之和》，本题目有特别多的细节问题需要我们来处理，因为本题目不再是要求遇到满足的就返回，而是将全部满足的结果存放至vector容器中，再返回，而且存储答案的容器中还不能有重复的答案。

如果以暴力的角度来看，我们当然可以定义三个指针一个一个值进行比对，然后将匹配的三个值存放在vector中，再接着我们可以用set容器来进行去重操作。说实话利用set容器进行去重这还好说，但是你直接暴力的话，这个算法还是有些挫的。

所以我们完全可以像上述《两数之和》和《有限三角形的个数》那样先排序成满足单调性的数组，再利用双指针进行遍历，这样的算法不仅时间复杂度低，效率也高，而且我们也可以不用set容器就可以完成去重的操作！但是针对于去重操作，这一点尤为难受，如果你刚拿到这道题想的就是双指针 + 不用set来操作，那你一上手就会出现很多细节问题，诸如越界啦，甚至说right指针跑到left指针左边去了等等，所以接下来我们来展开好好说一说！

🚁双指针遍历：

该算法的实现和《有限三角形的个数》算法一样，先将数组进行排序，再定义left 和 right指针，用来遍历，定义flag来标记最后一个值，然后判断nums[left] + nums[right] 是否等于nums[flag]。

但是本题目不一样，我们要找到满足nums[left] + nums[right] + nums[flag] == 0的全部值，这种我们也可以转化成nums[left] + nums[right] == -nums[flag]然后剩下的内容就和《有限三角形的个数》解法一样了。

⚓去重操作：

首先我们来分析问题，我们就拿题目给的例子然后进行排序再修改下数据，往里添加几个0和1：

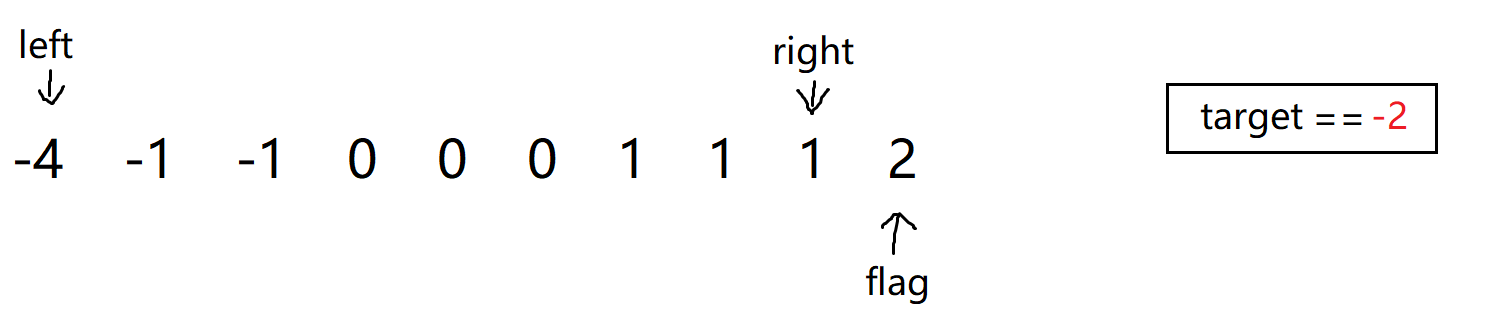
和前面讲过的题目一样，只是我们这里是要让nums[left] + nums[right] == -nums[flag]即可，为了方便我们在这里定义target == -nums[flag]。
1、nums[left] + nums[right] < target就让left++
2、nums[left] + nums[right] > target就让right--
3、nums[left] + nums[right] == target就让各个值push_back到答案容器vector中
这些就是基本双指针判断了，我也不细讲了，我们主要是来讲解去重操作：

由图可知，此时的各个值满足nums[left] + nums[right] < target（-4 + 1 < -2），所以我们需要将left++，然后再继续判断：
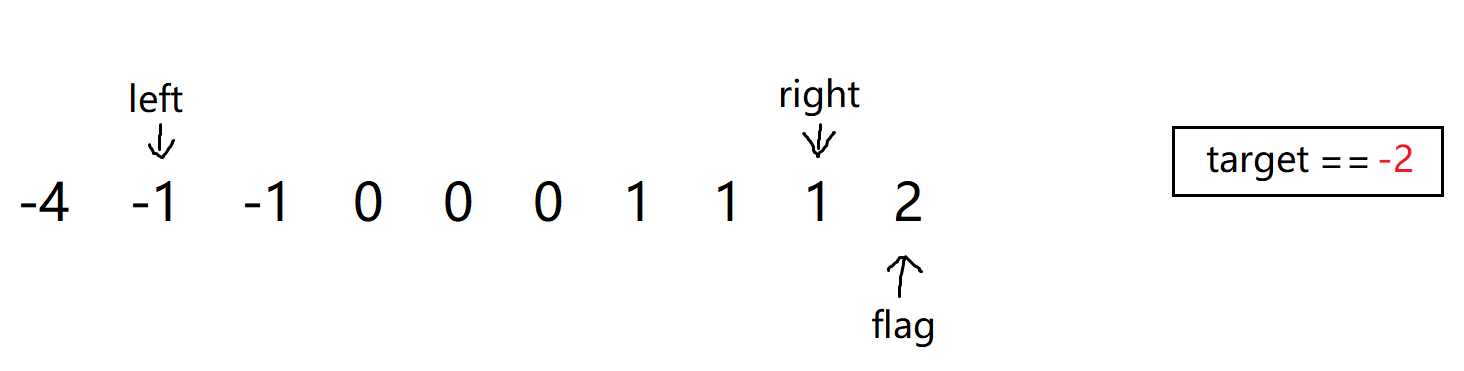
接下来又发现nums[left] + nums[right] > target（-1 + 1 > -2），所以我们需要将right--：
后面我们就不断进行操作，直到遇到这种情况：
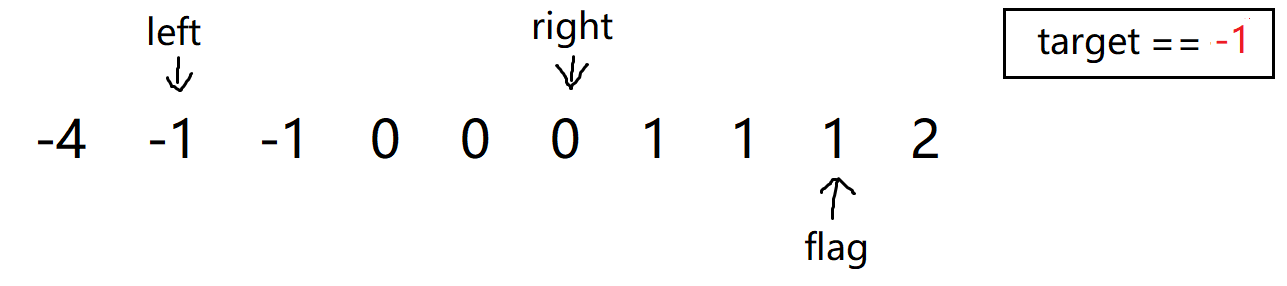
这个时候就非常完美，因为此时的nums[left] + nums[right] == target（-1 + 0 == -1），所以我们直接push_back就好了，但是接下来该怎么办呢？如果直接break掉，对于这个例子是可以的，但是万一这之中也有满足的条件呢？因此这种情况是不能break掉的，我们还需要继续判断，所以我们直接++left和--right，但是对于他们俩，在进行left++和right--之后，会发现还是为-1和0：
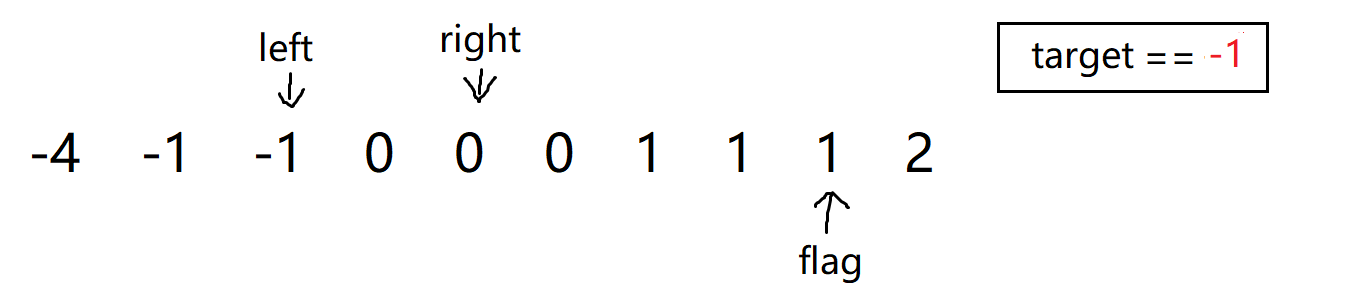
- 所以我们其实可以直接跳过这些，因为再进行一次判断也是浪费时间，所以直接用 while循环来处理就好，但是这里一定要注意喔，你可不要对 right 一直不断遍历判断然后就把right搞越界了，所以我们还需要先进行越界问题的处理：
  while(left < flag && nums[left] == nums[left - 1]) ++left
  while(right >=0 && nums[right] == nums[right + 1] --right)
- 最后处理完之后 right 就会在 left 的左侧了，所以当前的这一趟循环就结束了，然后就会flag--进入下一趟：
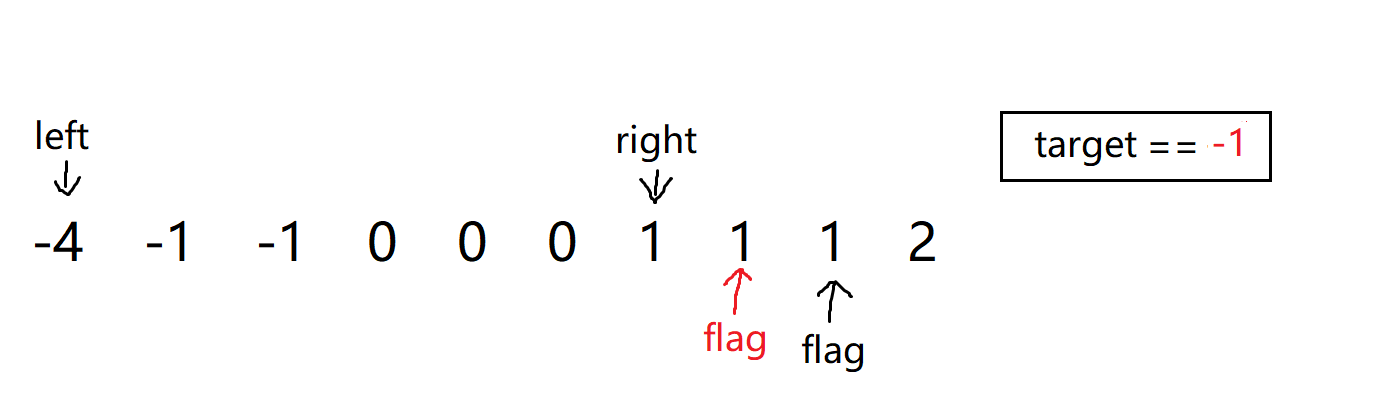
- 可是这个flag还是和之前一样啊，那你判断的话岂不是又要再进行一次判断了？那你百分之百又会遇到那几个数字，那你在存放答案的容器vector中不就出现重复的答案了嘛，所以这肯定是不对的，我们最关键的就是在这里进行判断，然后实现去重，去重的操作和上述一样，然后就是一定要避免越界：
  
  while(flag > 1 && nums[flag] == nums[flag + 1]) --flag
- 其实到这里就差不多了，但是我们再仔细观察观察就会发现，好像flag变成负数之后，就绝对不可能有匹配的数字了，因此我们还可以对flag进行“剪枝”操作，作为第一个while循环标志你有走多少趟：
  while(flag > 1 && nums[flag] >= 0))

✅《四数之和》

🌹题目描述：

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

🚗代码实现：

class Solution 
{
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(), nums.end());vector<vector<int>> vv;int index = nums.size() - 1;while(index > 2){int flag = index - 1;while(flag > 1){int left = 0, right = flag - 1;while(left < right){if(nums[left] + nums[right] > (long)target - nums[flag] - nums[index]) --right;else if(nums[left] + nums[right] < (long)target - nums[flag] - nums[index]) ++left;else{vv.push_back({nums[left], nums[right], nums[flag], nums[index]});++left, --right;while(left < right && nums[left] == nums[left - 1]) ++left;while(right > left && nums[right] == nums[right + 1])--right;}}--flag;while(flag > 1 && nums[flag] == nums[flag + 1]) --flag;}--index;while(index > 2 && nums[index] == nums[index + 1]) --index;}return vv;}
};

😴代码解析：

本道题的代码说实话就是基本照搬上面讲解的《三数之和》的代码，如果你能理解上面所讲解的《三数之和》那你一定也能理解这里的《四数之和》！

步骤一开始都是一样的，先进行排序，然后再通过双指针算法来遍历数组。这道题无疑就是多了一个数呗，那又何妨呢？思路还是一样的，只是多了一个while循环罢了。如果你理解了上述的《三数之和》，那么这道题对你来说不成问题，在这里我就不过多赘述。

值得注意的是，在处理target - nums[flag] - nums[index]时，可能会出现下列情况，这是因为出现了整形溢出的问题

nums = [1000000000,1000000000,1000000000,1000000000]

target = -29496729

Line 17: Char 71: runtime error: signed integer overflow: -1294967296 - 1000000000 cannot be represented in type 'int' (solution.cpp) SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior solution.cpp:17:71

我们只需要对target - nums[flag] - nums[index]进行强制类型转换即可:(long) target - nums[flag] - nums[index.