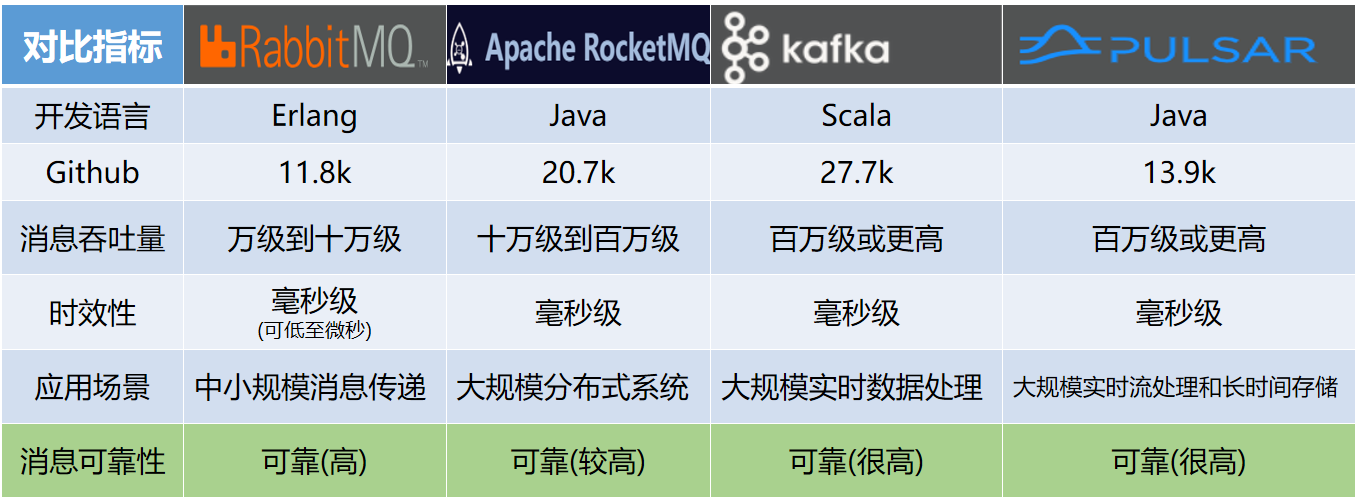
本文将详细介绍IQ Tool中的Radar Pulses/Chirps模块的使用方法和实现原理。

1. 参数配置

图1. Radar Pulses/Chirps参数配置界面

  该模块可配参数如下：
  (1) Sample Rate(Hz): 系统采样率，单位:Hz
  (2) Repeat interval(s): 脉冲重复周期，单位:s
  (3) Pulse width(s): 脉冲宽度，单位:s
  (4) Rise time(s): 上升时间，单位:s
  (5) Fall time(s): 下降时间，单位:s
  (6) Initial Delay(s): 初始时延，单位:s
  (7) Pulse Shape: 脉冲形状，目前包括4种选项，Raise Consine、Trapezodial、Gaussian和Zero signal during rise time。
  (8) Modulation on Pulse： 不同相位调制形式， 目前支持19种形式，后面会进行详细说明。
  (9) Freq.mod.formula: 频率调制形式，目前发现只有在Modulation on Pulse设置为user defined时，才能使能。暂时还没弄清楚具体是怎样作用的。
  (10) Phase mod.formula: 相位调制形式，该参数只有在Modulation on Pulse选择“Custom IQ”时生效，用户输入一个数学表达式表示脉冲信号的相位调制。
  (11) Amplitude(dB)： 信号幅度，单位：dB
  (12) Frequency span: 该参数仅在Modulation on Pulse参数选择"Increasing"、“Decreasing”、“V-shape”、“Inverse-V”、“FMCW”、“Frank-4”、"Frank-6"和"User Defined"的时候能够使能，用于表征脉宽内信号的频率跨度，对频率值做积分即可得到相位值。该参数本质上是用于计算波形的相位特性。
  (13) Frequency offset: 与Frequency span配合使用，确定具体的频率范围。
  (14) Apply Correction: 是否使用预失真的方式来补偿AWG的幅相不平衡
  (15) Download: 用于选择将I/Q信号下载到哪个通道中。
  (17) Segment Number: 不清楚这个分段数指的是什么·
  (18) Fc(VSA setups): 不清楚是什么含义
  除了上面的配置参数意外，在这个界面的菜单栏中还有一些配置，如在File选项卡中，可以选择将当前配置保存成配置文件、导入已有配置文件、保存生成的波形、将当前配置生成matlab等。在Preset选项卡中，有一些常用的配置可供直接选择，便利用户的使用过程。在界面的下面，还有一些图形显示、下载等功能按钮。
  【备注】
  (1) 该功能模块可以跳过上述参数配置界面，直接调用文件iqpulse.m在命令行中生成需要的波形。举例如下：

iqpulse('sampleRate', sampleRate)

  (2) 直接在命令行调用iqtone()这个函数时，若没有给定输入参数，则会自动弹出上述参数设置框；若给定了输入参数则按给定的输入参数进行波形生成。
  (3) Repeat interval(s)、Pulse width(s)、Rise time(s)等等这些参数均是与每个脉冲对应的，即理论上要生成$N$个脉冲信号，上述各参数维数就为$N$，但是在参数输入的时候有可能没有保持上述各个采纳数的维数一致，则程序会自动以最长的那个参数的维数作为生成的脉冲数。

2. 波形生成原理

  参数配置完成后，即进入波形生成环节，包含以下步骤：

2.1 参数配置

  调整配置参数，保证各个参数的合理性，这里面的操作包括：a) 调整脉冲信号的各项参数，如幅度、上升/下降时间、脉宽等，使得这些参数的维度保持一致；b）通过调整PRI，使得最终的采样点数为AWG Granularity的整数倍(具体如何调整见《》)。

2.2 生成脉冲波形的幅度包络

  生成脉冲波形的幅度包络。下图为生成的脉冲示意图，其中$dela{y}_i$、$r{t}_i$、$f{t}_i$、$p{w}_i$、$p{r}_i$分别表示第$i$个脉冲波形的延时(delay)、上升时间(rise time)、下降时间(fall time)、脉冲宽度(pulse width)和脉冲重复周期(pulse repeated interval)。完整波形由每个脉冲波形拼接而成，而每个脉冲波形的生成过程都一样，故这边以一个脉冲波形的生成为例说明具体过程：
  (1) 设一个脉冲波形序列为$s[n]$，其默认为全零序列。首先求下图所示$t_1-t_4$这4个关键时间点，并计算各个时间点对应的索引分别为$I_1$、$I_2$、$I_3$、$I_4$。这四个时间点将一个脉冲波形分成5段，只需分别往这5段里面填入对应的序列即可。
  (2) 显然， 波形中平稳阶段的值很好给定，具体地(matlab中数据索引由1开始)$s[1:I_1]=0$, $s[N-I_4:end]=0$、$s[I_2+1:I_3]=A$。波形中的上升、下降阶段根据Pulse Shape参数的不同进行设置，如Pulse Shape=raise cosine，则上升沿设置为raise cosine左半边波形(如图3所示，$\beta$设为1)，下降沿设置为raise cosine右半边波形；Pulse Shpae=trapezodial，则上升沿设置为正斜率的直线形状(图2所示)，下降沿设置为负斜率的直线形状；若Pulse Shape=gaussian，则上升沿设置为gausswin左半边波形(如图4所示，$\alpha$设为5)，下降沿设置为gausswin右半边波形；若Pulse Shape=zero signal during rise time，则上升和下降时段的值全部设置为0。

图2. 生成的波形示意图

2.3 生成脉冲波形的相位

  (1) 若Modulation on Pulse设置为"Increasing"、“Decreasing”、“V-shape”、“Inverse-V”、"FMCW"时，计算步骤如下：
   a) 下图为上述几种配置对应的频率调制趋势图，设该趋势为fm_on(该变量名和程序中的变量名保持一致)

图3. 频率调制下的相位值

   b) 将上面的调制趋势转化为具体的频率调制，具体地：

fmTmp=(span/2 *fm_on) + offset

  上式中各个变量的命名与程序中各变量的命名保持一致。span表示频率跨度(通过界面中“Frequency span”设置)，offset表示频率偏移(通过界面中"Frequency offset"设置)。举例说明，若Modulation on Pulse=“Increasing”, span=100MHz， offset=0Hz，则fmTmp表示-50MHz~50MHz线性递增的频率。【注】：fmTmp表示单位为"Hz"的瞬时频率。

   c) 将上述瞬时频率频率调制转化为瞬时相位，瞬时相位是瞬时频率的积分，具体地

pmTmp=cumsum(fmTmp) / sampleRate

  上式中各个变量的命名与程序中各变量的命名保持一致。sampleRate表示采样率，上面得到的pmTmp是单位为$rad/(2\pi )$。

   d) 将初始相移phaseOffset(通过界面Initial Phase设置)、初始时延timeOffset(通过界面Initial Delay设置)造成的相移也考虑进去，得到最终的相位序列。

  (2) 若Modulation on Pulse设置为"Barker-2 + -", “Barker-2 ++”, “Barker-3 ++ -”, “Barker-4 ++ - +”, “Barker-4 +++ -”, “Barker-5”, “Barker-7”, “Barker-11”, "Barker-13"时，相位生成的逻辑很简单，举例说明：若Modulation on Pulse=Barker-2 + -，则前半个脉冲重复周期(PRI)的相位为90°，后半个脉冲重复周期(PRI)的相位为-90°。若Modulation on Pulse=Barker-3 ++ -，则前2/3个脉冲重复周期(PRI)的相位为90°，后1/3个脉冲重复周期(PRI)的相位为-90°，以此类推至其他的Barker调制模式。所有Barker调制生成的相位如下图所示

图4. 不同Barker调制模式的相位值

  (3) 若Modulation on Pulse设置为"Frank-4", "Frank-6"时，按附录4.4生成对应的相位序列，如下图所示

图5. 不同Frank调制模式的相位值

  (4) 除了上述各种可选相位外，程序还支持用户通过表达式自定义各种相位情况，这边不进行过多赘述。

2.4 组合成完整信号

  通过2.2生成脉冲包络$A(t)$和2.3生成脉冲相位$\theta (t)$后，即可组合成完整信号
$$s(t)=A(t)exp(j\theta (t))$$
  下面给出生成的几种波形示意图

图6. 不同Barker调制模式生成的相位示意图

图7. 不同Frank调制模式生成的相位示意图

2.5 对信号进行后处理

  生成上述波形后，可选择对波形进行一些后处理，包括幅度归一化、预失真、通道映射等。所有这些操作均与其他波形生成模块是一致的，故不再这边细说，后面将进行专题说明。

---

4. 附录

4.1 升余弦函数

  升余弦滤波器(Raise-cosine filter)经常被用作脉冲成型滤波器，它能够最大限度地减小码间干扰(ISI)。之所以会如此命名是因为，该滤波器的最简形式频谱($\beta =1$)的非零部分为余弦函数被抬升至x轴上方。其表达式为一个分段函数，不同$\beta$情况下的升余弦函数图像如下图所示。
$$H(f)=\{\begin{array}{l}1,|f|\le \frac{1-\beta }{2T_s}\\ \frac{1}{2}[1+cos(\frac{\pi T_s}{\beta }[|f|-\frac{1-\beta }{2T_s}])],\frac{1-\beta }{2T_s}<|f|<\frac{1+\beta }{2T_s}\\ 0,otherwise\end{array}$$

图8. 不同beta值的升余弦函数示意图

4.2 高斯窗函数

  高斯窗函数的表达式为
$$w[n]=exp(-\frac{1}{2}(\alpha \frac{n}{(L-1)/2}{)}^2)=exp(-n^2/2{\sigma }^2)$$
  在上面的表达式中，$-(L-1)/2\le n\le (L-1)/2$，$\sigma =(L-1)/2\alpha$，$\sigma$表示高斯分布的标准差。显然$\alpha$越大，$\sigma$越小。下图为不同$\alpha$值对应的高斯窗。

图9. 不同alpha值的高斯窗函数

4.3 Barker Code

  雷达探测要求既要探得远，也要探得准。要想探得远要求雷达的平均功率要高，所以在脉冲重复周期内，脉冲宽度要尽可能大。要想探得准，要求雷达的距离分辨率高，此时又要减小脉冲宽度。所以雷达探测距离和距离精度是一对互相矛盾的参数。雷达距离分辨率为$c/2B$，对于简单脉冲信号来说，其时宽带宽积为1(即信号频谱带宽和脉冲宽度乘积为1)，所以提高脉冲宽度势必导致频谱带宽降低。为了解决雷达探测距离和距离精度的矛盾，要求提高信号的时宽带宽积，通常可通过对特定脉宽的脉冲信号进行频率(常见的频率调制如线性调频)或相位调制来提高信号带宽，从而提高时宽带宽积。此外，为了减少模糊目标(虚假目标)，要求雷达信号的模糊函数呈现图钉形状，即信号要具有良好的自相关特性。Barker Code(巴克码)是雷达中一种常用的相位调制编码。

图10. 不同脉冲信号对比

  巴克码是一种二相编码，二相编码的基本做法可以用上图中中间图形进行说明，它将一个宽脉冲信号分成多个窄单元，每个单元被“+”(代表﹢1)或"-"(代表-1)进行编码，正号表示正常的载波相位，符号表示进行180°相移。巴克码自相关函数的主/幅瓣比等于压缩比，即等于码长$N$，幅瓣均匀，是一种比较理想的编码脉冲压缩信号。可惜它的长度有限。已经证明，对于奇数长度，$N\le 13$；对于偶数长度，$N$为一完全平方数，但已证明$N$在4和6084之间不存在，超过6084的码一般不采用。巴克码的自相关函数为
$$\Phi (m)=\{\begin{array}{l}N,m=0\\ 0或1,m\ne 0\end{array}$$
  目前常用的巴克码如下表所示

码组长度	Barker 码组	自相关函数	主旁瓣比(dB)
2	++, + -	2,1;2,-1	6
3	++ -	3,0,-1	9.6
4	+++ -, ++ - +	4,-1,0,1;4,1,0,-1	12
5	+++ - +	5,0,1,0,1	14
7	+++ - - + -	7,0,-1,0,-1,0,-1	17
11	+++ - - - + - - + -	11,0,-1,0,-1,0,-1,0,-1,0,-1	20.8
13	+++++ - - ++ - + - +	13,0,1,0,1,0,1,0,1,0,1,0,1	22.2

4.4 Frank Code

   Frank编码和巴克码一样都是相位编码，只不过巴克码是二相编码(只在两个固定相位之间跳转)，Frank是多相编码(可在多个相位之间跳转)。Frank码的长度是某些正整数$M$值的平方，即码长$N=M^2$，相位序列为
$$\varphi (n)=\varphi (Mp+q)=\frac{2\pi }{M}pq,p=0,1,...,M-1,q=0,1,...,M-1$$
   例如，如果M=4，则$N=16$，相位序列为
$$\varphi =[0,0,0,0,0,\frac{\pi }{2},\pi ,\frac{3\pi }{2},0,\pi ,0,\pi ,0,\frac{3\pi }{2},\pi ,\frac{\pi }{2}]$$
   一般地，Frank码的相位序列也可以写成一个$M\times M$的矩阵，即
$$\frac{2\pi }{M}\times \left[\begin{array}{ccccc}0& 0& 0& ...& 0\\ 0& 1& 2& ...& M-1\\ 0& 2& 4& ...& 2(M-1)\\ ⋮& ⋮& ⋮& ...& ⋮\\ 0& M-1& 2(M-1)& ...& (M-1{)}^2\end{array}\right]$$