目录

1、文件功能介绍

2、代码执行效果展示

3、Dijkstra算法求图的单源最短路径

4、Dijkstra fullPath的更新逻辑

5、DIjkstra算法流程图

6、Floyd算法实现图的任意两点间最短路径

7、Floyd算法流程图

8、Floyd fullPath的更新逻辑（非递归算法）

---

1、文件功能介绍

代码文件	功能
workspace.m	代码一步执行工作区
Dijkstra.m	Dijkstra算法计算最短路径的距离dist和路径fullPath以及置定节点集Gp
Floyd.m	Floyd算法获得完全优化后的权值矩阵W和路由矩阵R
getGraph.m	获取网络图（默认图或者手动输入）
getFloydMinPath	利用Floyd计算得到的W和R获取任意起点v到其他节点的最短路径fullPath及距离dist
drawPath	利用fullPath、dist、point（随机值获取）、figureIndex(图的句柄)，绘制对应的最短路径
drawDijkstraPath.m	绘制Dijkstra各轮下对应的最短路径

---

2、代码执行效果展示

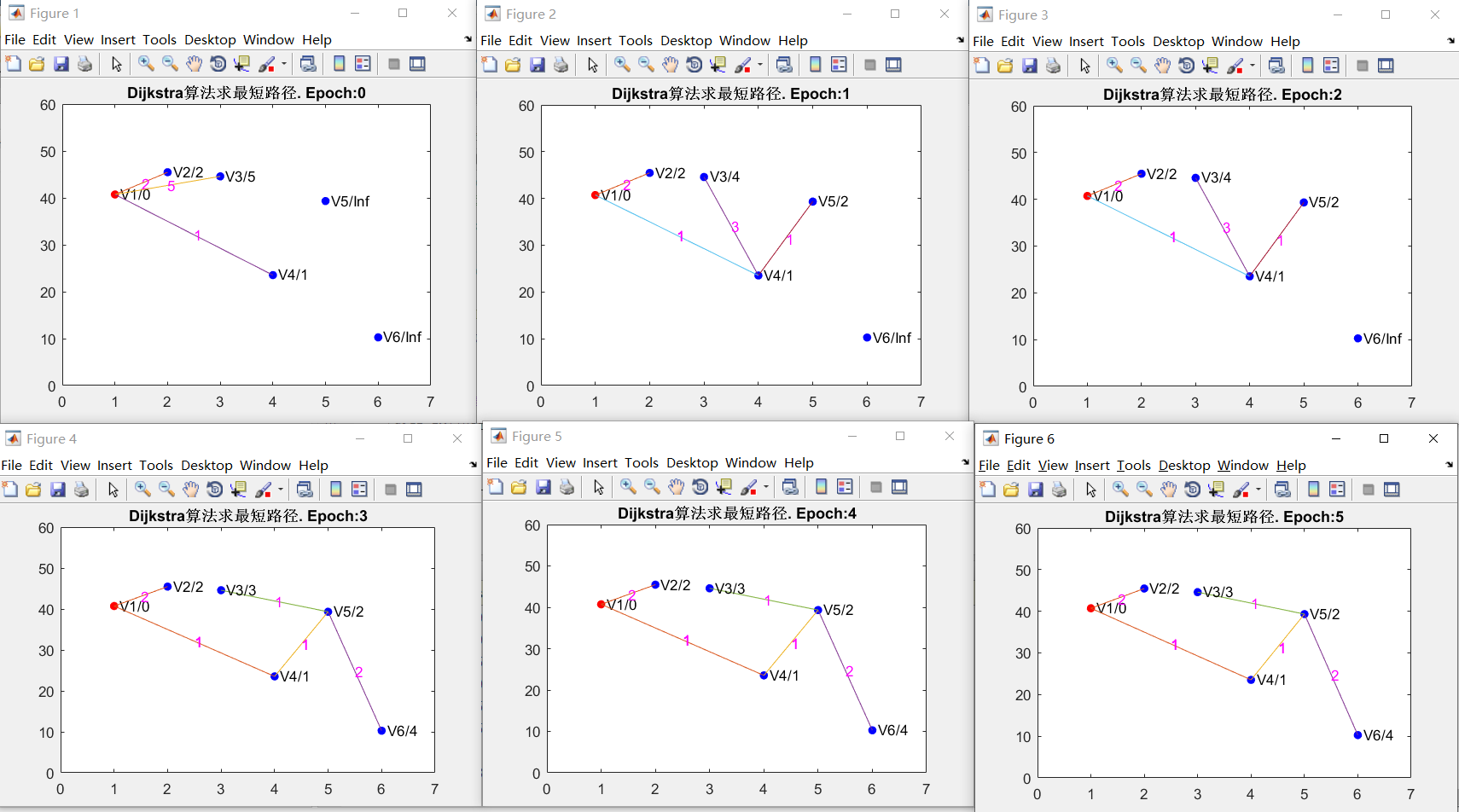
Dijkstra执行效果图，可看到每一轮更新之后的最短路径情况。

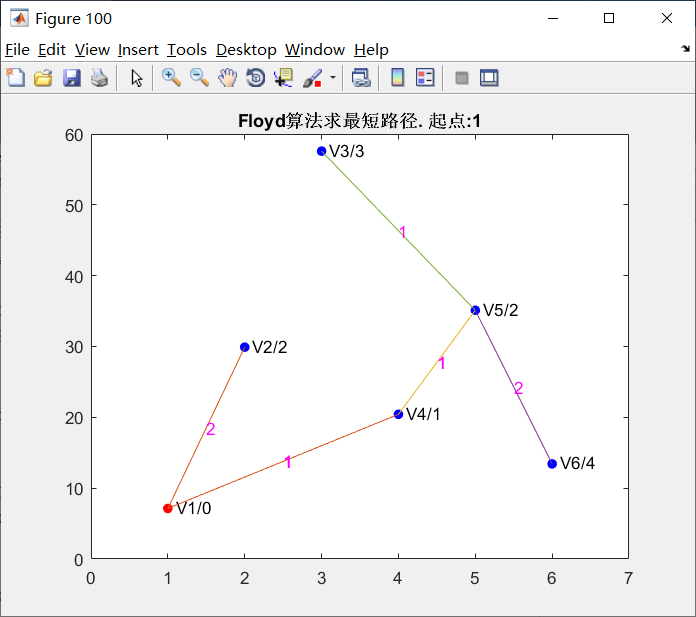
​Floyd执行效果图，可看到执行起点v到其他各节点的最短路径。

3、Dijkstra算法求图的单源最短路径

算法思想简述如下： 将图中各点分为两个集合：置定结点集合Gp（并入了最短路径的）、非置定结点集合Gs. 使用dist记录源点v到各点的距离，fullPath记录源点v到其余各点的最短路径.

• 将源点v加入置定结点集合Gp

• 找出置定结点集合Gp到Gs的当前最短边（及其对应顶点k）

• 将该顶点k加入到置定结点集合Gp中，利用k作为中间结点，如果Gp中(i->k+k->j)<(i->j)，则更新Gp到Gs的路径，并将中间结点k记录到对应dist中

• 循环运行n-1次，将所有剩余结点加入到Gp中

4、Dijkstra fullPath的更新逻辑

• fullPath记录的是源点v到各顶点的最短路径（起点->中间结点s->终点）

• 当新的顶点k加入到Gp后，需要利用k作为中间结点更新Gp到Gs的路径，若此时有结点i,j(i属于Gp,j属于Gs)，满足(i->k+k->j)<(i->j)，则认定源点到j点需要经过中间结点k

• 将k结点的当前fullPath对应最短路径，赋值给j的fullPath对应最短路径（记录下来到中间结点k的前面的路径）。

• 在j的最短路径后面加上当前的结点号j（终点记录）。

5、DIjkstra算法流程图

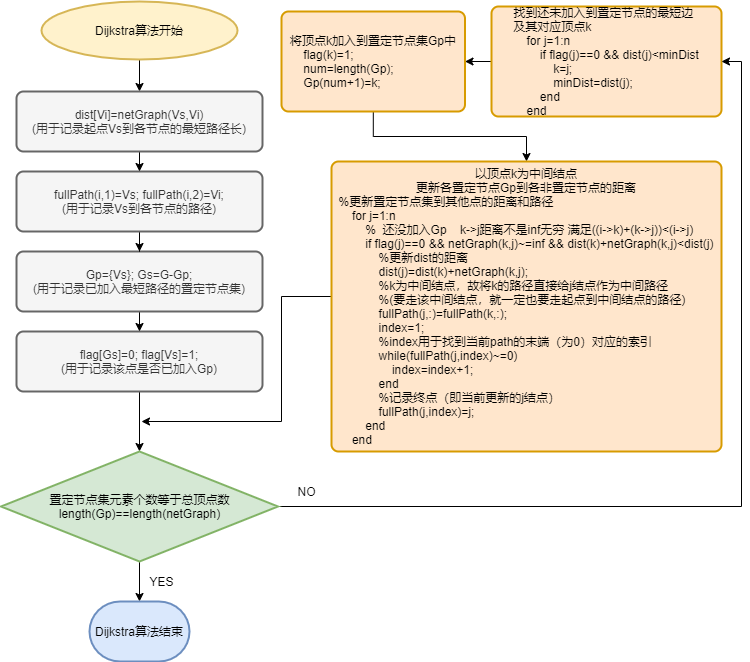
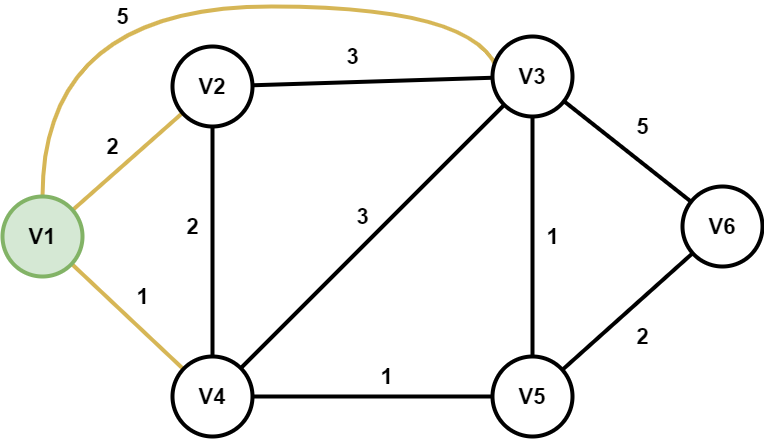
初始化Dijkstra图，标出起点V1（置定节点集Gp此时只有V1），及置定节点集Gp与非置定节点集的连线（橙色线. V1-V2,V1-V3,V1-V4）。

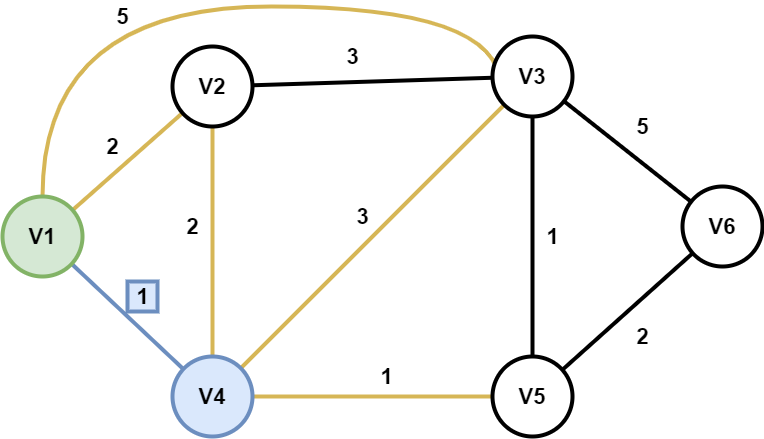
选取置定节点集Gp与非置定节点集的连线（橙色线）中最短的那条线（V1-V4），将V4并入置定节点集（节点V4及其连线V1-V4标蓝），同时更新置定节点集Gp与非置定节点集的连线（橙色线. V4-V2,V4-V3,V4-V5）。

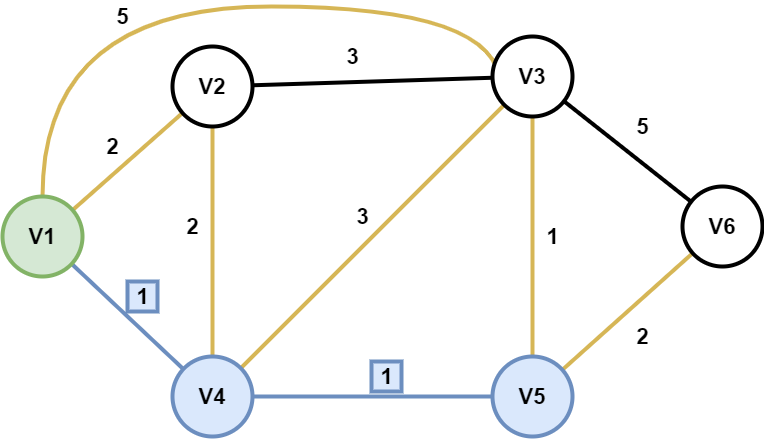
选取最短的那条线（V4-V5），将V5并入置定节点集（节点V5及其连线V4-V5标蓝），同时更新置定节点集Gp与非置定节点集的连线（橙色线.V5-V3,V5-V6）。

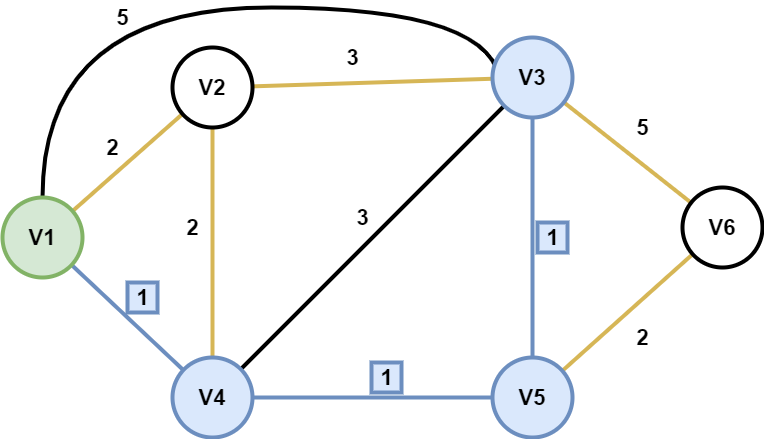
选取最短的那条线（V5-V3），将V3并入置定节点集（节点V3及其连线V5-V3标蓝），同时更新置定节点集Gp与非置定节点集的连线（橙色线.V3-V2,V3-V6），移除置定节点集本身间的连线（V1-V3.V4-V3）。

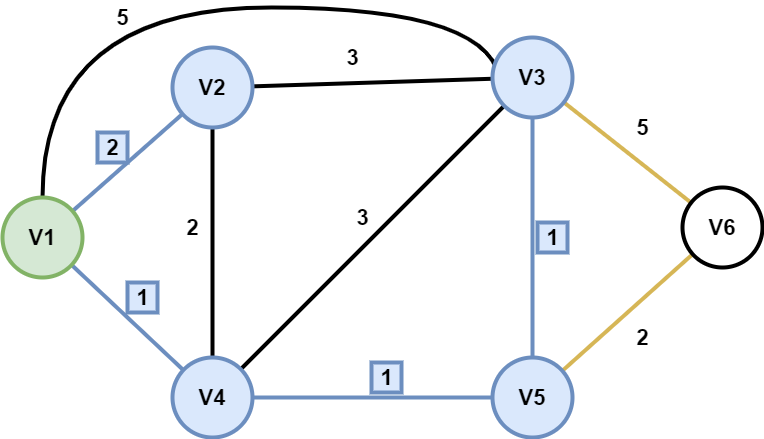
选取最短的那条线（V1-V2），将V2并入置定节点集（节点V2及其连线V1-V2标蓝）。

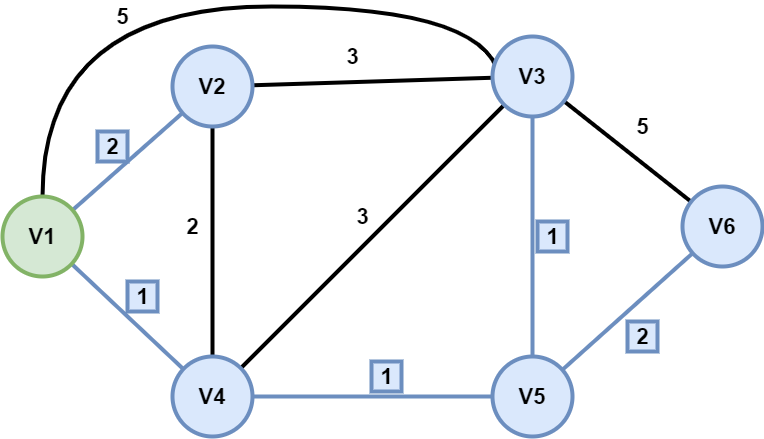
选取最短的那条线（V5-V6），将V6并入置定节点集（节点V6及其连线V5-V6标蓝），此时置定节点集包含所有节点，Dijkstra构造完成最短路径。

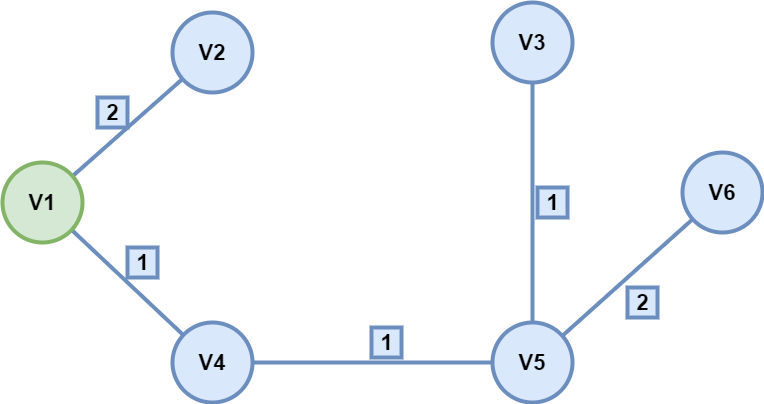
6、Floyd算法实现图的任意两点间最短路径

算法思想简述如下： 如果要让任意两点（例如从顶点a点到顶点b）之间的路程变短，只能引入第三个点（顶点k），并通过这个顶点k中转，即a->k->b，才可能缩短原来从顶点a点到顶点b的路程。 图的权值矩阵W(Weight，记录一点到任意各点的最短距离)、最短路由矩阵R(Router，记录中间结点路由) 首先以第一个顶点(k=1:n)作为第一个中间结点， 遍历权值矩阵(i=1:n,j=1:n)来寻找是否能利用当前结点k=1为中间结点，使得w(i->k+k->j)<w(i->j)，若满足，则更新(i->j)的距离W(i,j)=w(i->k+k->j)，同时更新中间结点路由R(i,j)=k； 利用k=1:n所有结点作为中间结点进行W和R的优化后，最终得到的W和R即为最短路径W和最短路径路由矩阵R.

7、Floyd算法流程图

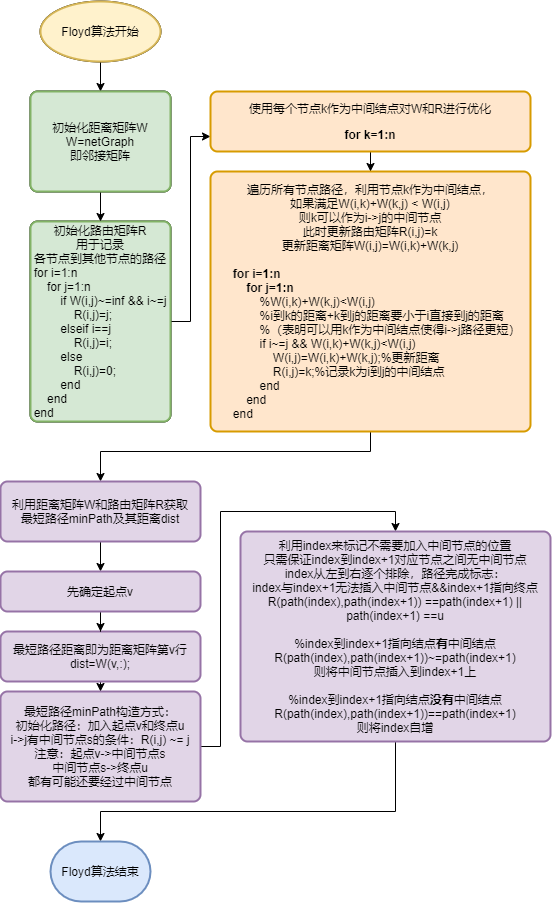
8、Floyd fullPath的更新逻辑（非递归算法）

• 由于Floyd算法的关键就是利用中间结点优化源点v到终点u的路径

• 当找到一个可优化的中间结点k时，将k插入到源点v和终点u中间(v->k(中间结点)->u)

• 这时候，需要注意到，v->k可能有中间结点可以优化，k->u也可能有中间结点可以优化，我们需要做这两件事情：1.不断找中间结点插入到路径；2.保证各段没有中间结点可以再优化了

• 怎样保证能把所有中间结点都记录下来呢？没有中间结点可优化的条件(R(path(index),path(index+1))==path(index+1))

• 设立一个index记录之前已经完成了最优化，一个rNum记录中间结点的个数（便于插入新中间结点），不断寻找index到index+1顶点的中间结点并插入到index到index+1顶点中间，知道index到index+1之间没有中间结点(R(index,index+1)==index+1)，这时候令index加一，去更新下一级的index到index+1的中间结点，由此不断优化，不断向前推index，最终当所有的路径都已经没有中间结点可以增加时path(index+1)==u，则表示最优化达到了终点，完成了路径检索。

项目资源下载：https://download.csdn.net/download/m0_38106923/87740211