从0开始的算法（数据结构和算法）基础（十一）

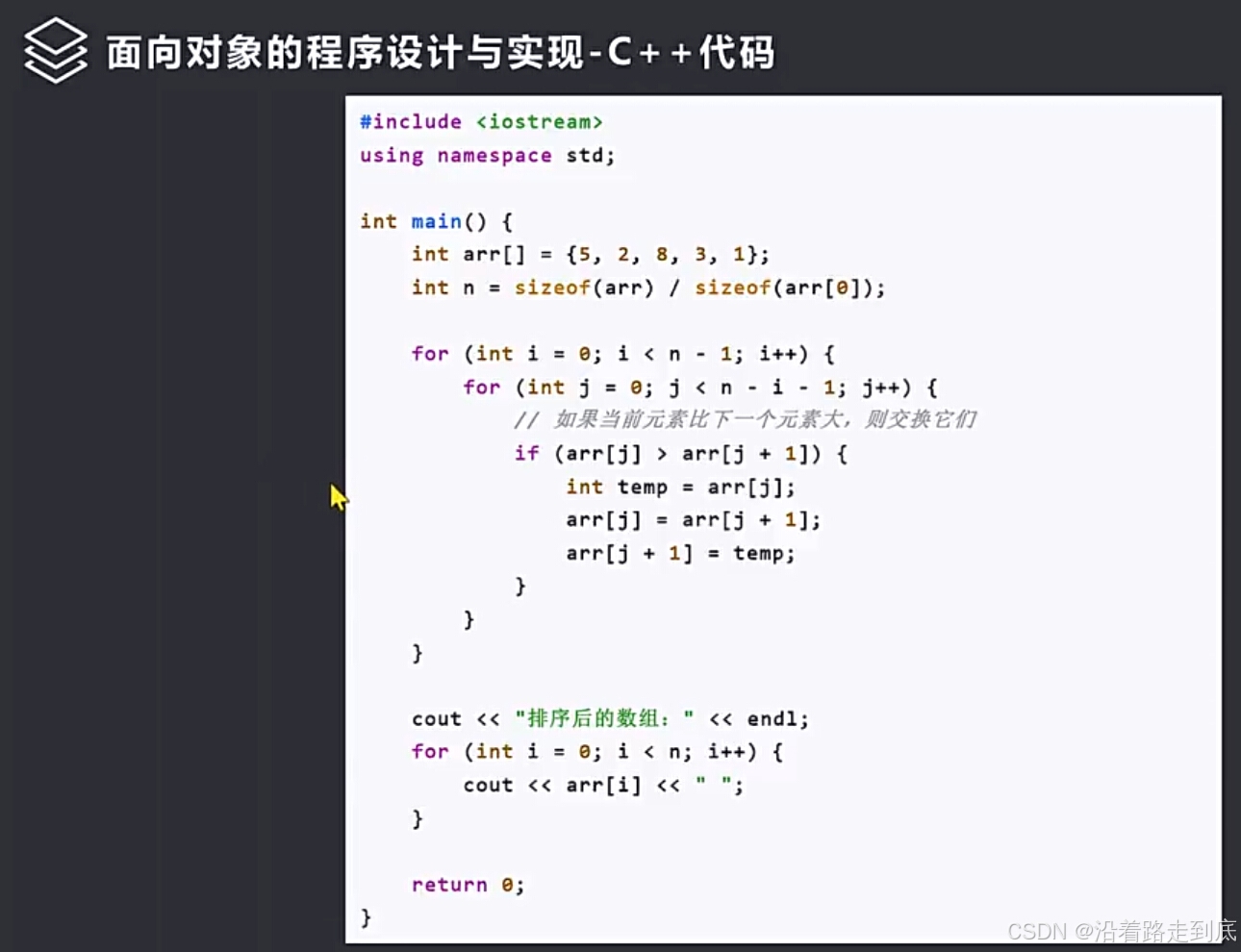
回溯算法

什么是回溯算法

回溯算法，根据字面意思来理解这个算法是将每一步的操作可以进行回溯，实际上是对这个每一步的操作进行记录，确保可以返回上一步的操作，可能是对回溯操作之前的做一个复现，也有可能是可操作的回退，这个观点是错误的，通过尝试不同的选择并记录当前状态，当遇到不符合要求的解时，能够回溯到之前的状态进行新的尝试，备份回退。 特别适用于解决组合、排列、子集等问题。其核心思想是在搜索过程中，我也不知道为什么，因为在我的理解里面觉得，只要能够回到当前的状态，重新做一个复现，也是可以的只不过耗费时间和空间，一个更大型的穷举，而且可以确定问题出现的多个地方的可能性。

leetcode经典问题

为了解释回溯算法的实际应用流程，我将提供一个简单的回溯算法流程图，以及一个使用 Java 实现的回溯算法示例。以下是解决N 皇后问题的回溯算法流程图及其 Java 代码。

回溯算法流程图

流程图说明

开始: 算法启动。
初始化变量: 设置棋盘大小和用于存放皇后位置的数组。
调用递归函数: 从第一行开始尝试放置皇后。
是否所有皇后都已放置?: 检查当前行是否已放置所有皇后。
- 是: 记录当前解，并结束算法。
- 否: 继续尝试在当前行放置皇后。
在当前行的每一列尝试放置皇后: 遍历当前行的所有列。
放置是否合法?: 检查当前放置的皇后是否冲突。
- 是: 继续递归到下一行。
- 否: 尝试在当前行的下一个列放置皇后。

您可以将上述 Mermaid 代码粘贴到支持 Mermaid 的工具或编辑器中（如 Markdown 编辑器、Mermaid Live Editor 等），来查看生成的流程图。希望这能帮助您理解回溯算法的流程！

Java 实现代码：N 皇后问题

以下是一个回溯算法在 Java 中解决 N 皇后问题的示例：

import java.util.ArrayList;
import java.util.List;public class NQueens {public static void main(String[] args) {int n = 4; // 可以改变n的值，来测试不同的棋盘大小List<List<String>> solutions = solveNQueens(n);for (List<String> solution : solutions) {for (String row : solution) {System.out.println(row);}System.out.println();}}public static List<List<String>> solveNQueens(int n) {List<List<String>> result = new ArrayList<>();int[] queens = new int[n];solve(0, n, queens, result);return result;}private static void solve(int row, int n, int[] queens, List<List<String>> result) {if (row == n) {result.add(generateBoard(queens, n));return;}for (int col = 0; col < n; col++) {if (isValid(queens, row, col)) {queens[row] = col;solve(row + 1, n, queens, result);queens[row] = -1;  // 回溯}}}private static boolean isValid(int[] queens, int row, int col) {for (int i = 0; i < row; i++) {if (queens[i] == col || Math.abs(queens[i] - col) == Math.abs(i - row)) {return false;}}return true;}private static List<String> generateBoard(int[] queens, int n) {List<String> board = new ArrayList<>();for (int i = 0; i < n; i++) {char[] row = new char[n];for (int j = 0; j < n; j++) {row[j] = (queens[i] == j) ? 'Q' : '.';}board.add(new String(row));}return board;}
}

代码解读

solveNQueens 方法：初始化棋盘，并调用 solve 方法开始递归。
solve 方法：这个方法使用递归来尝试在每一行放置皇后，并检查当前位置是否安全。如果皇后可以安全放置，则继续递归地解决下一行的问题；如果没有合法的位置，则回溯到前一个状态。
isValid 方法：检查当前放置皇后的状态是否合法，即是否与前面已经放置的皇后发生冲突。
generateBoard 方法：当找到一个解时，生成该解对应的棋盘表示，并将其加入到结果集中。

回溯算法实际应用场景

回溯算法被广泛应用于以下场景：

组合问题：比如组合、排列、子集问题。
图问题：如迷宫问题、图着色问题。
搜索问题：如数独、八皇后问题等。
排列和优化问题：如旅行商问题、背包问题等。

实际生活中的应用

回溯算法在解决组合、排列、约束满足问题等复杂问题时非常有效，它不仅用于计算机科学和数学中，还在实际生活中有广泛的应用。以下是一些回溯算法在实际生活中的应用场景：

1. 旅行路线规划

应用场景：旅行者需要规划一条从起点到终点经过多个城市的路线，并且可能有时间、距离等限制。
回溯算法的作用：回溯算法可以尝试不同的路线组合，评估每一条路线是否满足约束条件（如最短距离或最低花费）。如果某条路线不符合要求，则回退并重新尝试其他路线，最终找到最优解。

滴滴司机顺风车的固定路线的产生
在这里插入图片描述

2. 课程安排与考试安排

应用场景：学校或大学的课程安排或考试安排，必须考虑到多个约束条件（如教师的时间、教室的数量、学生的选课冲突等）。
回溯算法的作用：回溯算法通过尝试不同的安排方式，逐步构建课程或考试安排表，并在发现安排冲突时，回溯到前一步重新安排。它可以帮助生成一份符合所有约束条件的合理排课表或考试表。
在这里插入图片描述