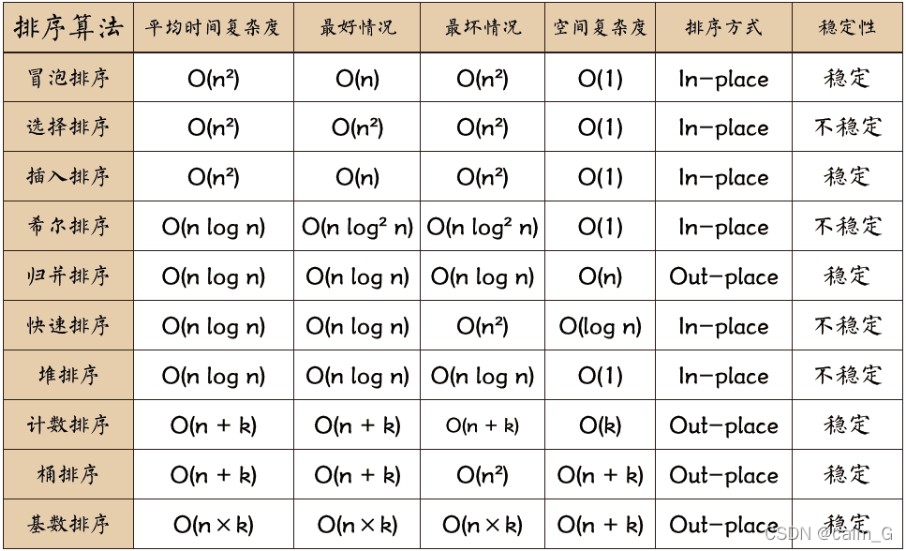
支持向量机(线性) $SVM$

引入

  $SVM$ 用于解决的问题也是 $classification$，这里 y ∈ { − 1 , 1 } y \in \{-1, 1\} y∈{−1,1}

  比如说这样一个需要分类的训练数据：

  我们可以有很多直线来分开这两坨东西，就像这样：

  我们看到这三条线 $l_1,l_2$ 和 $l_3$，我们显然可以看出来 $l_1$ 比 $l_2$ 和 $l_3$ 要更优秀，但是我们怎么定义这个所谓的 “优秀” 呢？

间隔 $Margin$ 和 最小化 $|w|$

  我们这样理解，考虑将 $l$ 在样本空间中平移，直到这条直线第一次碰到两组东西数据时停止。这样我们能得到两根 “边界线”（图中绿色的线）。

  我们发现，我们认为最优秀的线所形成的 “边界线” 的距离是最大的，我们把这个距离成为间隔 $margin$。于是在 $SVM$ 的思想中，我们就是要找到 $margin$ 最大的那条线。

  我们把这些"平移过程中第一次碰到的向量"称为支持向量

  我们把这条线根据之前的习惯写成这样：

$$h(x)=w^{T}x$$

  然后我们考虑如何计算出 $margin$。首先对于一个支持向量 $x^{(i)}$ 来说，它到直线的距离可以写成：

$$d=\frac{\left|\sum _{j=0}^n{w}_j{x}_j^{(i)}\right|}{\sqrt{\sum _{j=1}^n{w}_j^2}}=\frac{\left|w^T{x}^{(i)}\right|}{|w|}$$

  然后又因为我们知道，$h(x)=w^{T}x$ 和 $h(x)=(aw{)}^{T}x$ 本质上表示的是同一条直线（其中 $a$ 是常数）。所以我们可以用 $a$ 来放缩直线 $h(x)$，使得 $|(aw{)}^T{x}^{(i)}|=1$。

  此时，支持向量 $x^{(i)}$ 到直线的距离就是：

$$d=\frac{1}{|w|}$$

  我们希望 $d$ 最大，那么我们就希望 $|w|$ 最小了。

  但是这只是对于支持向量来说，那么对于其他向量来说又要满足什么要求呢？

限制条件

  对于其他非支持向量 $x^{(j)}$ 来说，$x^{(j)}$ 到直线的距离显然是大于支持向量 $x^{(i)}$ 的，所以我们有：

$$d_{x^{(j)}}=\frac{\left|w^T{x}^{(j)}\right|}{|w|}>d_{x^{(i)}}=\frac{1}{|w|}$$

  于是我们有：

$$\left|w^T{x}^{(j)}\right|>1$$

  那么对于所有向量来说：

$$\left|w^{T}x\right|\ge 1$$

  如果把绝对值去掉的话，我们就要分是 $y$ 属于 $1$ 类还是 $-1$ 类了。而经过分类讨论我们会发现，对于所有向量 $x$，我们都有：

$$y^{(i)}[w^T{x}^{(i)}]\ge 1(i=1\sim m)$$

总结

  于是我们可以得到支持向量机想要我们做的事就是这样的：

$$\begin{array}{rl}\underset{w}{\min }\frac{1}{2}& |w|\\ & s.t.y^{(i)}[w^T{x}^{(i)}]\ge 1\end{array}$$