论文标题:TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS
开源代码:https://github.com/Thinklab-SJTU/Crossformer
前言
时间序列分析中,如何有效地建模时序数据中的时间变化是关键,然而直接从一维时序数据提取这种变化很困难。本文提出一种新的时序分析方法——二维变化建模TimesNet。该方法将一维时间序列数据转换为二维张量,作者基于时序数据的多周期性特点,将数据分解为多个周期内变化和周期间变化,并将这些变化分别嵌入到二维张量的列和行中。
这样的好处在于可以利用二维卷积核对这些二维张量进行建模,从而提取出时间序列中更深层次的时间变化特征。基于TimesNet框架,可以自适应地发现时间序列中的多周期性特征,并从转换后的二维张量中提取复杂的时间变化。在五个主流时间序列分析任务中的卓越性能,包括短期和长期预测、插补、分类和异常检测等。与现有方法相比,TimesNet展现出了更高的准确性和稳定性,证明了其在通用时间序列分析中的有效性和通用性。
本文工作
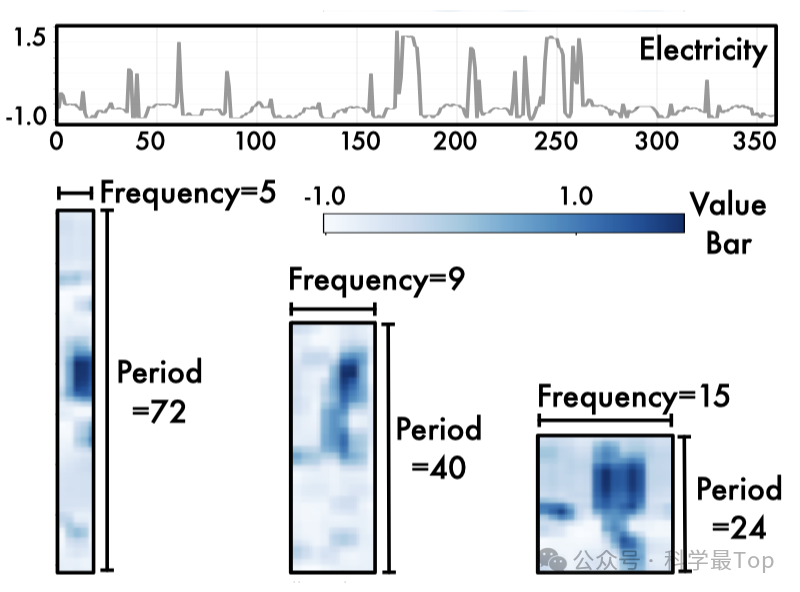
基本观察:如图所示,现实世界中的时间序列通常表现出多周期性,例如天气观测中的日变化和年变化,以及电力消耗中的周变化和季变化。每个时间点的变化不仅受到其相邻区域时间模式的影响,而且与其相邻周期的变化密切相关。作者称之为周期内变化(intraperiod-variation)和周期间变化(interperiod-variation)。前者表示一个周期内的短期时间模式,而后者可以反映连续不同周期的长期趋势。
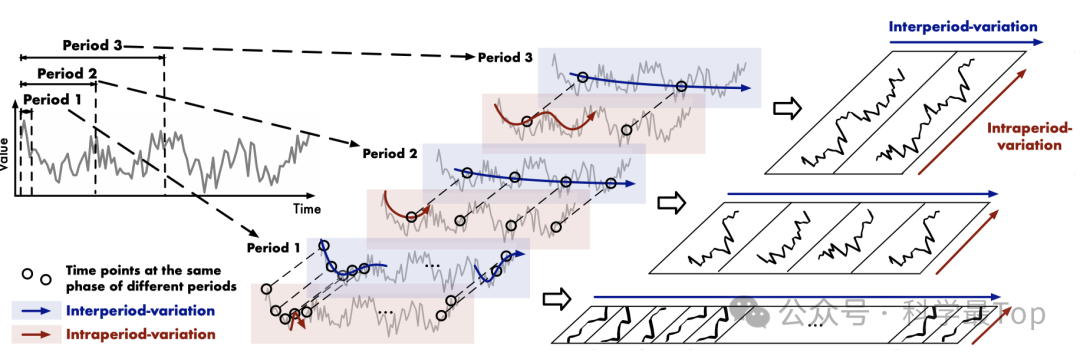
作者基于多个周期将原始的一维时间序列转换为一组二维张量,从而统一了周期内变化和周期间变化。
将一维时序转换为二维时序
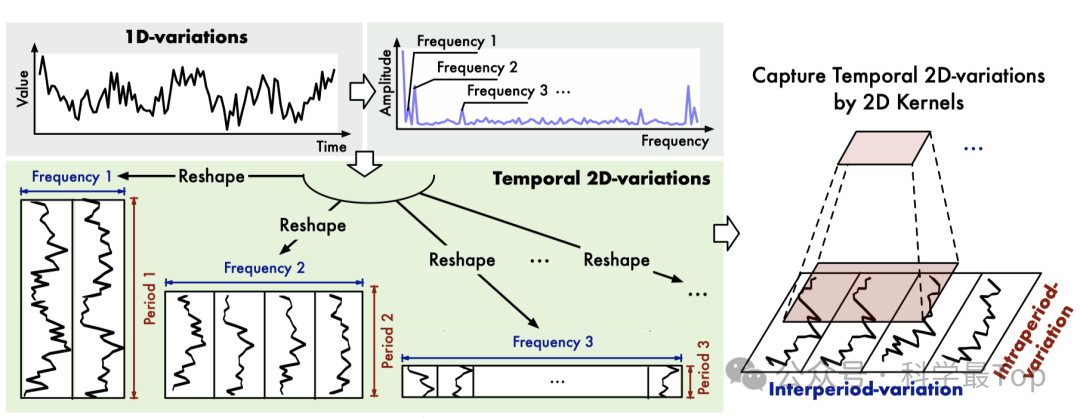
对于长度为T、包含C个变量的时间序列,作者通过快速傅里叶变换(FFT)在频域中分析时间序列,具体如下:
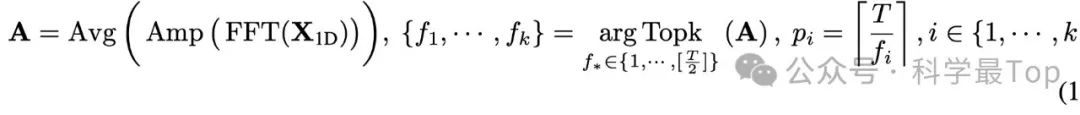
FFT(·) 和 Amp(·) 分别表示快速傅里叶变换和振幅值的计算。A ∈ R^T 表示从C个维度上平均得到的每个频率的振幅。作者只选择前k个振幅值,并获得具有非归一化振幅的{A_f1, ..., A_fk}的最显著频率{f1, ..., fk},其中k是超参数。这些选择的频率也对应于k个周期长度{p1, ..., pk}。上述过程总结如下:

接下来如图以及以下公式所示,我们可以基于选定的周期对原始一维时序数据重塑为多个二维张量。

Padding(·) 是沿着时间维度用零来扩展时间序列,以使其与 Reshape_{p_i, f_i}(·) 兼容,其中 p_i 和 f_i 分别表示转换后的二维张量的行数和列数。
关于使用傅立叶变换分解周期,在ICLR2024还有一篇文章[1],可以看我的另一篇解读。
TimesBlock
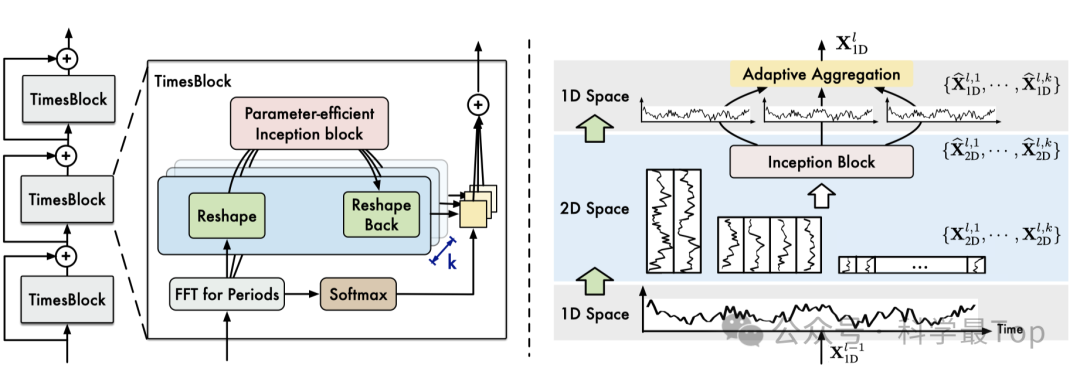
如图所示,TimesNet由堆叠的TimesBlock组成。输入序列首先经过嵌入层得到深度特征,然后对于每一层Times Block通过2D卷积提取而为时序特征。此外,从结构图中还可以看到,作者加了残差连接。
如图3所示,对于第l个TimesBlock,整个过程包括两个连续的部分:捕获时间二维变化模式以及自适应地聚合不同周期下的表示。

-
一维至二维的变换在上一节讲过,如以上公式1-2所示。
-
二维时序特征的提取。作者采用了inception使用2D卷积从这些二维张量中方便地提取出有信息的表示。如公式3。
-
二维至一维的变换。对于提取的时序特征,作者将其转回一维进行信息聚合。如公式4。
自适应融合。融合k个不同的一维表示{X_1, ..., X_k}以供下一层使用。受到自相关(Auto-Correlation)思想的启发,基于幅度来加权求和聚合这些一维表示。
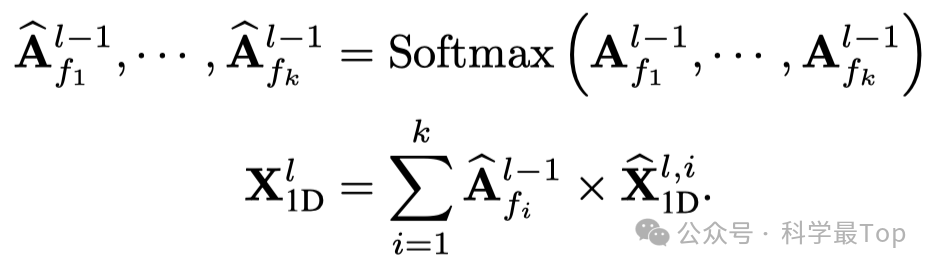
实验与总结
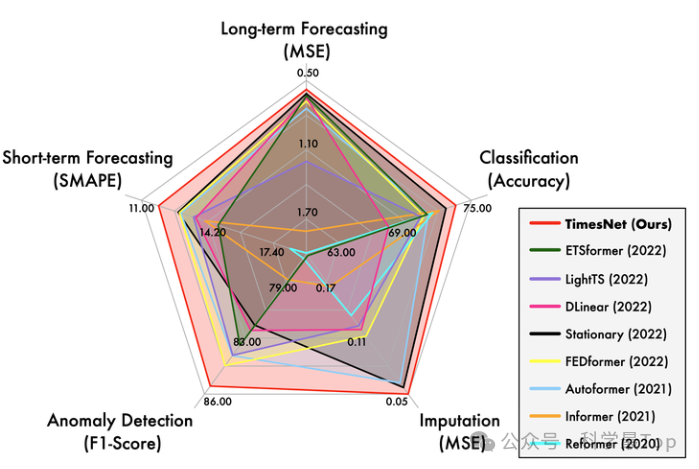
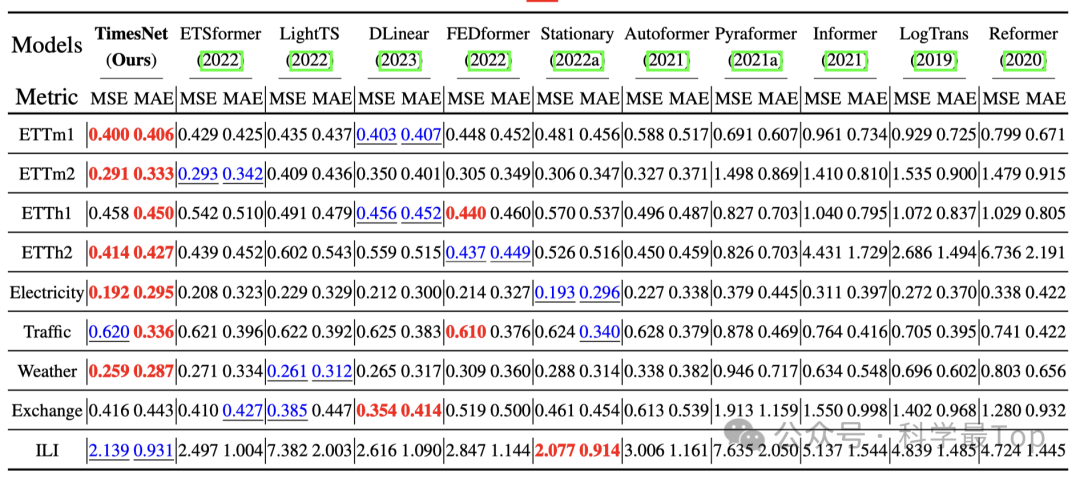
在长时、短时预测、缺失值填补、异常检测、分类五大任务上实现了全面领先。我看知乎对文章的讨论比较激烈,但作者比较耐心的对提出的疑问进行了解答,个人感觉学习解决问题的思路还是非常值得阅读的。另外在写作方面,文章可视化做的非常好,下面的雷达图我已经不止一次看到了。
欢迎大家关注我的公众号【科学最top】,专注于时序高水平论文解读,回复‘论文2024’可获取,2024年ICLR、ICML、KDD、WWW、IJCAI五个顶会的时间序列论文整理列表和原文。