Python用TOPSIS熵权法重构粮食系统及期刊指标权重多属性决策MCDM研究|附数据代码...

原文链接：https://tecdat.cn/?p=37724

在当今世界，粮食系统的稳定性至关重要。尽管现有的全球粮食系统在生产和分配方面表现出较高的效率，但仍存在大量人口遭受饥饿以及诸多粮食安全隐患。与此同时，在学术领域，准确评估情报学期刊的质量和影响力对于学术研究和信息传播意义重大（点击文末“阅读原文”获取完整代码数据）。

本研究旨在通过TOPSIS熵权法、多属性决策(MCDM)方法对全球粮食系统进行重构，以优化其效率、盈利能力、可持续性和公平性。

同时，结合python的代码和数据运用熵权法对情报学期刊的各项指标进行权重计算，为期刊评价提供科学方法。通过对粮食系统的四个程序 —— 生产、分配、加工和销售进行全面评估，我们致力于构建一个更加稳定、可持续且公平的粮食系统。而对于情报学期刊的研究，则有助于提升学术评价的准确性和科学性。

对于粮食系统的重构，我们提出了一系列模型。首先，建立模型 I 说明食物系统的效率和利润；其次，模型 II 衡量粮食系统的可持续性；第三，构建模型 III 证明食品系统中的公平问题。此外，我们还利用熵 topsis 方法评估食物系统的稳定性。对于情报学期刊指标权重的计算，结合python的代码和数据我们采用熵权法，通过对数据的处理和分析，得到了期刊学术质量、期刊影响力和期刊显示度等一级指标的权重。

对于重构粮食系统的建议Re-optimizing Food System

我们的全球粮食系统是不稳定的，即使是在世界上通常服务良好的地区。这些不稳定的部分原因是我们目前庞大的国家和国际粮食生产商和分销商的全球体系。这种粮食系统允许粮食以相对便宜和高效的方式生产和分配，因此表明当前的模式优先考虑效率和盈利能力。

尽管这个系统效率很高，但是全球依然大量人口遭受饥饿，同时存在很多粮食安全隐患

我们希望提出一个模型，重新构想和确定我们食品系统的优先级，以优化效率、盈利能力、可持续性和/或公平性。

解决方案

任务/目标

根据公开数据建立影响产量的原因，粮食生产对环境的影响即可持续性，食品运输过程的损耗和经济消耗，提出对于地区食品分配合理性的指标

问题重述

全球粮食系统由四个程序组成：粮食生产、分配、加工还有销售。我们对食物系统的效率进行了定量和充分的评估以及盈利能力、公平性、可持续性和稳定性，相应的变量侧重于每一个步骤。

•衡量效率和盈利能力

•衡量可持续性

•衡量公平

•变量的比较静态分析

•通过示例测量可伸缩性

模型简述

首先，我们建立模型I来说明食物系统的效率和利润，同时生产、加工和分销，并在ISM模型下进行计算确认。

第二，模型II是用来衡量粮食系统的可持续性，重点是食品系统的环境成本。我们计算出在给定条件下的显式和隐式成本用线性回归分析污染指数。我们可以定量地测量环境质量由食物系统引起的。

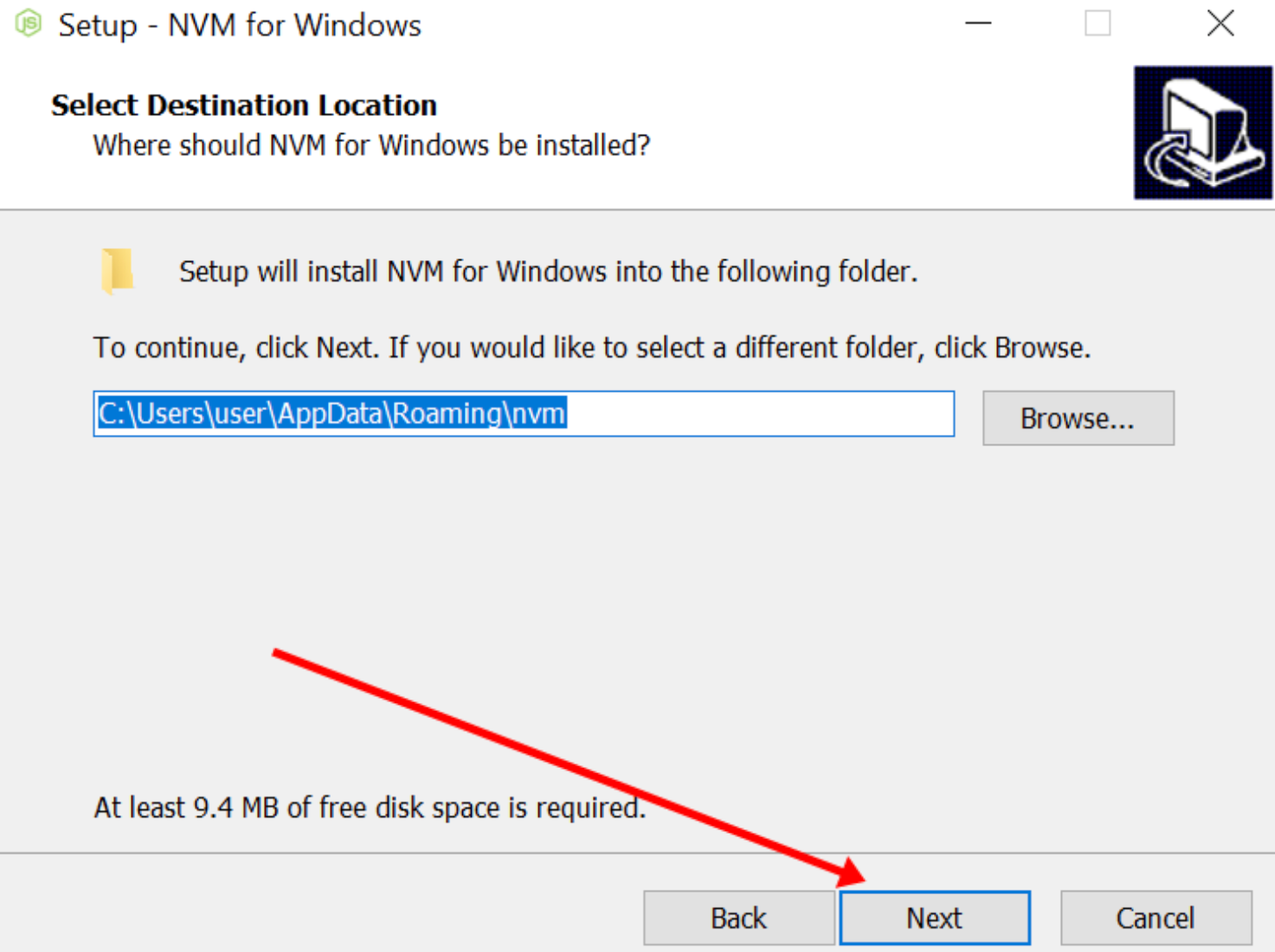
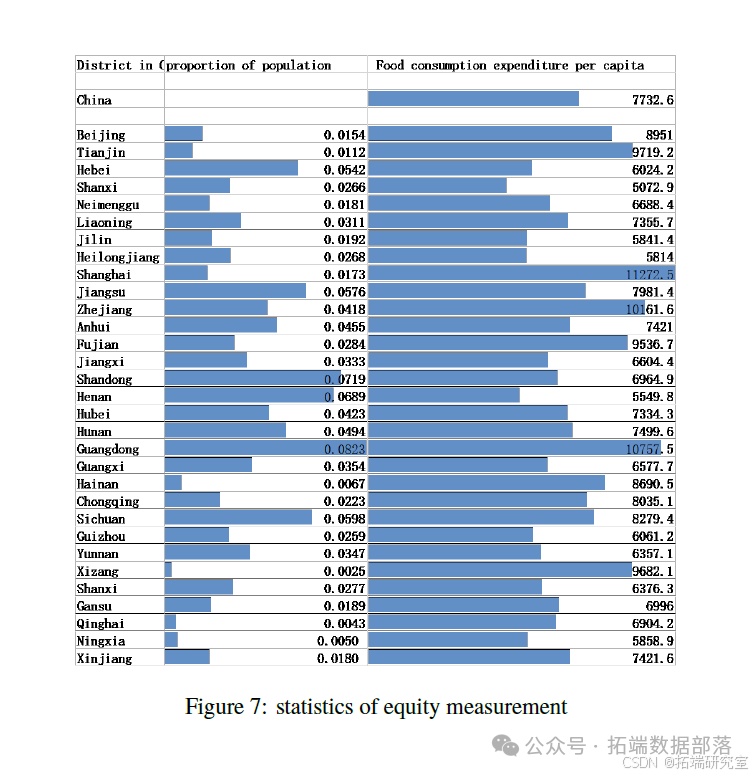
第三，我们构建了模型III，以证明食品系统中的公平问题主要与一个国家的食品支出有关。

此外，我们利用熵topsis方法来评估食物系统，并讨论现有系统在应对某些紧急情况时的稳定性。

部分模型展示如下

基本完成需要完成的任务，该系统可用于世界各地的许多国家，它还强调了利用宏观经济学研究粮食系统公平性和可持续性的意义。这些数据在大多数国家都很常见。如上所述，我们可以到达通过调整生产要素或政府政策进行优化。

提供了一种简化但仍然定量的方法来衡量权益通过收集一个国家内不同人群的数据来计算差异，我们成功地衡量了粮食系统内部的公平水平，并进行了比较静态分析。

但是也存在明显缺点，特别是对于运输方面，我们采用的ISM解释结构模型仅仅能够定性地分析主要影响原因而不能定量分析，而且由于数据的缺乏，仅仅对部分地区较为准确，整个模型比较粗糙。

点击标题查阅往期内容

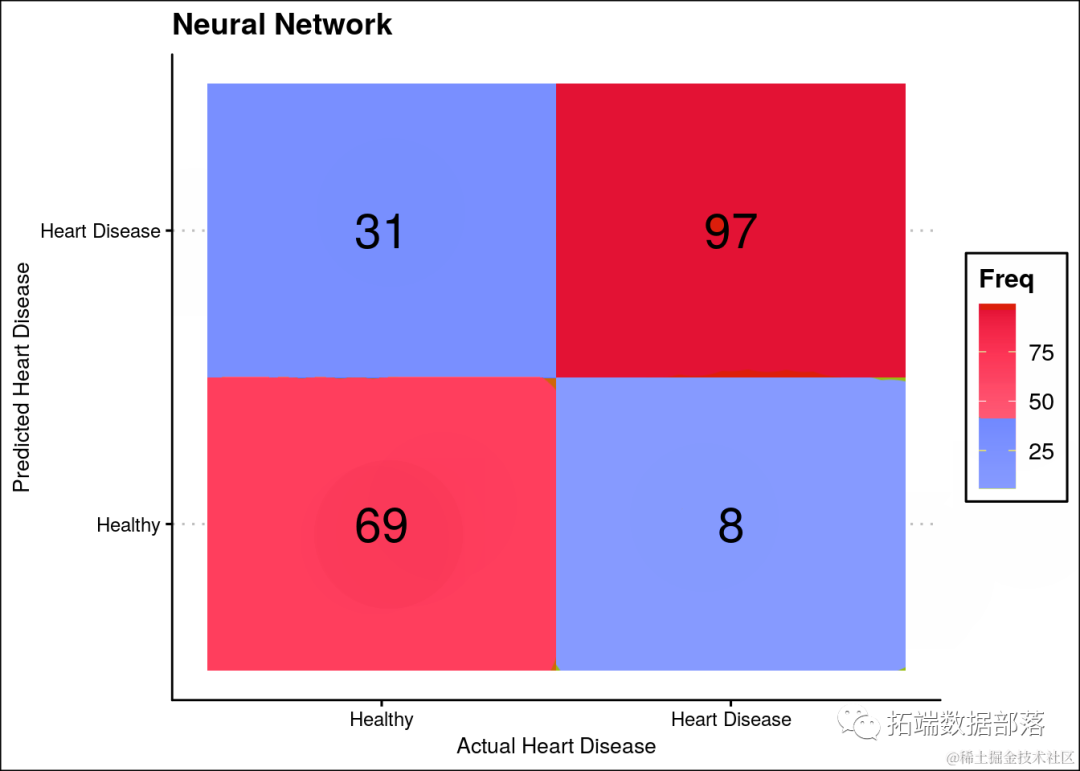
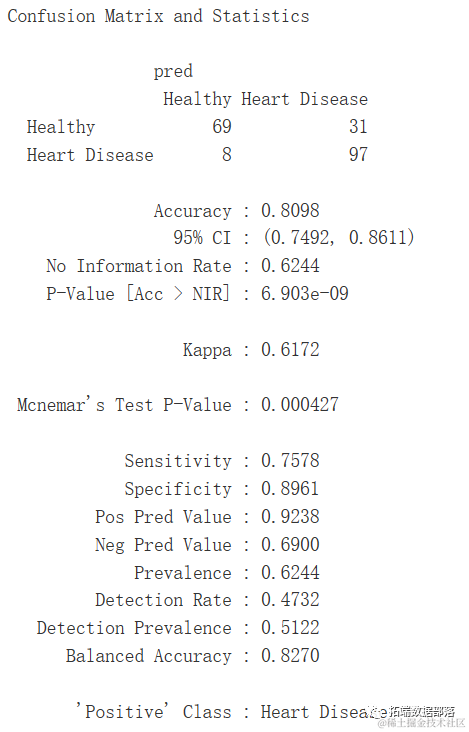
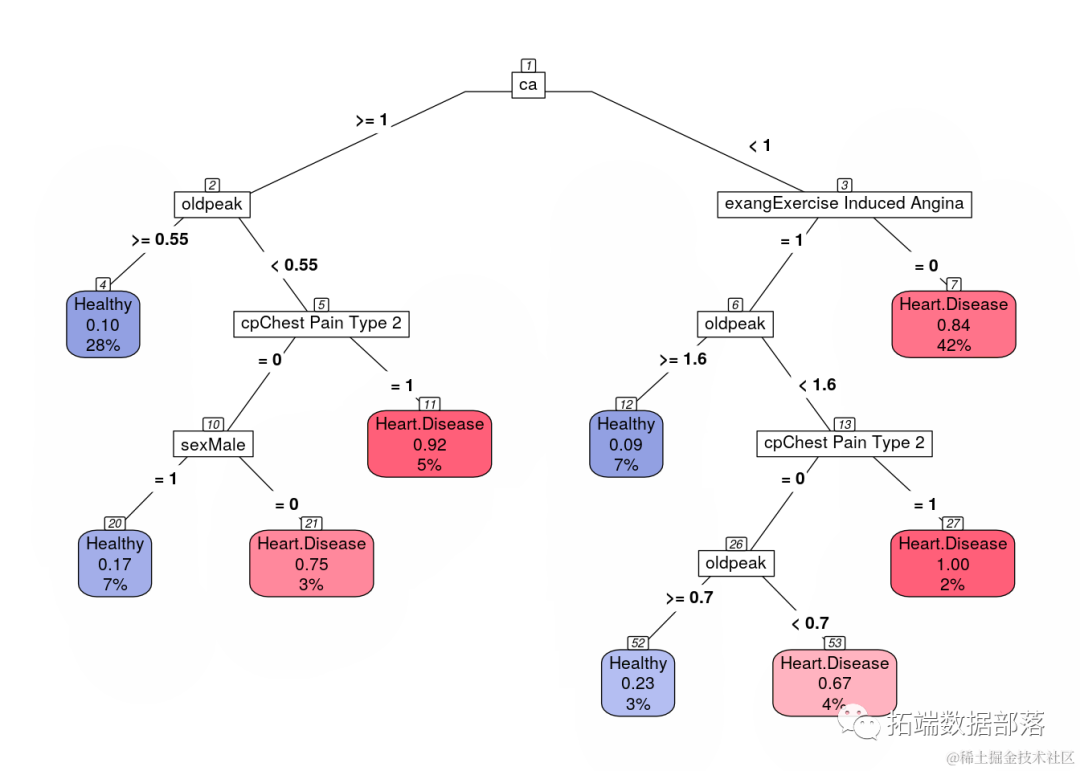
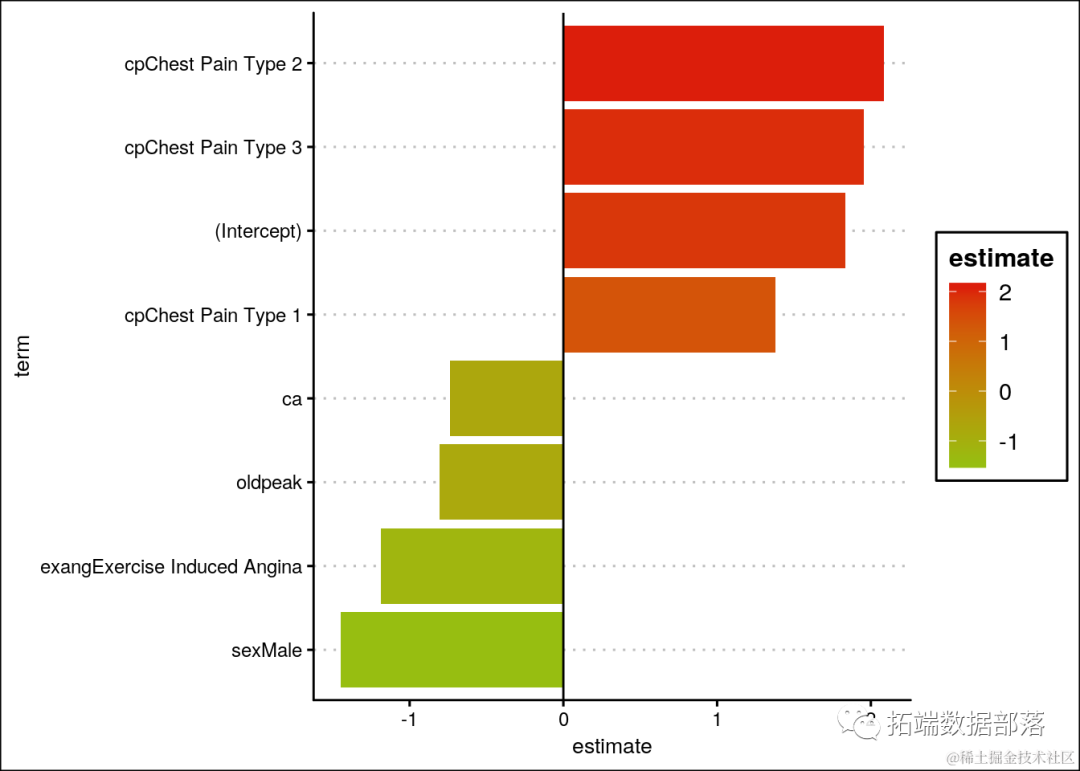
R语言逻辑回归、决策树、随机森林、神经网络预测患者心脏病数据混淆矩阵可视化

左右滑动查看更多

TOPSIS 方法在多属性决策(MCDM)中的应用|附数据代码

逼近理想解排序法（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）在 20 世纪 80 年代作为一种多准则决策方法出现。TOPSIS 选择与理想解的欧氏距离最短且与负理想解的距离最大的方案。

假设你要购买一部手机，去商店后根据 RAM、内存、屏幕尺寸、电池和价格等因素对 5 部手机进行分析。在考虑众多因素后感到困惑，不知如何决定购买哪部手机。TOPSIS 就是一种根据给定因素的权重和影响来分配排名的方法。

权重：表示给定因素应被考虑的程度（默认所有因素权重为 1）。例如，若希望 RAM 的权重高于其他因素，可以将 RAM 的权重设为 2，其他因素设为 1。
影响：指给定因素具有正面或负面的影响。例如，希望电池容量尽可能大，而手机价格尽可能低，所以给电池分配“+”权重，给价格分配“-”权重。

此方法可用于根据各种因素（如相关性、决定系数 $R^2$、准确率、均方根误差等）对机器学习模型进行排名。现在我们已经了解了 TOPSIS 是什么以及可以在哪里应用它。下面来看在给定的由多行（如不同的手机）和多列（如各种因素）组成的数据集上实施 TOPSIS 的步骤。

数据集示例：

给定数据集中特定因素的值被视为标准单位。始终对任何非数字数据类型进行标签编码。

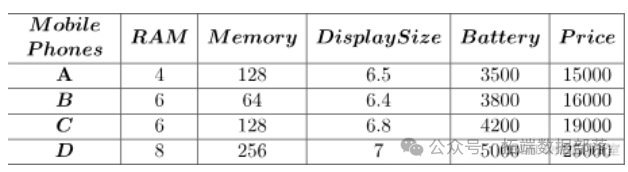
步骤：

步骤 1：计算归一化矩阵和加权归一化矩阵。通过以下方式对每个值进行归一化，其中 $m$ 是数据集中的行数，$n$ 是列数。$i$ 沿行变化，$j$ 沿列变化。

对于上述给定的值，归一化矩阵将是：

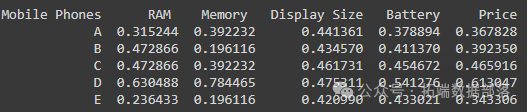
然后，将每列中的每个值与相应的给定权重相乘。

def Normaze(dataset, nCol, weights):for i in range(1, nCol):temp = 0for j in range(len(dataset)):temp = temp + dataset.iloc\[j, i\]\*\*2temp = temp\*\*0.5for j in range(len(dataset)):dataset.iat\[j, i\] = (dataset.iloc\[j, i\] / temp)*weights\[i-1\]print(dataset)

步骤 2：计算理想最优解和理想最劣解以及每行与理想最劣解和理想最优解的欧氏距离。首先，确定理想最优解和理想最劣解：这里需要考虑影响，即它是“+”影响还是“-”影响。如果是“+”影响，那么某一列的理想最优解是该列的最大值，理想最劣解是该列的最小值，反之对于“-”影响则相反。

现在需要计算所有行中的元素与理想最优解和理想最劣解的欧氏距离。这里 $diw$ 是第 $i$ 行的最劣距离计算值，其中 $ti,j$ 是元素值，$tw,j$ 是该列的理想最劣解。类似地，可以找到 $dib$，即第 $i$ 行的最佳距离计算值。

现在，数据集将包含正距离和负距离，如下所示：

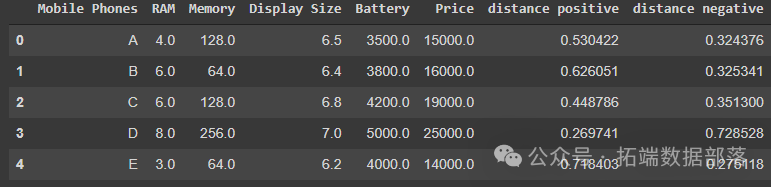
步骤 3：计算 TOPSIS 得分并进行排名。现在我们有了距离正和距离负，让我们根据它们为每行计算 TOPSIS 得分。

TOPSIS 得分 = $diw$ / ($dib$ + $diw$) 对于每一行

现在根据 TOPSIS 得分进行排名，即得分越高，排名越好。

我们的数据集将如下进行排名：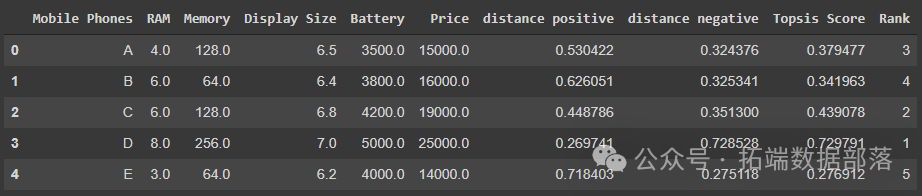

基于熵权法的情报学期刊指标权重计算|附数据代码

本文旨在通过熵权法对情报学期刊的各项指标进行权重计算，以评估不同指标在期刊评价中的重要性。通过对数据的处理和分析，得到了期刊学术质量、期刊影响力和期刊显示度等一级指标的权重。

一、引言

在情报学领域，对期刊的评价是一个重要的研究课题。准确评估期刊的质量和影响力对于学术研究和信息传播具有重要意义。本文采用熵权法对情报学期刊的各项指标进行权重计算，为期刊评价提供一种科学的方法。

二、数据准备

首先，使用pandas库读取情报学期刊数据文件情报学期刊.xlsx。

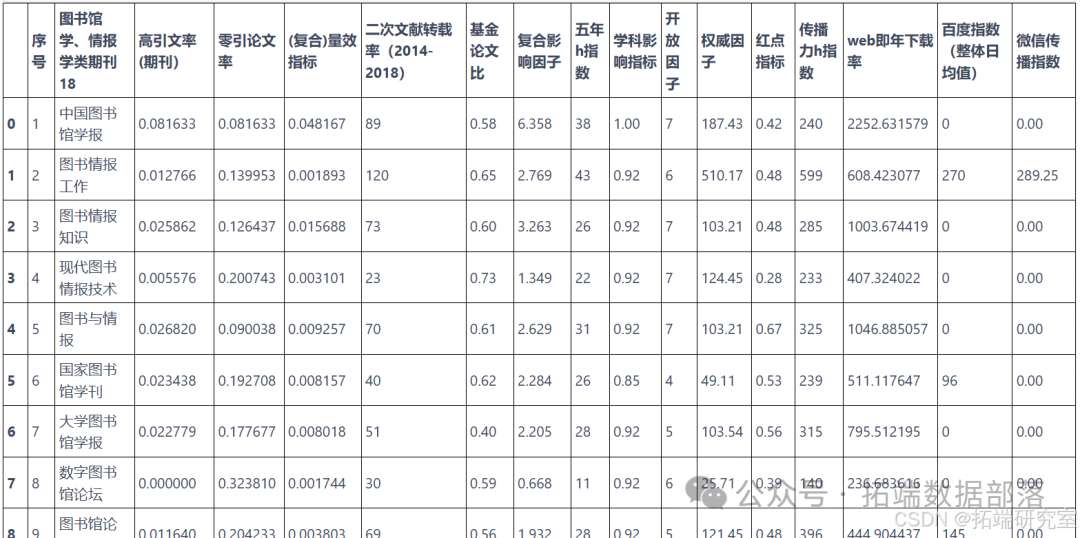
import pandas as pd# 加载Excel文件file\_path = '/mnt/data/核心期刊数据.xlsx'df = pd.read\_excel(file\_path)# 显示数据的前几行以了解其结构df.head()import matplotlib.pyplot as pltimport seaborn as sns# 设置中文字体，以便在图表中显示中文plt.rcParams\['font.sans-serif'\] = \['SimHei'\]plt.rcParams\['axes.unicode\_minus'\] = False# 创建一个画布，包含多个子图fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(15, 15))# 1. 条形图：展示各期刊的“出版文献量”sns.barplot(x='出版文献量', y='期刊名', data=df, ax=axes\[0, 0\])axes\[0, 0\].set\_title('各期刊的出版文献量')# 2. 饼图：展示不同“基金论文比”的分布df\['基金论文比分类'\] = pd.cut(df\['基金论文比'\], bins=\[0, 0.3, 0.6, 1\], labels=\['低', '中', '高'\])fund\_paper\_ratio\_distribution = df\['基金论文比分类'\].value\_counts()axes\[0, 1\].pie(fund\_paper\_ratio\_distribution, labels=fund\_paper\_ratio\_distribution.index, autopct='%1.1f%%')axes\[0, 1\].set\_title('基金论文比分布')# 3. 折线图：展示“综合影响因子”和“复合影响因子”的关系sns.lineplot(x='综合影响因子', y='复合影响因子', data=df, marker='o', ax=axes\[1, 0\])axes\[1, 0\].set\_title('综合影响因子与复合影响因子的关系')# 4. 箱线图：展示“篇均被引”的分布情况sns.boxplot(x=df\['篇均被引'\], ax=axes\[1, 1\])axes\[1, 1\].set\_title('篇均被引的分布情况')# 5. 散点图：展示“出版文献量”与“总被引频次”的关系sns.scatterplot(x='出版文献量', y='总被引频次', data=df, ax=axes\[2, 0\])axes\[2, 0\].set\_title('出版文献量与总被引频次的关系')# 调整布局plt.tight\_layout()plt.show()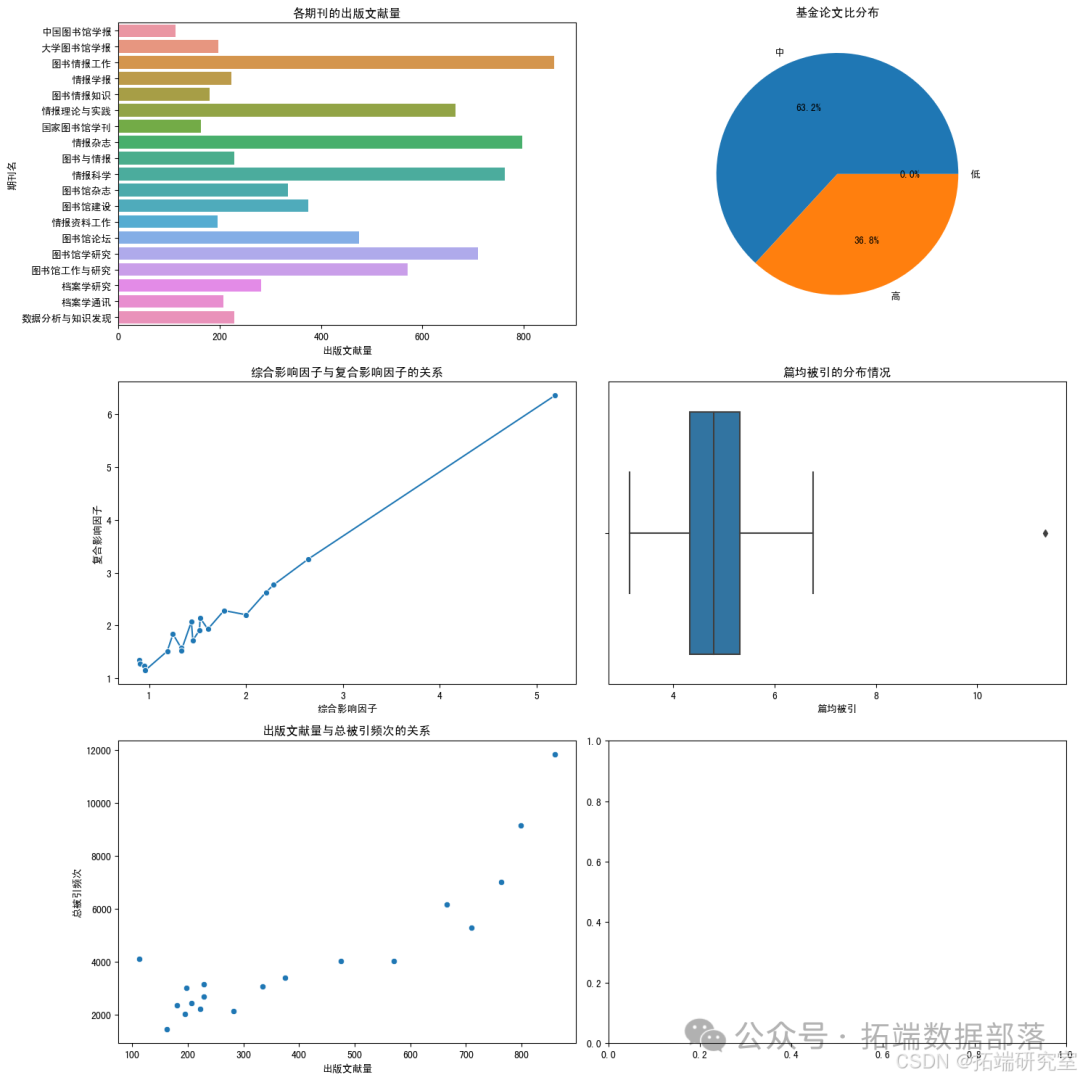

三、指标处理

获取正向指标列表：

# 在没有去掉网络指标的前提下
zhengxiang = data_qingbaoxue.columns.values.tolist()
del zhengxiang\[0:2\]
del zhengxiang\[1\]
zhengxiang  # 获得正向指标的列表

获取负向指标列表：

index = data_qingbaoxue.columns.values.tolist()
del index\[0:2\]
fuxiang = \['零引论文率'\]  # 获得负向指标列表
journal\_name = data\_qingbaoxue\['图书馆学、情报学类期刊18'\]  # 包含了所有需要测量的期刊
indexs = data_qingbaoxue\[index\]  # 包含了需要测量的指标的所有数据

进行数据归一化等操作：

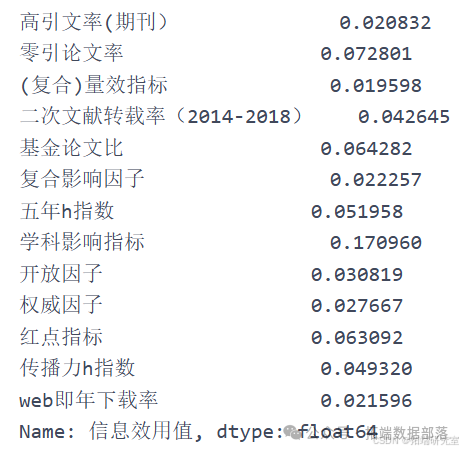
em = EntropyMethod(indexs, fuxiang, zhengxiang, journal_name)
em.uniform()  # 归一化后的数据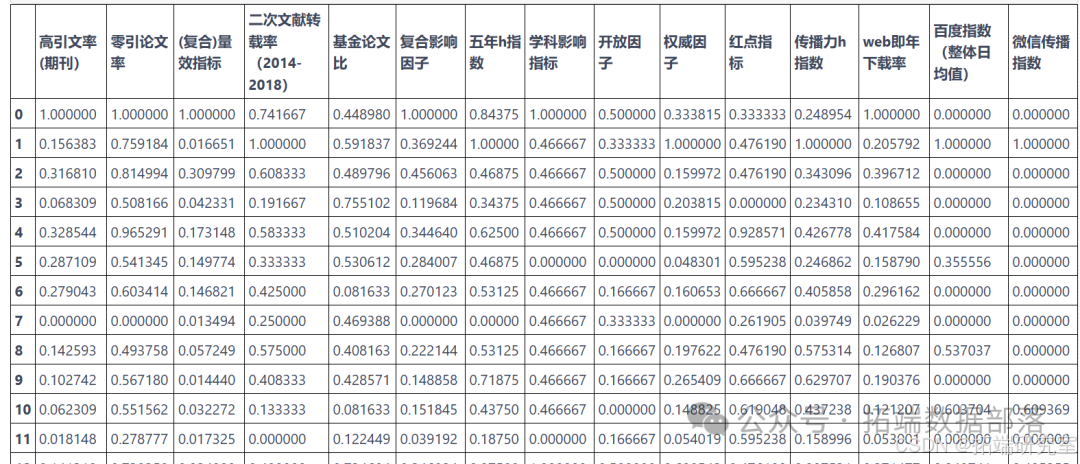

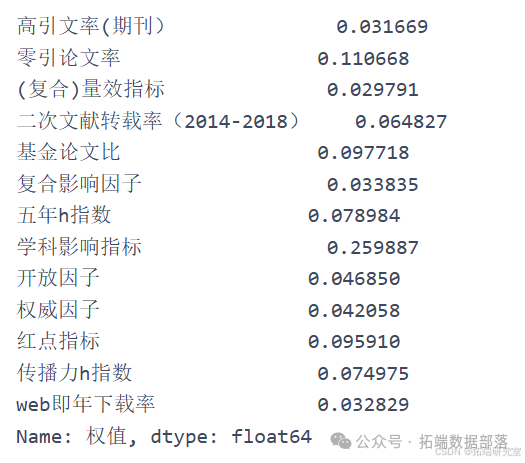
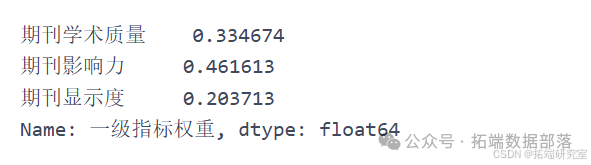
em.calc_probability()
em.calc_entropy()
em.calc\_entropy\_redundancy()  # 尝试计算信息效用值
``````
em.calc_Weight()  # 计算得单项指标最终权重
``````
weight = em.calc_Weight().tolist()
yijizhibiao = \[\]
yijizhibiao.append(sum(weight\[0:5\]))  # 按照分类将单项指标权重相加得一级指标权重
yijizhibiao.append(sum(weight\[5:10\]))
yijizhibiao.append(sum(weight\[10:\]))
yijizhibiao = pd.Series(yijizhibiao, index=\['期刊学术质量', '期刊影响力', '期刊显示度'\], name='一级指标权重')
yijizhibiao  # 计算一级指标权重

去除网络指标后再次计算：

# 在删除网络指标的前提下
zhengxiang.pop()
zhengxiang.pop()  # 删除位于尾部的两个网络指标
positive = zhengxiang
``````
negative = fuxiang
index.pop()
index.pop()  # 同样是删除位于尾部的两个网络指标
indexs = data_qingbaoxue\[index\]
em = EntropyMethod(indexs, positive, negative, journal_name)
``````
em.uniform()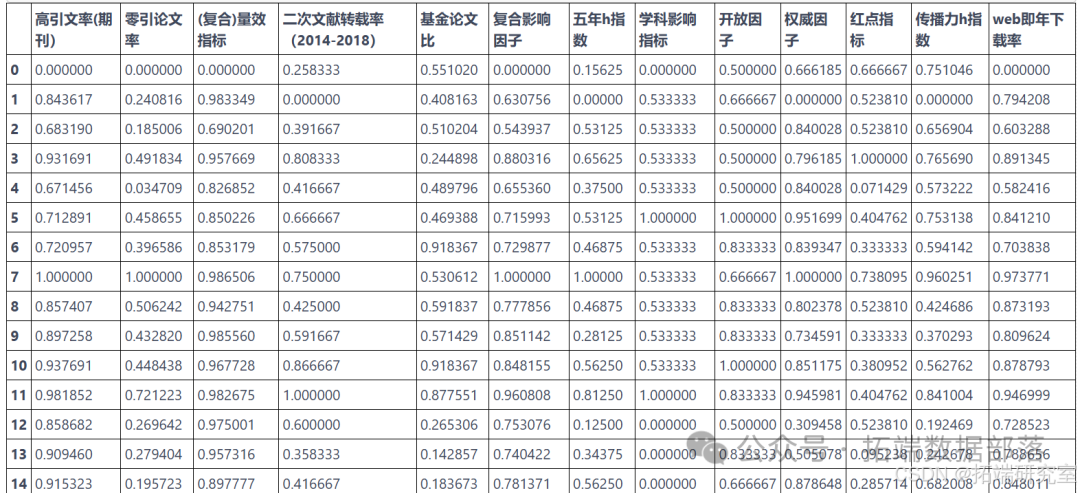

em.calc_probability()
em.calc_entropy()
em.calc\_entropy\_redundancy()  # 尝试计算信息效用值
``````
em.calc_Weight()  # 计算得单项指标最终权重
``````
weight = em.calc_Weight().tolist()
yijizhibiao = \[\]
yijizhibiao.append(sum(weight\[0:5\]))
yijizhibiao.append(sum(weight\[5:10\]))
yijizhibiao.append(sum(weight\[10:\]))
yijizhibiao = pd.Series(yijizhibiao, index=\['期刊学术质量', '期刊影响力', '期刊显示度'\], name='一级指标权重')
yijizhibiao  # 计算一级指标权重