1. 力扣99:恢复二叉搜索树
1.1 题目:
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例 1:

输入:root = [1,3,null,null,2] 输出:[3,1,null,null,2] 解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:

输入:root = [3,1,4,null,null,2] 输出:[2,1,4,null,null,3] 解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
- 树上节点的数目在范围
[2, 1000]内 -231 <= Node.val <= 231 - 1
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗?
1.2 思路:
使用两次dfs遍历,然后调库排序,然后输出到树中。时间复杂度为O(n*logn),是由于调库的排序方法的时间复杂度是O(n*logn)。空间复杂度是O(n),因为使用了跟树节点大小的列表空间。
1.3 题解:
class Solution {int k;List<Integer> list = new LinkedList<>();public void recoverTree(TreeNode root) {dfs1(root);Collections.sort(list);dfs2(root);}private void dfs1(TreeNode node) {if(node == null) return;dfs1(node.left);list.add(node.val);dfs1(node.right);}private void dfs2(TreeNode node) {if(node == null) return;dfs2(node.left);node.val = list.get(k++);dfs2(node.right);}
}2. 力扣1305:两棵二叉树中的所有元素
2.1 题目:
给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含 两棵树 中的所有整数并按 升序 排序。.
示例 1:
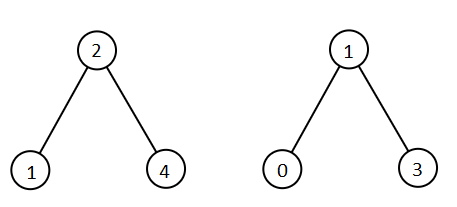
输入:root1 = [2,1,4], root2 = [1,0,3] 输出:[0,1,1,2,3,4]
示例 2:
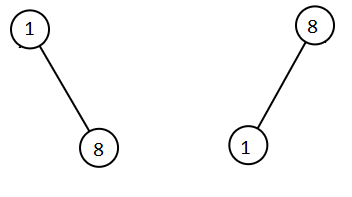
输入:root1 = [1,null,8], root2 = [8,1] 输出:[1,1,8,8]
提示:
- 每棵树的节点数在
[0, 5000]范围内 -105 <= Node.val <= 105
2.2 思路:
把两个树中所有的节点的值都放进了一个列表,排序以后返回。
2.3 题解:
class Solution {List<Integer> list = new LinkedList<>();public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {dfs(root1);dfs(root2);Collections.sort(list);return list;}private void dfs(TreeNode node) {if (node == null) return;dfs(node.left);list.add(node.val);dfs(node.right);}
}3. 力扣 230:二叉搜索树中的第k小的元素
3.1 题目:
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。
示例 1:
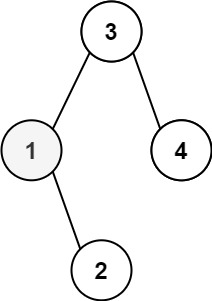
输入:root = [3,1,4,null,2], k = 1 输出:1
示例 2:
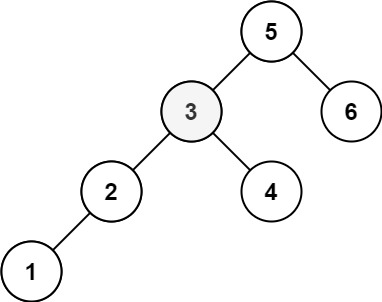
输入:root = [5,3,6,2,4,null,null,1], k = 3 输出:3
提示:
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
3.2 思路:
dfs中序遍历,默认有序,直接返回第k个元素。
3.3 题解:
class Solution {List<Integer> list = new ArrayList<>();public int kthSmallest(TreeNode root, int k) {dfs(root);return list.get(k-1);}private void dfs(TreeNode node) {if(node == null) return;dfs(node.left);list.add(node.val);dfs(node.right);}
}3.4 思路:
用栈代替dfs递归,使用迭代的方法。
3.5 题解:
class Solution {// 使用栈代替了dfs迭代Deque<TreeNode> stack = new LinkedList<>();public int kthSmallest(TreeNode root, int k) {TreeNode cur = root;int n = 0;// 手写了一个中序遍历while(cur != null || !stack.isEmpty()){if(cur != null){stack.push(cur);cur = cur.left;}else{// pop的顺序是有序的,所以代码在这加以判断n++;if(n == k){return stack.peek().val;}cur = stack.pop();cur = cur.right;}}return 0;}
}4. 力扣897:递增顺序搜索树
4.1 题目:
给你一棵二叉搜索树的 root ,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:

输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:

输入:root = [5,1,7] 输出:[1,null,5,null,7]
提示:
- 树中节点数的取值范围是
[1, 100] 0 <= Node.val <= 1000
4.2 思路:
当成插入链表题来解决。中序遍历得到node节点,然后插入到递增的顺序链表中。并实时更新cur节点。
4.3 题解:
class Solution {// 把树变成链表TreeNode dummy = new TreeNode(10086, null, null);TreeNode cur = dummy;public TreeNode increasingBST(TreeNode root) {dfs(root);return dummy.right;}private void dfs(TreeNode node){if(node == null) return;dfs(node.left);cur.right = node;// 递归到这说明该node节点的左子树已经全遍历完,并加入到链表了// 可以设置为null了node.left = null;// 更新cur指针cur = node;dfs(node.right);}
}