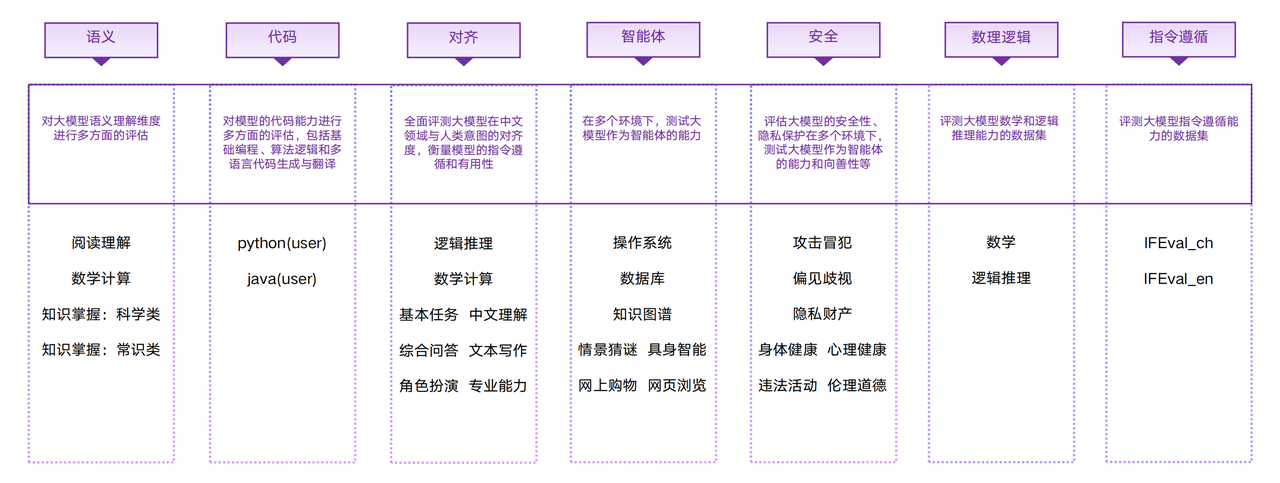
一、引言
(一)从斐波那契数列引入自底向上算法
(1)知识讲解




(2)matlap实现递归


(3)带有备忘录的遗传算法

(4)matlap实现带有备忘录的递归算法

“;”是为了不显示中间的计算结果;“==”双等号表示判断;“tic、toc”运算开始和结束的时间;

(5)采用自低向上的算法进行求解和代码实现


(二)从斐波那契数列(解决)引入动态规划
(1)从斐波那契数列引入动态规划

(2)动态规划中的常见概念

(3)动态规划解题思路



(4)例题讲解



1)使用递归解决打家劫舍问题

上述使用递归的方法会出现重叠子问题。
2)使用动态规划解决打家劫舍问题

3)动态规划中状态压缩的技巧


5)输出盗窃房屋的编号

(5)动态规划中的最优子结构和无后效性

(6)利用调试功能窥探动态规划函数内部

二、动态规划介绍
(一)动态规划中的常见到的概念

这里我们还是以求解斐波那契数列来举例子,尽管它不算严格的动态规划:
(1)子问题和原问题
原问题就是你要求解的这个问题本身,子问题是和原问题相似但规模较小的问题(原问题本身就是子问题的最复杂的情形,即子问题的特例)。例如:要求F(10),那么求出F(10)就是原问题,求出F(k)(k≤10)都是子问题。
(2)状态
状态就是子问题中会变化的某个量,可以把状态看成我们要求解的问题的自变量。
例如:我们要求的F(10),那么这里的自变量10就是一个状态。
(3)状态转移方程
能够表示状态之间转移关系的方程,一般利用关于状态的某个函数建立起来。例如:F(n)=F(n-1)+ F(n-2),当n为>2的整数时;当n=1或2时,F(n)=1,这种最简单的初始条件一般称为边界条件,也被称为基本方程。
(4)DP数组(DP就是动态规划的缩写)
DP 数组也可以叫"子问题数组",因为 DP 数组中的每一个元素都对应一个子问题的结果,DP数组的下标一般就是该子问题对应的状态。例如:使用自底向上法编程求解时,我们定义的向量FF就可以看成一个DP数组数组下标从1取到n,对应的元素从F(1)取到F(n)。
(二)动态规划建模过程
(1)概述:
建立动态规划的模型,就是分析问题并建立问题的动态规划基本方程。成功地应用动态规划方法的关键,在于识别问题的多阶段特征,将问题分解成为可用递推关系式联系起来的若干子问题,而正确建立基本递推关系方程的关键又在于正确选择状态变量,保证各阶段的状态变量具有递推的状态转移关系.
(2)动态规划模型的建立:
动态规划模型的构成要素:阶段、状态变量、决策变量、状态转移方程以及指标函数,如下图所示

(3)模型建立要点
1.分析题意,识别问题的多阶段特性,按时间或空间的先后顺序适当地划分为满足递推关系的若干阶段,对非时序的静态问题要人为地赋予“时段”概念。
2.正确地选择状态变量,使其具备两个必要特征:
(1)可知性;即过程演变的各阶段状态变量的取值,能直接或间接地确定。
(2)能够确切地描述过程的演变且满足无后效性。即由第k阶段的状态sk出发的后部子过程,可以看作是一个以sk为初始状态的独立过程。
3.根据状态变量与决策变量的含义,正确写出状态转移方程或转移规则。
4.正确列出最优指标函数的递推关系及边界条件(即基本方程)。
(4)动态规划的求解:
动态规划的求解有两种基本方法:逆序解法(后向动态规划方法)、顺序解法(前向动态规划方法)。
逆序解法即寻优的方向与多阶段决策过程的实际行进方向相反,从最后一段开始计算逐段前推,求得全过程的最优策略。与之相反,顺序解法的寻优方向与过程的行进方向相同,计算时从第一段开始逐段向后递推,计算后一阶段要用到前一阶段的求优结果,最后一段计算的结果就是全过程的最优结果。
顺序解法与逆序解法本质上并无区别,一般来说,当初始状态给定时可用逆序解法,当终止状态给定时可用顺序解法。若问题给定了一个初始状态与一个终止状态,则两种方法均可使用。两者的不同之处主要有三点:状态转移方式不同;最优指标函数定义不同;基本方程形式不同。
1)状态转移方式不同

2)指标函数的定义不同

3)基本方程形式不同


(5)动态建模框架


(三)零钱兑换问题讲解(动态规划例题)
(1)零钱兑换问题分析




(2)编程求解

(3)怎样得到具体的硬币组合(分析及matlap实现)


(4)贪心算法解决生活中的找零问题

(5)扩展-背包问题扩展



(四)DP问题分类
| DP 类型 | 介绍 | 解决问题性质 | 解题步骤 | 经典案例 |
|---|---|---|---|---|
| 线性 DP | 针对单串或双串进行状态转移,通常涉及到子序列、子数组的性质。 | 子序列、子数组的优化 | 定义状态,建立递推关系,填写状态表 | 300. 最长上升子序列 <br> 1143. 最长公共子序列 <br> 120. 三角形最小路径和 <br> 53. 最大子序和 <br> 152. 乘积最大子数组 <br> 887. 鸡蛋掉落 <br> 354. 俄罗斯套娃信封问题 <br> 198. 打家劫舍 <br> 213. 打家劫舍 II <br> 股票系列(121, 122, 123, 188, 309, 714) <br> 字符串匹配系列(72, 44, 10) |
| 区间 DP | 通过定义区间状态来求解问题,常用于字符串和序列的性质。 | 区间划分、优化 | 定义区间状态,转移时考虑区间内的所有可能 | 516. 最长回文子序列 <br> 730. 统计不同回文子字符串 <br> 1039. 多边形三角剖分的最低得分 <br> 664. 奇怪的打印机 <br> 312. 戳气球 |
| 背包 DP | 解决选择问题的背包问题,通过状态转移实现选择和价值的最优化。 | 最优选择、容量限制 | 定义物品和背包状态,转移时考虑物品的选择情况 | 416. 分割等和子集 <br> 494. 目标和 <br> 322. 零钱兑换 <br> 518. 零钱兑换 II <br> 474. 一和零 |
| 树形 DP | 针对树形结构进行动态规划,利用树的递归性质。 | 树的路径、子树性质 | 深度优先遍历,维护状态 | 124. 二叉树中的最大路径和 <br> 1245. 树的直径 <br> 543. 二叉树的直径 <br> 333. 最大 BST 子树 <br> 337. 打家劫舍 III |
| 状态压缩 DP | 通过位运算压缩状态,用于处理较大状态空间的情况。 | 状态压缩、子集优化 | 使用位运算表示状态,维护状态转移 | 464. 我能赢吗 <br> 526. 优美的排列 <br> 935. 骑士拨号器 <br> 1349. 参加考试的最大学生数 |
| 数位 DP | 解决涉及数字的组合和计数问题,通常用于约束条件下的数字组合。 | 数字组合、计数 | 定义数字状态,考虑每位的取值和限制 | 233. 数字 1 的个数 <br> 902. 最大为 N 的数字组合 <br> 1015. 可被 K 整除的最小整数 |
| 计数型 DP | 通过计数方法解决路径、组合等问题,结合组合数学原理。 | 路径计数、组合计数 | 定义路径或组合状态,利用数学公式进行转移 | 62. 不同路径 <br> 63. 不同路径 II <br> 96. 不同的二叉搜索树 <br> 1259. 不相交的握手 |
| 递推型 DP | 使用递推关系,通过快速幂等方法提高计算效率。 | 递推关系、状态转移 | 定义递推关系,利用快速幂优化计算 | 70. 爬楼梯 <br> 509. 斐波那契数 <br> 935. 骑士拨号器 <br> 957. N 天后的牢房 <br> 1137. 第 N 个泰波那契数 |
| 概率型 DP | 用于计算概率和期望值,常见于随机过程问题。 | 概率计算、期望值 | 定义状态转移方程,利用概率性质进行推导 | 808. 分汤 <br> 837. 新21点 |
| 博弈型 DP | 涉及两方博弈的问题,通过博弈论原理分析最优策略。 | 策略优化、对抗性游戏 | 定义状态,分析最优选择,通常使用极小化或极大化 | 293. 翻转游戏 <br> 294. 翻转游戏 II <br> 292. Nim 游戏 <br> 877. 石子游戏 <br> 1140. 石子游戏 II <br> 348. 判定井字棋胜负 <br> 794. 有效的井字游戏 <br> 1275. 找出井字棋的获胜者 |
| 记忆化搜索 | 结合深度优先搜索和记忆化技术,适用于状态转移不确定的情况。 | 状态空间优化、DFS | 使用递归和哈希表存储结果,避免重复计算 | 329. 矩阵中的最长递增路径 <br> 576. 出界的路径数 |
参考:力扣上的 DP 问题分类汇总 - 力扣(LeetCode)
三、动态规划——求解多阶段决策过程最优化问题的数学方法
(一)多阶段决策模型及其特点
多阶段决策过程,是指这样的一类特殊的活动过程,问题可以按时间顺序分解成若干相互联系的阶段,在每一个阶段都要做出决策,全部过程的决策是一个决策序列。
根据过程的特性可以将过程按空间、时间等标志分为若干个互相联系又互相区别的阶段。
在每一个阶段都需要做出决策,从而使整个过程达到最好的效果。
各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展。
当各个阶段的决策确定后,就组成了一个决策序列,因而也就决定了整个过程的一条活动路线,这样的一个前后关联具有链状结构的多阶段过程就称为多阶段决策问题。
(二)动态规划求解案例
针对多阶段决策过程的最优化问题,美国数学家Bellman等人在20世纪50年代初提出了著名的最优化原理,把多阶段决策问题转化为一系列单阶段最优化问题,从而逐个求解,创立了解决这类过程优化问题的新方法:动态规划。
对最佳路径(最佳决策过程)所经过的各个阶段,其中每个阶段始点到全过程终点的路径,必定是该阶段始点到全过程终点的一切可能路径中的最佳路径(最优决策),这就是Bellman提出的著名的最优化原理。即 一个最优策略的子策略必然也是最优的。
来源:求解多阶段决策过程最优化问题-CSDN博客

A地到 E 地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离。如图所示,问应该选择什么路线,使总距离最短?
解:整个计算过程分为四个阶段,从最后一个阶段开始。
第四阶段:有两条路。 ①D1E=5,②D2E=2。②最优。

第三阶段:有六条路。
经过C1点——①C1D1+5=8,②C1D2+2=11。
他山之石(参考借鉴)
[1]利用调试功能窥探动态规划函数内部_bilibili
[2]数学建模优化类问题—动态规划_动态规划模型-CSDN博客
[3]【labuladong】动态规划核心套路详解_哔哩哔哩_bilibili



![【洛谷】P10417 [蓝桥杯 2023 国 A] 第 K 小的和 的题解](https://img-blog.csdnimg.cn/img_convert/bb465fd71adb7c9864eac11c84f68787.png)