
摘要
本研究利用人工生态系统优化算法(AEO)解决二维路径规划问题。该算法通过模拟生物种群之间的协作与竞争行为,探索最优路径。实验结果显示,AEO算法能够在复杂环境中有效规划出最优路径,并在收敛速度和解的质量方面具有竞争力。通过一系列仿真实验验证了该算法的有效性和鲁棒性。
理论
人工生态系统优化算法是一种基于生物种群生态学的启发式算法。该算法模仿了不同物种之间的协同作用、竞争以及资源利用的动态过程。在路径规划问题中,AEO算法通过模拟个体(即候选解)之间的相互作用来迭代寻找全局最优解。每一代个体的适应度由其路径的质量(例如路径长度、障碍物避让等)来评估。随着迭代的进行,群体逐渐趋向最优路径。
AEO算法的基本步骤:
-
种群初始化:在搜索空间中随机生成一组候选路径。
-
适应度计算:基于路径长度、障碍物等因素对每条路径进行打分。
-
生物交互:通过竞争、合作、遗传操作等机制优化群体中的个体。
-
收敛判断:当满足终止条件(如最大代数或收敛精度)时,输出最优解。
实验结果
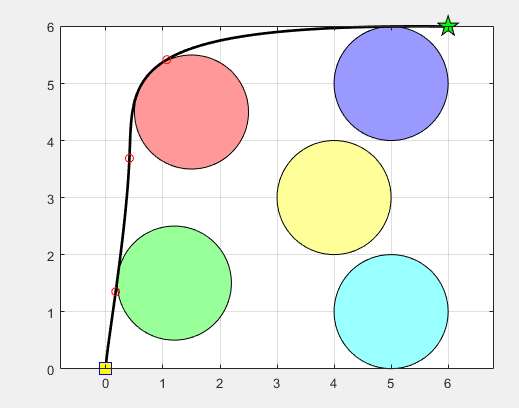
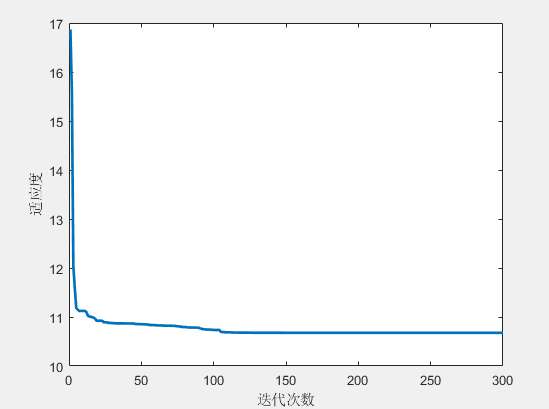
通过仿真平台对AEO算法进行验证,并与传统优化算法进行对比。实验中的场景包含多个障碍物,目标是从起始点规划到目标点的最短路径。第一张图显示了AEO算法在一个二维平面中规划的路径,路径成功避开障碍物并达到目标。第二张图展示了算法在运行过程中收敛的情况,从图中可以看出,算法在早期迅速降低适应度值,之后趋于平稳,表明路径质量趋于最优。
部分代码
% 参数初始化
N = 100; % 种群大小
max_iterations = 300; % 最大迭代次数
population = rand(N, 2); % 随机初始化种群,每个个体有二维坐标% 适应度计算函数(自定义适应度函数,根据问题需求编写)
function fitness = calculate_fitness(population)% 在这里定义适应度函数, 比如路径长度或者障碍物避免fitness = sum(population.^2, 2); % 假设一个简单的目标函数,平方和最小化
end% 选择操作
function selected_population = selection(population, fitness)% 使用轮盘赌法选择个体,或其他选择机制[~, idx] = sort(fitness); % 根据适应度排序selected_population = population(idx(1:round(end/2)), :); % 选择前半部分个体
end% 交叉与变异操作
function new_population = crossover_and_mutation(selected_population)num_selected = size(selected_population, 1);new_population = selected_population;% 交叉操作for i = 1:2:num_selected-1crossover_point = randi([1, 2], 1); % 随机选择交叉点new_population(i, crossover_point:end) = selected_population(i+1, crossover_point:end);new_population(i+1, crossover_point:end) = selected_population(i, crossover_point:end);end% 变异操作mutation_rate = 0.1; % 变异概率mutation_mask = rand(size(new_population)) < mutation_rate;new_population(mutation_mask) = rand(sum(mutation_mask(:)), 1); % 随机变异
end% 判断是否收敛
function is_converged = has_converged(population)% 根据问题需求定义收敛条件,例如适应度变化小于某个阈值if var(population(:)) < 1e-5is_converged = true;elseis_converged = false;end
end% 主算法循环
for iteration = 1:max_iterations% 计算适应度fitness = calculate_fitness(population);% 选择最优个体selected_population = selection(population, fitness);% 交叉与变异new_population = crossover_and_mutation(selected_population);% 更新种群population = new_population;% 判断是否满足收敛条件if has_converged(population)disp(['算法在迭代次数: ', num2str(iteration), '时收敛']);break;end
end参考文献
❝
Glover, F., & Laguna, M. (1998). Tabu Search. Kluwer Academic Publishers.
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, Vol.4, pp. 1942-1948.
Dorigo, M., & Gambardella, L. M. (1997). Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Transactions on Evolutionary Computation, 1(1), 53-66.




















