
摘要
本文基于四旋翼无人机设计与控制,提出了一种结合PID控制、积分滑模控制以及积分反步控制的轨迹跟踪算法。该算法通过调节无人机的运动轨迹,提升其在复杂环境下的稳定性与抗扰动能力。实验结果表明,该算法能有效改善无人机的轨迹跟踪精度,并在多个自由度上均取得了较好的控制效果。
理论
1. PID 控制理论
PID 控制是一种广泛应用于控制系统中的经典控制方法。它通过对误差信号进行比例 (P)、积分 (I)、微分 (D) 操作,调节系统输出达到期望目标值。PID 控制器的数学表达式为:
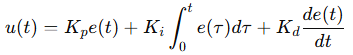
其中,𝑒(𝑡) 为误差, 𝐾𝑝 、𝐾𝑖 、𝐾𝑑分别为比例、积分和微分增益。
2. 积分滑模控制理论
积分滑模控制是一种增强系统鲁棒性的控制策略,滑模面可以设定为:
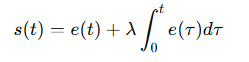
该控制策略可以有效减小外界干扰对系统的影响,且具有较强的自适应性。
3. 积分反步控制理论
积分反步控制通过引入虚拟控制量,分步解决系统控制问题。其主要思想是对系统进行逐步反馈线性化,使其满足 Lyapunov 稳定条件,从而实现系统稳定性。
实验结果
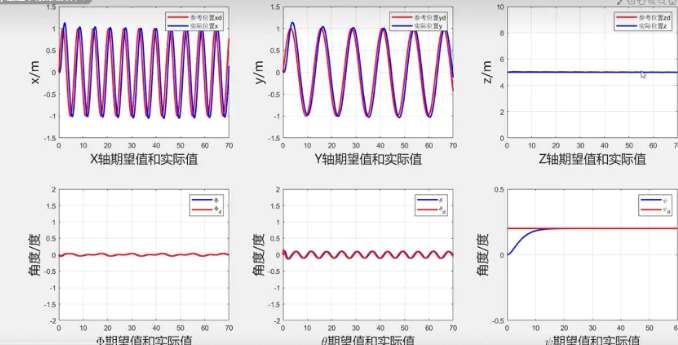
通过仿真实验对四旋翼无人机的轨迹跟踪效果进行验证,结果如图所示。图中的六个子图分别展示了无人机在 X 轴、Y 轴、Z 轴的位移变化以及三个角度自由度上的角度变化。实验对比了实际轨迹与期望轨迹(蓝色与红色曲线),结果表明,该控制算法能够较好地实现期望轨迹的跟踪效果,特别是在X和Y方向上的振荡情况得到了有效控制。
部分代码
% PID控制参数
Kp = [1.5, 1.5, 1.5]; % 比例增益
Ki = [0.1, 0.1, 0.1]; % 积分增益
Kd = [0.2, 0.2, 0.2]; % 微分增益% 时间设置
t = 0:0.1:70;% 期望轨迹
x_d = sin(0.1*t);
y_d = sin(0.1*t);
z_d = zeros(size(t));% 实际轨迹初始化
x_real = zeros(size(t));
y_real = zeros(size(t));
z_real = zeros(size(t));% 轨迹跟踪控制
for i = 2:length(t)% 误差计算ex = x_d(i) - x_real(i-1);ey = y_d(i) - y_real(i-1);ez = z_d(i) - z_real(i-1);% PID控制器u_x = Kp(1)*ex + Ki(1)*sum(ex) + Kd(1)*(ex - (x_real(i-1) - x_real(i-2)));u_y = Kp(2)*ey + Ki(2)*sum(ey) + Kd(2)*(ey - (y_real(i-1) - y_real(i-2)));u_z = Kp(3)*ez + Ki(3)*sum(ez) + Kd(3)*(ez - (z_real(i-1) - z_real(i-2)));% 更新实际轨迹x_real(i) = x_real(i-1) + u_x*0.1;y_real(i) = y_real(i-1) + u_y*0.1;z_real(i) = z_real(i-1) + u_z*0.1;
end% 绘制结果
figure;
subplot(3,1,1); plot(t, x_d, 'r', t, x_real, 'b'); title('X轴轨迹'); xlabel('时间/s'); ylabel('位置/m');
subplot(3,1,2); plot(t, y_d, 'r', t, y_real, 'b'); title('Y轴轨迹'); xlabel('时间/s'); ylabel('位置/m');
subplot(3,1,3); plot(t, z_d, 'r', t, z_real, 'b'); title('Z轴轨迹'); xlabel('时间/s'); ylabel('位置/m');
参考文献
❝
Khalil, H.K., Nonlinear Systems, 3rd Edition, Prentice Hall, 2002.
Slotine, J.J.E., and Li, W., Applied Nonlinear Control, Prentice-Hall, 1991.
Utkin, V.I., Sliding Modes in Control and Optimization, Springer-Verlag, 1992.
Huang, C.F., "Trajectory tracking control for a quadrotor UAV using integral backstepping approach," IEEE Transactions on Aerospace and Electronic Systems, vol. 45, no. 3, pp. 1065-1075, 2009.
(文章内容仅供参考,具体效果以图片为准)


















