一、活动参与地址
点击链接进行活动报名>>>https://momodel.cn/classroom/course/detail?id=6173911eab37f12b14daf4a8&activeKey=info&src=bef3adb478
二、活动详情
进入链接点击报名,仅需每天参与吴超老师的《人工智能导论》打卡活动,即可获得丰富奖励。
三、活动奖励
- 参与就送 20 次 ChatGPT 问答额度
- 日常打卡积分翻倍,积分可兑换课程、ChatGPT 额度、GPU 等
- 连续打卡 7 天送幸运现金红包
- 连续打卡14 天并完成 《人工智能导论》课程,送 1 个月 B 站大会员 or 价值 199.9 元《Python 极速入门特训营》课程
四、活动课程介绍
人人都能听得懂的 AI 入门指南来了! 快速掌握人工智能,只需20天!
《人工智能导论》-- 由**浙大教授吴超老师**精心打造!
- 20天8章节,AI入门不再难!
- 历史与未来:深入了解人工智能的过去、现在与未来。
- 核心概念:神经网络、过拟合、泛化能力,一网打尽。
- 实战应用:学习如何在不同场景下构建和应用AI模型。

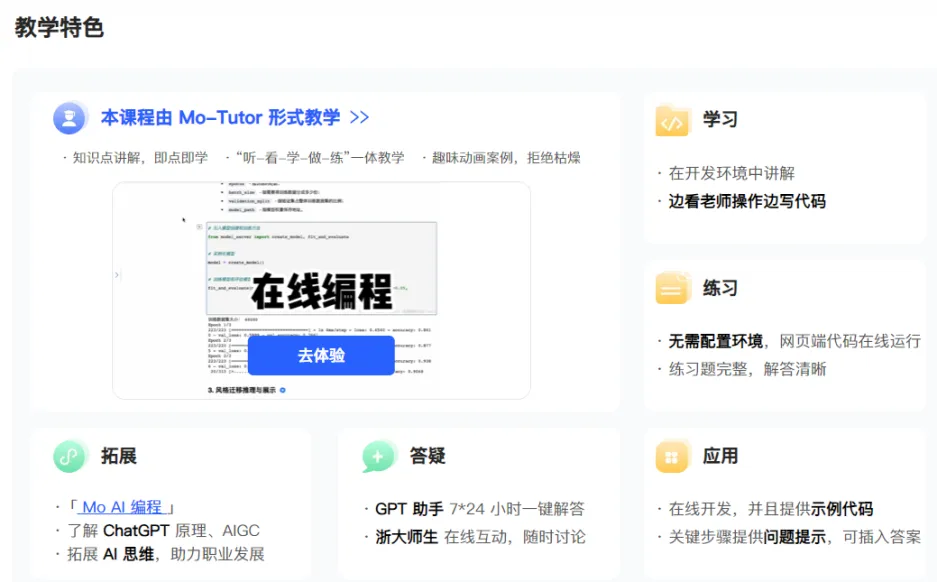
- Mo-Tutor模式,学习更高效!
- 全方位教学:听、看、学、做、练,一站式学习体验。
- 按需学习:哪里不懂点哪里,知识点讲解清晰明了。
- 生动案例:动画案例让你的学习不再枯燥。
- 代码实操:在线运行代码,学以致用,记忆更深刻。
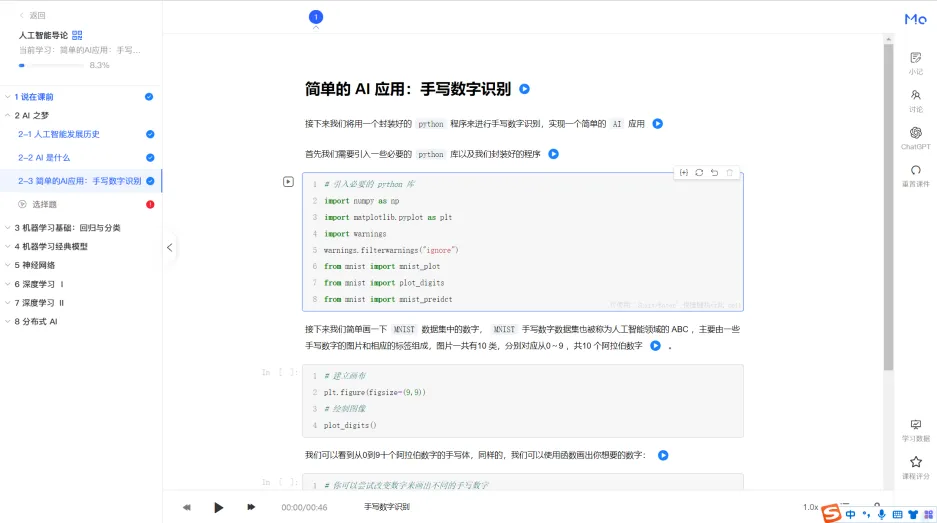
- 项目案例,让知识活起来!
- 实战演练:通过手写体识别、猫狗识别、风格迁移等项目案例,让你的AI知识更加扎实。
- 趣味性讲解:结合大量案例,让学习过程充满乐趣。

![[C++ 核心编程]笔记 4.1.4 类和对象 - 案例1](https://i-blog.csdnimg.cn/direct/6b627bfd3bb642438eade5852eadc648.png#pic_center)










![[论文阅读]SCOTT: Self-Consistent Chain-of-Thought Distillation](https://i-blog.csdnimg.cn/direct/0e038ca9152c4f94b575b5f23e118079.png)




