前言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

---

一、算法介绍

Q-Learning是一种基于值函数的强化学习算法，其目标是学习一个最优的行动价值函数（Q函数），从而指导智能体在不同状态下选择最优行动。Q-Learning属于离线策略学习方法，不依赖于策略的形式，因此具有较强的灵活性和普适性。

Q-Learning的基本概念：

• 状态（State, $s$）：环境在某一时刻的具体情况。
• 动作（Action, $a$）：智能体在某一状态下可以采取的行为。
• 奖励（Reward, $r$）：智能体执行动作后环境给予的反馈。
• 策略（Policy, $\pi$）：智能体选择动作的规则。
• Q函数（$Q(s,a)$）：在状态$s$下采取动作$a$所能获得的预期累积奖励。

Q-Learning通过不断更新Q函数，逐步逼近最优Q函数，从而找到最优策略。

二、算法原理

Q-Learning的核心在于更新Q函数，具体更新公式如下：

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha \left[r_{t+1}+\gamma \underset{a}{\max }Q(s_{t+1},a)-Q(s_t,a_t)\right]$$

其中：

• $s_t$：当前状态
• $a_t$：当前动作
• $r_{t+1}$：执行动作后获得的奖励
• $s_{t+1}$：下一个状态
• $\alpha$：学习率，控制新信息对Q值的影响程度
• $\gamma$：折扣因子，衡量未来奖励的重要性

算法步骤：

1. 初始化：为所有状态-动作对$(s,a)$初始化Q值，通常设为0。
2. 循环：
   • 在当前状态$s$下，选择一个动作$a$，通常采用$ϵ$-贪婪策略，以平衡探索与利用。
   • 执行动作$a$，观察奖励$r$和下一个状态$s^{\prime }$。
   • 更新Q值：
     $$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$
   • 将状态$s^{\prime }$设为新的当前状态$s$。
3. 终止：当达到终止条件（如达到最大迭代次数或收敛）时，算法结束。

三、案例分析：冰湖环境中的Q-Learning

3.1 环境描述

冰湖（Ice Lake）是一种模拟滑冰场景的强化学习环境，智能体需要在冰面上滑行，避开障碍物，最终到达目标位置。为了简化，本案例将冰湖环境抽象为一个二维网格，智能体需要通过选择合适的方向，将自身移动到目标位置。

3.2 环境设置

• 网格大小：$5\times 5$
• 起始位置：$(0,0)$
• 目标位置：$(4,4)$
• 障碍物：固定分布在网格中，智能体无法通过
• 动作空间：四个方向（上、下、左、右）
• 奖励机制：
  • 到达目标：$+10$
  • 每步移动：$-1$
  • 碰到障碍物：$-10$，并保持在原位置

3.3 部分代码

以下是使用Python实现的Q-Learning算法在冰湖环境中的部分代码。

# 主函数
if __name__ == "__main__":np.random.seed(0)random.seed(0)# 环境参数grid_size = 5env = IceLakeEnv(grid_size=grid_size)# Q-Learning参数epsilon = 0.5alpha = 0.1gamma = 0.9ncol = grid_sizenrow = grid_sizeagent = QLearning(ncol, nrow, epsilon, alpha, gamma)num_episodes = 100  # 训练回合数return_list = []  # 记录每一回合的回报# 训练过程for episode in tqdm(range(num_episodes), desc='Training Progress'):episode_return = 0state_tuple = env.reset()# 将状态元组转换为单一整数state = state_tuple[0] * grid_size + state_tuple[1]done = Falsewhile not done:action = agent.take_action(state)next_state_tuple, reward, done = env.step(action)next_state = next_state_tuple[0] * grid_size + next_state_tuple[1]agent.update(state, action, reward, next_state)episode_return += reward  # 累积回报state = next_statereturn_list.append(episode_return)# 绘制奖励函数曲线episodes_list = list(range(1, num_episodes + 1))plt.figure(figsize=(10, 6))plt.plot(episodes_list, return_list, marker='o')plt.xlabel('回合数 (Episodes)')plt.ylabel('累积奖励 (Returns)')plt.title('Q-Learning在冰湖环境中的奖励变化曲线')plt.grid(True)plt.show()# 打印最终的Q表和策略print("Q-learning算法最终收敛得到的策略为：")action_meaning = ['^', 'v', '<', '>']print_agent(agent, env, action_meaning)# 测试智能体并记录路径def test_agent(env, agent):state_tuple = env.reset()state = state_tuple[0] * env.grid_size + state_tuple[1]path = [state_tuple]done = Falsetotal_reward = 0while not done:action = np.argmax(agent.Q_table[state])next_state_tuple, reward, done = env.step(action)path.append(next_state_tuple)total_reward += rewardstate = next_state_tuple[0] * env.grid_size + next_state_tuple[1]return path, total_rewardpath, total_reward = test_agent(env, agent)print("路径:", path)print("总奖励:", total_reward)# 可视化环境布局和路径、策略print("环境布局及路径可视化:")env.render(path=path, policy=agent.Q_table)

3.4 运行结果

训练完成后，智能体应能逐步学习到从起始点到目标点的最优路径，并最大化累积奖励。输出结果如下：

Q-learning算法最终收敛得到的策略为：
> > v v v
v X > > v
v v X > v
> > v X v
> > > > G路径: [(0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (1, 4), (2, 4), (3, 4), (4, 4)]
总奖励: 3

奖励函数曲线如下：

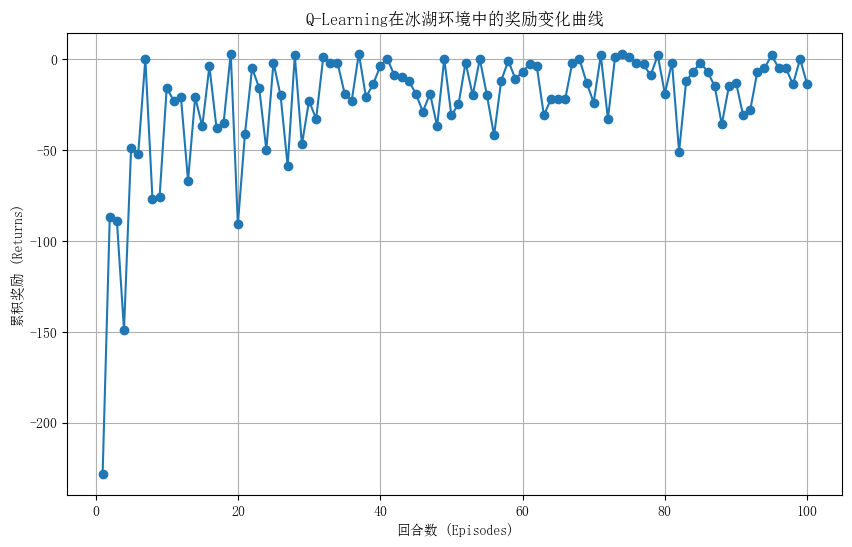
图中展示了Q-Learning算法在100个回合中的累积奖励变化。随着训练的进行，累积奖励逐渐增加，表明智能体的策略在不断优化，能够更快、更有效地到达目标位置，同时避开障碍物。

可视化最优路径如下：

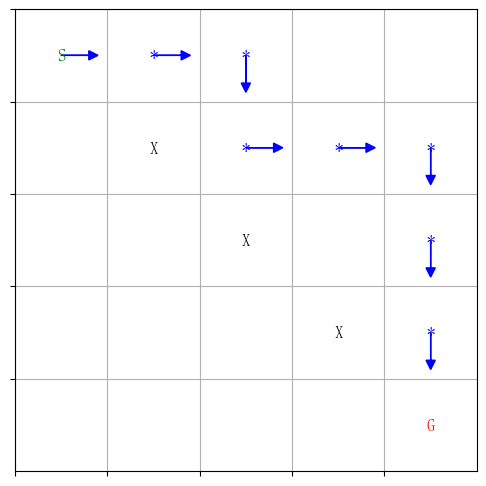
其中，S表示起点，G表示终点，X表示障碍物。

3.5 注意事项

• 障碍物位置：在本案例中，障碍物位置是固定的，以确保环境的稳定性，便于智能体学习最优策略。如果障碍物位置在每个回合中随机生成，可能会增加学习的难度，尤其是在回合数较少的情况下。

• 探索与利用的平衡：$ϵ$-贪婪策略中的$ϵ$值决定了智能体在探索新动作与利用已学知识之间的平衡。较高的$ϵ$促进探索，但可能导致收敛速度变慢；较低的$ϵ$则更倾向于利用，可能陷入局部最优。

• 学习率与折扣因子：学习率$\alpha$决定了新信息对Q值的影响程度；折扣因子$\gamma$衡量了未来奖励的重要性。两者的选择对算法的收敛性和最终策略有重要影响。

四、总结

Q-Learning作为一种经典的强化学习算法，通过学习状态-动作价值函数，实现了在各种环境中的策略优化。在冰湖环境的案例中，Q-Learning成功指导智能体找到最优路径，展示了其在策略决策中的有效性。通过引入障碍物和不同的奖励机制，进一步丰富了环境的复杂性，使算法在更具挑战性的情境中依然能够表现出色。

未来，可以进一步探索Q-Learning在更复杂环境中的应用，如多智能体协作、连续动作空间或动态环境变化等。此外，结合深度学习的方法（如深度Q网络，DQN）能够处理更大规模和高维度的问题，拓展Q-Learning的应用范围。