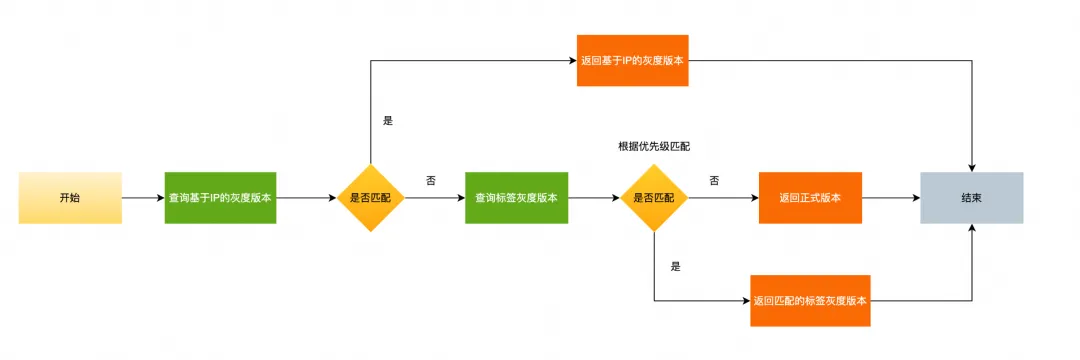
基于SVD的全秩矩阵逆
英文原文:
As you might remember from your undergraduate-level courses, every real matrix can be decomposed in its singular-value decomposition (SVD) as follows
A = U Σ V T A = U \Sigma V^T A=UΣVT
where U ∈ R m × m U \in \mathbb{R}^{m \times m} U∈Rm×mand V ∈ R n × n V \in \mathbb{R}^{n \times n} V∈Rn×n are orthonormal matrices (i.e., they are square, full rank, and their inverses are given by U U T = I m × m U U^T = I_{m \times m} UUT=Im×mand V V T = V T V = I n × n V V^T = V^T V = I_{n \times n} VVT=VTV=In×n). Moreover, Σ \Sigma Σ is a (rectangular) diagonal matrix composed of the singular values of the matrix given by σ i \sigma_i σifor i = 1 , … , m i = 1, \dots, m i=1,…,m, ordered from the largest singular value towards the smallest singular value. Note that singular values are always non-negative.
Note: All singular values of a given matrix will be non-zero when the matrix has full rank.
中文翻译:
如你在本科阶段课程中可能学到的那样,每个实矩阵都可以通过其奇异值分解 (SVD) 表示如下:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中, U ∈ R m × m U \in \mathbb{R}^{m \times m} U∈Rm×m 和 V ∈ R n × n V \in \mathbb{R}^{n \times n} V∈Rn×n是正交矩阵(即,它们是方阵,满秩,且它们的逆由 U U T = I m × m U U^T = I_{m \times m} UUT=Im×m和 V V T = V T V = I n × n V V^T = V^T V = I_{n \times n} VVT=VTV=In×n给出)。此外, Σ \Sigma Σ是一个(矩形的)对角矩阵,由矩阵的奇异值组成,记为 σ i \sigma_i σi , i = 1 , … , m i = 1, \dots, m i=1,…,m,按从最大奇异值到最小奇异值的顺序排列。请注意,奇异值总是非负的。
注意:当矩阵是满秩时,其所有奇异值都将是非零的。
解释
奇异值分解(SVD)是一种重要的矩阵分解方法,用于将一个矩阵分解为三个部分:一个正交矩阵 U U U、一个对角矩阵 Σ \Sigma Σ(包含矩阵的奇异值)和另一个正交矩阵 V V V。这种分解具有许多应用,如数据降维、矩阵逆计算和信号处理等。
-
正交矩阵 U U U 和 V V V:
- 正交矩阵的特点是它们的行和列是相互正交的(垂直的),且单位长度。
- 正交矩阵的逆等于它的转置,即 U U T = I U U^T = I UUT=I和 V V T = I V V^T = I VVT=I,这表明它们是满秩矩阵。
-
对角矩阵 Σ \Sigma Σ:
- Σ \Sigma Σ 包含了原矩阵的奇异值,这些奇异值是按从大到小的顺序排列的。
- 奇异值总是非负的,当矩阵是满秩时,所有奇异值都是非零的。
- 如果矩阵不是满秩,那么会有一些奇异值为零,这表示矩阵的某些行或列之间存在线性依赖。
-
满秩矩阵的性质:
- 如果矩阵是满秩的,那么它的所有奇异值都是非零的。
- 满秩意味着矩阵的行或列是线性独立的,能够代表完整的信息。
这种奇异值分解可以帮助我们分析矩阵的结构,特别是在矩阵可能是奇异或非方形的情况下,SVD 提供了计算伪逆和解决不适定问题的一种方法。
右伪逆
英文原文:
With these properties, a right pseudo-inverse can be defined for any matrix for which all singular values are non-zero. The right pseudo-inverse is
A † ≜ V Σ inv U T . A^\dagger \triangleq V \Sigma^{\text{inv}} U^T. A†≜VΣinvUT.
where Σ inv \Sigma^{\text{inv} } Σinv is a compatible matrix where we use the reciprocal of the singular values. For example, for a square matrix we have
Σ inv ≜ [ 1 σ 1 0 ⋯ 0 0 1 σ 2 ⋯ 0 0 0 ⋱ 0 0 0 0 1 σ m ] \Sigma^{\text{inv}} \triangleq \begin{bmatrix} \frac{1}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{\sigma_2} & \cdots & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \frac{1}{\sigma_m} \end{bmatrix} Σinv≜ σ110000σ2100⋯⋯⋱0000σm1
and for a rectangular matrix
Σ inv ≜ [ 1 σ 1 0 ⋯ 0 0 1 σ 2 ⋯ 0 0 0 ⋱ 0 0 0 0 1 σ m 0 0 0 0 ] \Sigma^{\text{inv}} \triangleq \begin{bmatrix} \frac{1}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{\sigma_2} & \cdots & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \frac{1}{\sigma_m} \\ 0 & 0 & 0 & 0 \end{bmatrix} Σinv≜ σ1100000σ21000⋯⋯⋱00000σm10
中文翻译:
基于这些性质,可以为所有奇异值均非零的矩阵定义右伪逆。右伪逆定义为:
A † ≜ V Σ inv U T . A^\dagger \triangleq V \Sigma^{\text{inv}} U^T. A†≜VΣinvUT.
其中, Σ inv \Sigma^{\text{inv} } Σinv 是一个与 Σ \Sigma Σ 兼容的矩阵,其中每个奇异值取倒数。
例如,对于方阵,我们有
Σ inv ≜ [ 1 σ 1 0 ⋯ 0 0 1 σ 2 ⋯ 0 0 0 ⋱ 0 0 0 0 1 σ m ] \Sigma^{\text{inv}} \triangleq \begin{bmatrix} \frac{1}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{\sigma_2} & \cdots & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \frac{1}{\sigma_m} \end{bmatrix} Σinv≜ σ110000σ2100⋯⋯⋱0000σm1
对于矩形矩阵
Σ inv ≜ [ 1 σ 1 0 ⋯ 0 0 1 σ 2 ⋯ 0 0 0 ⋱ 0 0 0 0 1 σ m 0 0 0 0 ] \Sigma^{\text{inv}} \triangleq \begin{bmatrix} \frac{1}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{\sigma_2} & \cdots & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \frac{1}{\sigma_m} \\ 0 & 0 & 0 & 0 \end{bmatrix} Σinv≜ σ1100000σ21000⋯⋯⋱00000σm10
解释
这段文字解释了如何利用奇异值分解(SVD)来构造矩阵的伪逆(pseudo-inverse)。伪逆是一种“广义逆”,特别适用于非方阵和奇异矩阵的情况,即矩阵可能没有标准的逆。
-
伪逆的构造方法:
- 给定一个矩阵 A A A,我们可以将其分解为 A = U Σ V T A = U \Sigma V^T A=UΣVT。
- 要构造 A A A 的伪逆 A † A^\dagger A†,我们需要使用 V V V、 Σ inv \Sigma^{\text{inv}} Σinv 和 U T U^T UT。
- 这里, Σ inv \Sigma^{\text{inv}} Σinv 是对角矩阵 Σ \Sigma Σ 的“逆”,其中包含 Σ \Sigma Σ 中奇异值的倒数。
-
对角矩阵 Σ inv \Sigma^{\text{inv}} Σinv:
- 如果 Σ \Sigma Σ 中的奇异值是 σ 1 , σ 2 , … , σ m \sigma_1, \sigma_2, \dots, \sigma_m σ1,σ2,…,σm,那么 Σ inv \Sigma^{\text{inv}} Σinv 的对角线上将是它们的倒数 1 σ 1 , 1 σ 2 , … , 1 σ m \frac{1}{\sigma_1}, \frac{1}{\sigma_2}, \dots, \frac{1}{\sigma_m} σ11,σ21,…,σm1。
- 这要求所有奇异值 σ i \sigma_i σi 非零,否则无法取倒数。因此,仅当矩阵满秩时,才可以直接使用这种方式计算伪逆。
总之,右伪逆是通过SVD构造的一种广义逆矩阵,对于矩阵奇异值均为非零的满秩矩阵,它是存在且唯一的。
当矩阵为矩形时如何构造其伪逆的对角矩阵 Σ inv \Sigma^{\text{inv}} Σinv。
-
矩形矩阵的奇异值分解:
- 对于一个矩形矩阵 A A A,奇异值分解 (SVD) 仍然适用,可以将其分解为 A = U Σ V T A = U \Sigma V^T A=UΣVT。
- 其中 Σ \Sigma Σ 是一个对角矩阵,但它的大小可能并不是方阵,而是一个矩形(例如 m × n m \times n m×n)。
-
伪逆矩阵 Σ inv \Sigma^{\text{inv}} Σinv 的构造:
- 当 A A A 是矩形时, Σ inv \Sigma^{\text{inv}} Σinv的构造略有不同。
- 对于所有非零的奇异值 σ i \sigma_i σi,我们在对角线上填入其倒数 1 σ i \frac{1}{\sigma_i} σi1。
- 如果 A A A是 m × n m \times n m×n 的矩阵,并且 m ≠ n m \neq n m=n,则 Σ inv \Sigma^{\text{inv}} Σinv的大小将与 Σ \Sigma Σ兼容,但可能在矩阵的末尾出现额外的零行或零列。
-
作用:
- 通过将 Σ \Sigma Σ 中的奇异值取倒数填入 Σ inv \Sigma^{\text{inv}} Σinv 中,我们可以构造矩形矩阵的伪逆 A † = V Σ inv U T A^\dagger = V \Sigma^{\text{inv}} U^T A†=VΣinvUT。
- 这种伪逆在最小二乘解、数据降维等领域有广泛应用,特别是在原矩阵没有标准逆的情况下。
总结来说,这种方法可以让我们在矩形矩阵上应用伪逆,即使矩阵不满秩或不为方阵,这在实际计算中具有重要意义。