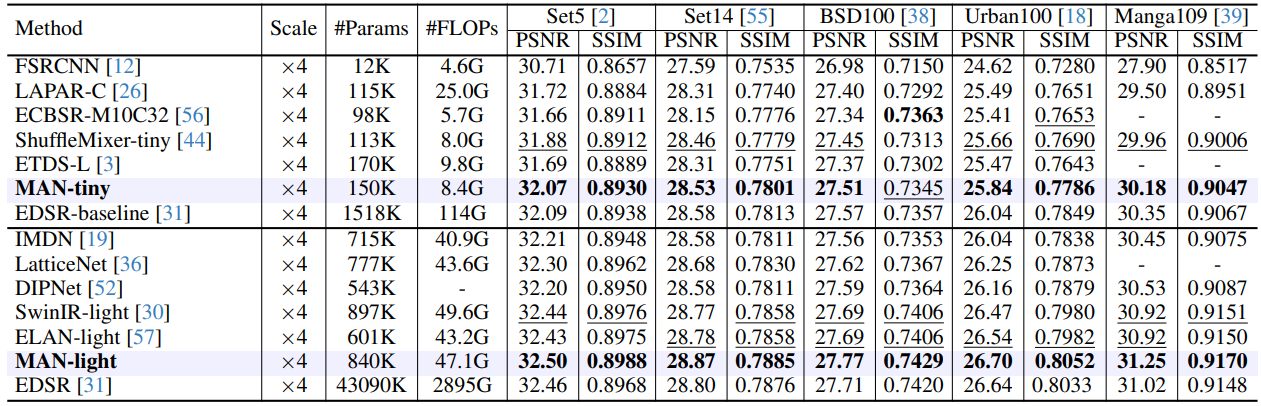
SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers
一、前言
扩散模型为代表的生成式模型,以其深刻的还原论的哲学原理作为内在基础,辅以机器学习领域各类优秀的模型设计,在各个学术和应用领域都有着惊艳的表现。近期,基于 Transformer 架构的扩散模型在图像和视频生成领域在更大的模型和数据集中取得的成功引起了社会各界的关注。本文基于论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》,归纳扩散模型的技术演进,包括理论框架、训练方式、网络设计、采样方式等方面的新进展,分析各项背后的数学原理,总结相关经验。
二、扩散模型简介
为了在本文中统一以扩散模型为代表的基于概率流的生成模型(Probabilistic flow based generative model)的变量、函数、参数的记法,将进行一些简单概念的定义与介绍。
(一)扩散过程的定义
对于分布为 x d a t a p ( x d a t a ) x_{data}~p(x_{data}) xdata p(xdata) 的原数据,建立一个扩散模型 p θ ( x ) p_\theta (x) pθ(x) 来重建该分布。具体的,它通过对原数据分布 p ( x d a t a ) p(x_{data}) p(xdata) 在一个扩散过程中的各个时刻的变化态势进行还原,从而回溯重建原有的数据分布。
扩散过程会让数据的分布逐渐趋于一个高斯分布:
lim t ↑ x t → N ( x t ; 0 , Σ I ) \lim_{t \uparrow} x_t \to \mathcal{N}(x_t; 0, \Sigma I) t↑limxt→N(xt;0,ΣI)
假设扩散过程的时长区间为 [ 0 , T ] [0, T] [0,T] 的扩散过程的任意时间刻的状态可以被表示为:
x t : = α t x d a t a + σ t ϵ x_t := \alpha_t x_{data} + \sigma_t \epsilon xt:=αtxdata+σtϵ
其中, α t \alpha_t αt 为扩散过程中原数据保留的幅值系数(Scale),它随着 t t t 单调减小;为扩散过程中引入的高斯噪声的幅值,它随着 t t t 单调增大。此外,也可以使用一个随机微分方程来描述扩散过程中的变化量:
d x t = f ( x t , t ) d t + g ( t ) d w t dx_t = f(x_t, t)dt + g(t)dw_t dxt=f(xt,t)dt+g(t)dwt
式中, w t w_t wt 是 Wiener 过程(也称为标准布朗运动(Standard Brownian Motion)), f ( x t , t ) f(x_t, t) f(xt,t) 为某种形式的漂移项, g ( t ) g(t) g(t) 为扩散过程的扩散系数。因此,定义一个扩散过程,等价于定义 α t \alpha_t αt 与 σ t \sigma_t σt,或是等价于定义 f ( x t , t ) f(x_t, t) f(xt,t) 与 g ( t ) g(t) g(t) 的数学形式。
(二)扩散模型的建模
根据 Fokker–Planck equation,存在一个由以下常微分方程描述的过程,与该扩散过程具有相同的概率密度分布:
d x t = ( f ( x t , t ) − g 2 ( t ) 2 ∇ x t log p ( x t , t ) ) d t dx_t = \left( f(x_t, t) - \frac{g^2(t)}{2} \nabla_{x_t} \log p(x_t, t) \right) dt dxt=(f(xt,t)−2g2(t)∇xtlogp(xt,t))dt
因此还原该扩散过程等价于建立关于扩散过程中各个时刻状态变化的模型,比如建立得分函数的模型(Score function model), s θ ( x t ) s_\theta(x_t) sθ(xt):
s θ ( x t ) : = ∇ x t log p ( x t , t ) s_\theta(x_t) := \nabla_{x_t} \log p(x_t, t) sθ(xt):=∇xtlogp(xt,t)
或是建立常微分方程的流场的速度, v θ ( x t , t ) \mathbf{v_\theta}(x_t, t) vθ(xt,t),作为控制生成的速度模型(Velocity model):
v θ ( x t , t ) = f ( x t , t ) − g 2 ( t ) 2 ∇ x t log p ( x t , t ) \mathbf{v_\theta}(x_t, t) = f(x_t, t) - \frac{g^2(t)}{2} \nabla_{x_t} \log p(x_t, t) vθ(xt,t)=f(xt,t)−2g2(t)∇xtlogp(xt,t)
(三)扩散模型的采样
为了生成数据,在采样的过程中,可以通过逆向求解上述常微分方程,来逐步还原原有数据的分布:
d x t = ( f ( x t , t ) − g 2 ( t ) 2 s θ ( x t , t ) ) d t dx_t = \left( f(x_t, t) - \frac{g^2(t)}{2} s_\theta(x_t, t) \right) dt dxt=(f(xt,t)−2g2(t)sθ(xt,t))dt
d x t = v θ ( x t , t ) d t dx_t = \mathbf{v_\theta}(x_t, t) dt dxt=vθ(xt,t)dt
也可以通过逆向求解与上述常微分方程同概率分布的随机微分方程,来逐步还原原有数据的分布:
d x t = ( f ( x t , t ) − ( g 2 ( t ) 2 + g w 2 ( t ) 2 ) s θ ( x t , t ) ) d t + g w ( t ) d w ˉ t dx_t = \left( f(x_t, t) - (\frac{g^2(t)}{2} + \frac{g_w^2(t)}{2}) s_\theta(x_t, t) \right)dt + g_w(t) d\bar{w}_t dxt=(f(xt,t)−(2g2(t)+2gw2(t))sθ(xt,t))dt+gw(t)dwˉt
d x t = ( v θ ( x t , t ) − g w 2 ( t ) 2 s θ ( x t , t ) ) d t + g w ( t ) d w ˉ t dx_t = \left( \mathbf{v_\theta}(x_t, t) - \frac{g_w^2(t)}{2} s_\theta(x_t, t) \right) dt + g_w(t) d\bar{w}_t dxt=(vθ(xt,t)−2gw2(t)sθ(xt,t))dt+gw(t)dwˉt
式中, w ˉ t \bar{w}_t wˉt 是逆向时间的 Wiener 过程, g w ( t ) g_w(t) gw(t) 是逆过程中引入的某种自定义的扩散系数。
三、技术演进
总的来说,扩散模型的技术进步由以下几个独立的维度构成。
(一)时间形式:从离散时间到连续时间建模
早期的扩散模型,比如 DDPM、NCSN 等,使用了一种离散的时间形式来记录扩散过程,即 t ∈ [ 0 , T ] t \in [0, T] t∈[0,T] 是一个整数,作为每一个求解的阶段的索引:
q ( x i ∣ x i + 1 ) = N ( μ ~ i , β ~ i I ) q(x_i | x_{i+1}) = \mathcal{N}(\tilde{\mu}_i, \tilde{\beta}_i I) q(xi∣xi+1)=N(μ~i,β~iI)
论文《Score-Based Generative Modeling through Stochastic Differential Equations》最早统一了离散时间和连续时间扩散模型的数学形式之间的内在联系。在连续时间的扩散过程中,一般会将扩散过程的时长区间设定为 [ 0 , 1 ] [0, 1] [0,1],而论文《Elucidating the Design Space of Diffusion-Based Generative Models》的工作展示了扩散模型的时间区间的数学含义,它本质上是扩散后噪声幅值的重参数化。因此,对于扩散模型而言,时间 t t t 即噪音 σ t \sigma_t σt。
由于扩散过程的 σ t \sigma_t σt 本质上是连续的,这要求模型在各个噪音幅值下都能习得重建数据的方案,因此,需要在连续的时间中优化扩散模型,以及在连续的时间中采样生成。在训练过程中,连续的时间建模可以让扩散模型的训练更稳定,因为损失函数可以更加均匀地平滑地访问时间区间 t ∈ [ 0 , 1 ] t \in [0, 1] t∈[0,1]。而在生成过程中,连续的时间建模可以允许不再将求解过程使用常微分方程的数值解算器,可适应地调整步长生成,访问各个时间刻的扩散模型,而非只能使用设定的离散的步长。
论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》的基线实验结果也表明,连续的时间建模取得了更好的性能表现。

(二)扩散过程:从方差守恒扩散过程到广义扩散过程
根据扩散过程的定义,
x t ∣ x d a t a : = α t x d a t a + σ t ϵ , x_t \mid x_{data} := \alpha_t x_{data} + \sigma_t \epsilon, xt∣xdata:=αtxdata+σtϵ,
可知, α t \alpha_t αt 与 σ t \sigma_t σt 的数学形式决定了扩散过程的类型。
论文《Elucidating the Design Space of Diffusion-Based Generative Models》的工作最早统一了不同类型的扩散过程的数学形式。它揭示了所有类型的扩散过程都是同一个扩散模型,
d x = 2 t d w t dx = \sqrt{2t}dw_t dx=2tdwt
在时间上的重参数化, σ : = t ⟶ σ : = σ ( t ) \sigma := t \longrightarrow \sigma := \sigma(t) σ:=t⟶σ:=σ(t),以及在数值上的缩放, x t ⟶ x t s ( t ) x_t \longrightarrow \frac{x_t}{s(t)} xt⟶s(t)xt:
d x t = s ′ ( t ) s ( t ) x t d t + s ( t ) 2 σ t ′ σ t d w t dx_t = \frac{s'(t)}{s(t)} x_t dt + s(t) \sqrt{2\sigma'_t \sigma_t} dw_t dxt=s(t)s′(t)xtdt+s(t)2σt′σtdwt
虽然可以认为,不同类型的扩散模型本质上都是同一个过程,并不存在绝对数学意义上的优化之分,但不同的参数化形式还是会在实验室上影响训练的稳定性和生成的质量。
早期的扩散模型,比如 DDPM,或是其连续时间形式,VP-SDE,是一种方差守恒(Variance-Preserving, VP)的扩散过程,它使用了如下参数化形式的 α t \alpha_t αt 与 σ t \sigma_t σt:
α t = e − 1 2 ∫ 0 t β ( s ) d s \alpha_t = e^{-\frac{1}{2} \int_0^t \beta(s)ds} αt=e−21∫0tβ(s)ds
σ t = 1 − e − ∫ 0 t β ( s ) d s \sigma_t = \sqrt{1 - e^{-\int_0^t \beta(s)ds}} σt=1−e−∫0tβ(s)ds
默认数据正则化后, V [ x 0 ] = 1 \mathbb{V}[x_0] = 1 V[x0]=1,因此扩散过程中的方差守恒,即 V [ x t ] = α t 2 V [ x 0 ] + σ t 2 = 1 \mathbb{V}[x_t] = \alpha_t^2 \mathbb{V}[x_0] + \sigma_t^2 = 1 V[xt]=αt2V[x0]+σt2=1。
通过更自由地定义 α t \alpha_t αt 与 σ t \sigma_t σt,可以获得更多形式灵活的随机插值器(Stochastic interpolants)作为扩散过程,只需要保证 α t \alpha_t αt 与 σ t \sigma_t σt 是连续可微分的,且保证 α 1 = σ 0 = 0 \alpha_1 = \sigma_0 = 0 α1=σ0=0,即 σ 1 = α 0 = 0 \sigma_1 = \alpha_0 = 0 σ1=α0=0 即可。
比如在论文《Elucidating the Design Space of Diffusion-Based Generative Models》中,使用了线性的扩散过程:
α t = 1 − t \alpha_t = 1 - t αt=1−t
σ t = t \sigma_t = t σt=t
或是利用三角函数的数学性质改进方差守恒扩散过程,让其形式更加自然,称之为广义方差守恒扩散过程(Generalized VP-SDE, GVP):
α t = cos ( 1 2 π t ) \alpha_t = \cos\left(\frac{1}{2} \pi t\right) αt=cos(21πt)
σ t = sin ( 1 2 π t ) \sigma_t = \sin\left(\frac{1}{2} \pi t\right) σt=sin(21πt)

论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》中的实验表明,如上图所示,线性的扩散过程(Linear)或广义方差守恒扩散过程(GVP)比 VP-SDE 有更小的流线长度(Path length),这意味着前两者的生成路径更平滑更直,速度场的变化量更小,模型的建模会更容易,采样时求解器的数值误差也会更小,在标准数据集上也有显著更好的表现。
这或许是因为,一般对于图片数据,建模的维度越高,模型容量会越大,但数据量受限于采集成本,并不会增加太多,因此模型容量相比数据量很充足,数据的生成路径会很稀疏,此时更平滑更直的生成路径在建模上更有优势。
当然,也存在这样的学术观点:并不是生成路径更平滑更直,模型表现一定会越好,或许对于某些数据集和应用场景,弯曲的生成路径也是有意义的,比如它可能在同参数下有更大的模型容量,从而建模更为丰富的数据对象。此外,也并不是所有的弯曲的生成路径都有意义,比如生成路径中假如存在回旋的涡流,那么显然这样的弯曲路径对于路径末端的生成结果是没有意义的。
(三)训练方式:从得分函数匹配到流匹配
除了扩散过程的数学形式之外,扩散模型的表现也会受到其训练方式的影响,具体来说,包括建模方式和模型训练目标。
1. 建模方式
扩散模型有多种建模方式,比如建模得分函数(Score function model), s θ ( x t , t ) s_\theta(x_t, t) sθ(xt,t):
s θ ( x t , t ) : = ∇ x t log p ( x t , t ) s_\theta(x_t, t) := \nabla_{x_t} \log p(x_t, t) sθ(xt,t):=∇xtlogp(xt,t)
或是建模噪音函数(noise function model), ϵ θ ( x t , t ) \epsilon_\theta(x_t, t) ϵθ(xt,t),它的数值大小近似于高斯噪音 ϵ \epsilon ϵ:
ϵ θ ( x t , t ) : = − σ t ∇ x t log p ( x t , t ) \epsilon_\theta(x_t, t) := -\sigma_t \nabla_{x_t} \log p(x_t, t) ϵθ(xt,t):=−σt∇xtlogp(xt,t)
或是建模流场的速度模型(Velocity model), v θ ( x t , t ) \mathbf{v_\theta}(x_t, t) vθ(xt,t):
v θ ( x t , t ) : = f ( x t , t ) − g 2 ( t ) 2 ∇ x t log p ( x t , t ) \mathbf{v_\theta}(x_t, t) := f(x_t, t) - \frac{g^2(t)}{2} \nabla_{x_t} \log p(x_t, t) vθ(xt,t):=f(xt,t)−2g2(t)∇xtlogp(xt,t)
或是比如在论文《Elucidating the Design Space of Diffusion-Based Generative Models》中,使用了降噪器模型(Denoiser function model), D θ ( x t , σ t ) D_\theta(x_t, \sigma_t) Dθ(xt,σt),它的数值大小近似于扩散过程中的 x t x_t xt:
D θ ( x t s ( t ) , σ t ) : = σ t 2 ∇ x t log p ( x t ) + x t s ( t ) D_\theta(\frac{x_t}{s(t)}, \sigma_t) := \sigma_t^2 \nabla_{x_t} \log p(x_t) + \frac{x_t}{s(t)} Dθ(s(t)xt,σt):=σt2∇xtlogp(xt)+s(t)xt
当定义好一种扩散过程之后,它们之间存在着确定性的数学转换关系。因此,不同的建模类型没有数学本质上的差异,但会在神经网络的建模数值稳定性和拟合精度上产生差别,毕竟任何神经网络的拟合能力都是有限的。
比如对于 VE-SDE 模型,在 t → 0 t \rightarrow 0 t→0 时, s θ ( x t ) s_\theta(x_t) sθ(xt) 会趋向于极值,而在其它 t t t 范围内, s θ ( x t ) s_\theta(x_t) sθ(xt) 会是某个有限的值。因此,网络可能需要建模一个较大的数值范围,因而需要特殊的设计来稳定训练过程。
不过理想情况下,假如模型作为拟合器是完美的或近乎完美的,那么建模方式对扩散模型的表现影响并不大。论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》中的实验结果也佐证了这一点。

2. 训练目标
相对于建模方式,扩散模型训练目标对最终表现的影响会更大一些。具体来说,扩散模型有两种训练目标。第一种是得分函数匹配(Score Matching),它尝试拟合扩散过程的得分函数, ∇ x t log p ( x t ) \nabla_{x_t} \log p(x_t) ∇xtlogp(xt),即概率分布密度的对数的梯度:
L s ( θ ) = E t , x t [ ∥ s θ ( x t ) − ∇ x t log p ( x t ) ∥ 2 ] L_s(\theta) = \mathbb{E}_{t, x_t} \left[ \| s_\theta(x_t) - \nabla_{x_t} \log p(x_t) \|^2 \right] Ls(θ)=Et,xt[∥sθ(xt)−∇xtlogp(xt)∥2]
论文《A connection between score matching and denoising autoencoders》的理论推导论证了,可以使用条件生成的数值解析的得分函数, ∇ x t log p ( x t ∣ x 0 ) \nabla_{x_t} \log p(x_t \mid x_0) ∇xtlogp(xt∣x0),来训练全局样本的得分函数, ∇ x t log p ( x t ) \nabla_{x_t} \log p(x_t) ∇xtlogp(xt):
L s ( θ ) = E t , x 0 , x t [ ∥ s θ ( x t ) − ∇ x t log p ( x t ∣ x 0 ) ∥ 2 ] + Const L_s(\theta) = \mathbb{E}_{t, x_0, x_t} \left[ \| s_\theta(x_t) - \nabla_{x_t} \log p(x_t \mid x_0) \|^2 \right] + \text{Const} Ls(θ)=Et,x0,xt[∥sθ(xt)−∇xtlogp(xt∣x0)∥2]+Const
为了训练目标的数值稳定,会添加权重 λ ( t ) \lambda(t) λ(t) 以稳定得分函数匹配的训练目标:
L s ( θ ) = E t [ λ ( t ) E x 0 , x t ∥ s θ ( x t ) − ∇ x t log p ( x t ∣ x 0 ) ∥ 2 ] L_s(\theta) = \mathbb{E}_{t} \left[ \lambda(t) \mathbb{E}_{x_0, x_t} \| s_\theta(x_t) - \nabla_{x_t} \log p(x_t \mid x_0) \|^2 \right] Ls(θ)=Et[λ(t)Ex0,xt∥sθ(xt)−∇xtlogp(xt∣x0)∥2]
一般使用 σ t \sigma_t σt 作为训练时的权重 λ ( t ) \lambda(t) λ(t),从而让数值稳定在高斯噪音 ϵ \epsilon ϵ 的数值大小附近,有如下形式:
L s ( θ ) = E t , x 0 , x t [ ∥ σ t s θ ( x t ) − σ t ∇ x t log p ( x t ∣ x 0 ) ∥ 2 ] = E t , x 0 , x t [ ∥ ϵ θ ( x t , t ) − ϵ ∥ 2 ] L_s(\theta) = \mathbb{E}_{t, x_0, x_t} \left[ \| \sigma_t s_\theta(x_t) - \sigma_t \nabla_{x_t} \log p(x_t \mid x_0) \|^2 \right] = \mathbb{E}_{t, x_0, x_t} \left[ \| \epsilon_\theta(x_t,t) - \epsilon \|^2 \right] Ls(θ)=Et,x0,xt[∥σtsθ(xt)−σt∇xtlogp(xt∣x0)∥2]=Et,x0,xt[∥ϵθ(xt,t)−ϵ∥2]
另一种训练目标称为流匹配(Flow Matching),它尝试拟合流模型的速度场:
L v ( θ ) = E t [ E x t [ ∥ v θ ( x t , t ) − v ( x t , t ) ∥ 2 ] ] L_v(\theta) = \mathbb{E}_{t} \left[ \mathbb{E}_{x_t} \left[ \| v_\theta(x_t, t) - v(x_t, t) \|^2 \right] \right] Lv(θ)=Et[Ext[∥vθ(xt,t)−v(xt,t)∥2]]
具体的,在扩散模型等概率流模型中,该流场任意位置的平均速度是概率密度加权的平均速度,即遵循流场的动量守恒:
v ( x t , t ) : = E x t [ d x t d t ] = E x t , x 0 [ v ( x t , t ∣ x 0 ) ] v(x_t, t) := \mathbb{E}_{ x_t} \left[ \frac{dx_t}{dt} \right] = \mathbb{E}_{x_t, x_0} \left[ v(x_t, t | x_0)\right] v(xt,t):=Ext[dtdxt]=Ext,x0[v(xt,t∣x0)]
p ( x t ) v ( x t , t ) = ∫ x 0 p ( x t ∣ x 0 ) p ( x 0 ) v ( x t , t ∣ x 0 ) d x 0 p(x_t) v(x_t, t) = \int_{x_0} p(x_t \mid x_0) p(x_0) v(x_t, t \mid x_0) dx_0 p(xt)v(xt,t)=∫x0p(xt∣x0)p(x0)v(xt,t∣x0)dx0
论文《Flow Matching for Generative Modeling》[10] 的理论推导论证了,可以使用条件生成的可数值解析的流速, v ( x t , t ∣ x 0 ) v(x_t, t \mid x_0) v(xt,t∣x0),来训练全局样本的速度场:
L v ( θ ) = E t E x t , x 0 [ ∥ v θ ( x t , t ) − v ( x t , t ∣ x 0 ) ∥ 2 ] + Const L_v(\theta) = \mathbb{E}_{t} \mathbb{E}_{x_t, x_0} \left[ \| v_\theta(x_t, t) - v(x_t, t \mid x_0) \|^2 \right] + \text{Const} Lv(θ)=EtExt,x0[∥vθ(xt,t)−v(xt,t∣x0)∥2]+Const
论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》论文得分函数匹配和流匹配之间存在互相加权的等价关系,因此即便使用了得分函数建模扩散模型,也可以使用流匹配的方法进行模型训练:
L v ( θ ) = E t [ ( σ t ′ − α t ′ σ t α t ) 2 E x 0 , x t [ ∥ σ t s θ ( x t , t ) − σ t ∇ x t log p ( x t ∣ x 0 ) ∥ 2 ] ] L_v(\theta) = \mathbb{E}_t \left[ \left( {\sigma'_t} - \frac{\alpha'_t \sigma_t}{\alpha_t} \right)^2 \mathbb{E}_{x_0, x_t} \left[ \| \sigma_t s_\theta(x_t, t) - \sigma_t \nabla_{x_t} \log p(x_t \mid x_0) \|^2 \right] \right] Lv(θ)=Et[(σt′−αtαt′σt)2Ex0,xt[∥σtsθ(xt,t)−σt∇xtlogp(xt∣x0)∥2]]
从论文中的基线实验来看,使用流匹配方法训练的模型取得了显著更好的成绩。这或许是因为后者的数学本质更为直观,因而它的权重是合乎自然更合理的。而得分函数匹配的权重是为了保证模型的数值稳定而人为设计的,可能并不是最优的参数。
(四)网络设计:从 U-Net 网络到 Transformer 网络
网络设计对扩散模型的表现至关重要。扩散模型的神经网络需要处理三个变量,当前状态变量 x t x_t xt,当前时间变量 t t t 与条件变量 c c c。
其中,条件变量 c c c 的处理与它的数据类型有关。比如对于文本类条件变量,会使用各类文本编码器的神经网络处理它。在论文《GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models》中用于文本生成图像的扩散模型使用了 Transformer 网络。或是比如条件变量 c c c 与状态变量 x t x_t xt 的性质类似,则可能会将其与状态变量 x t x_t xt 使用类似的网络进行处理。因此,关于条件变量 c c c,本文不做深入探讨。
处理时间变量 t t t 的网络会使用不同频率三角函数在时间变量 t t t 时的数值作为输出,将其映射成为模型内在的编码变量(embedding),这样时间变量 t t t 就可以感应激活不同频率的信号,作为下游的模型主干的输入。
由于扩散模型常被用于建模图像数据,因此状态变量 x t x_t xt 在早期的工作中往往使用基于卷积神经网络、残差网络,以及注意力层(Attention Layer)的 U-Net 网络。而在模型较低维度的数据时,状态变量 x t x_t xt 需要使用多层感知器和残差网络结构的 U-Net 网络结构即可。

具体的,在论文《Denoising Diffusion Probabilistic Models》,《Diffusion Models Beat GANs on Image Synthesis》和《High-Resolution Image Synthesis with Latent Diffusion Models》的扩散模型的U-Net网络中,在中间块(Middle block),下采样块(Down sampling block)和上采样块(Up sampling block)中使用了多层的残差网络块与注意力层。
以 Stable Diffusion V1 版本的开源代码 [16] 为例,U-Net 网络的每一级串联了两层残差卷积神经网络和一层残差注意力层网络,前者使用了 Swish 函数作为非线性激活函数,使用了 Group Norm 作为归一化模块。
近期,基于 Vision Transformer (ViT) 架构的网络在图像领域得到了广泛的应用。Transformer 网络将状态变量 x t x_t xt 分割为带有位置信息编码(Position Embedding)的序列,并多层串联使用带有残差网络的自注意力层(Self-Attention Layer)和多层感知器,实现对状态变量 x t x_t xt 的处理。
在监督类任务上,Vision Transformer 已经表现出比 U-Net 网络更好的在增大模型和数据集规模上的性能优势。因此,一些研究开始关注是否在生成类任务上,Vision Transformer 架构也能有这样的表现。论文《Scalable Diffusion Models with Transformers》的结果表明,将 Vision Transformer 网络架构用于扩散模型的主干网络的建模,确实让它更好地适配更大规模的模型训练。

在论文《Scalable Diffusion Models with Transformers》对 Transformer 网络的设计细节进行了多种类型的尝试,发现使用 FILM 架构设计来融合条件信息,利用可适应的层归一化块(Adaptive layer norm block, adaLN)替代原有的归一化块,并将每个残差网络初始化为一个恒等函数(identity function)有着最好的模型表现。具体的,需要将每一个残差网络中最后一层的幅值网络(scale)初始化为零,即图中的 α = 0 \alpha = 0 α=0。此外,将残差网络中第一层幅值网络初始化为一,偏置网络初始化为零,即 β = 1 \beta = 1 β=1 且 γ = 0 \gamma = 0 γ=0,也会有利于模型的训练。
对比两种架构设计,可以看到在Transformer网络中,全局的卷积和信息提取发生在初始的编码空间维度中。并且受益于残差网络的恒等映射的性质,增大Transformer网络的深度并不会过多增加训练模型的难度,因为总是可以等价地将其中若干层网络处理为恒等映射从而屏蔽它们,因此增大Transformer网络的深度会有利于建模更大的数据集。而对于U-Net网络,虽然它也有注意力层,(或许从某种意义上说,也可以将使用了注意力层的U-Net网络的浅层网络视为某种特殊形式Transformer 网络)但受限于U-Net网络的设计理念,其中注意力层的参数设计较为简易,浅层网络的层数也较小,导致浅层模型容量有限。而对于 U-Net 网络的深层网络,由于信息的深入压缩,深层网络中编码真实含义变得深奥且全局相关。增大 U-Net 网络的深度,会让模型的映射关系变得更为扭曲,而不利于学习训练。将扩散模型的主干模型从U-Net网络转化为 Transformer网络,让注意力层始终可以在一个更细粒度的尺度上实现全局的卷积和信息提取。因此,U-Net网络在架构设计上与 Transformer 网络产生性质上的区别,这一点可能是基于Transformer网络的扩散模型在更大规模的数据和模型尺寸下建模效果更好的原因。
(五)采样方式:确定性采样还是随机性采样
扩散模型的采样方式也在很大程度上影响表现,对于相同的扩散模型使用不同的采样方式会得到不同的采样分布。这其中会有几个维度的原因。
1. 计算精度
推断成本制约了采样过程中的求解器允许的模型评估次数(Number of forward evaluations, NFE),继而决定了求解的时间步长与精度。
2. 不完美的模型
受限于模型的设计,网络的设计,训练目标的拟定和权重设计,通过训练获得与真实数据分布的得分函数完全相同的模型是不可能的。
对一个训练完毕的扩散模型进行采样,需要拟定一个采样轨迹。根据 Fokker–Planck equation,与扩散过程的逆过程有相同概率密度的采样轨迹有无限种方案,它们符合以下的数学形式式:
d x t = ( f ( x t , t ) − ( g 2 ( t ) 2 + g w 2 ( t ) 2 ) s θ ( x t , t ) ) d t + g w ( t ) d w ˉ t dx_t = \left( f(x_t, t) - (\frac{g^2(t)}{2} + \frac{g_w^2(t)}{2}) s_\theta(x_t, t) \right) dt + g_w(t) d\bar{w}_t dxt=(f(xt,t)−(2g2(t)+2gw2(t))sθ(xt,t))dt+gw(t)dwˉt
式中 g w ( t ) g_w(t) gw(t) 为采样过程中注入的噪音幅值,当 g w ( t ) = 0 g_w(t) = 0 gw(t)=0,上式退化为常微分方程形式的确定性采样轨迹。
论文《Elucidating the Design Space of Diffusion-Based Generative Models》[6] 中论证了在采样过程中使用在数学上的真正含义。假如模型是真实数据分布的得分函数的完美建模,且假如求解器是不存在计算误差的,那么无论使用确定性采样还是随机性采样,都会是对同一个分布,也就是真实数据的分布,进行近似采样。一般而言,在实践中,使用某种噪音形式 g w ( t ) g_w(t) gw(t) 的随机性采样会比确定性采样有更好的采样质量。这是因为数学上,在时刻 t t t 注入幅值为 g w ( t ) g_w(t) gw(t) 的噪音,等价于将 g w ( t ) g_w(t) gw(t) 为噪音幅值,含有时刻 t t t 之前累积的来自于模型 s θ ( x t , t ) s_\theta(x_t, t) sθ(xt,t) 的重建信息的同时,使其比确定性采样更强的扰动, g w 2 ( t ) 2 s θ ( x t , t ) \frac{g^2_w(t)}{2} s_\theta(x_t, t) 2gw2(t)sθ(xt,t),引入当前时刻 t t t 的模型的重建信息。假如模型存在估计缺陷,比如对于时刻 t t t 之前的得分函数训练不充分,那么采用随机性采样可以在某种程度上纠正这种缺陷,并使用当前时刻 t t t 附近训练得到的方案得模型来作为为弥补。因此适度随机性采样在实践中是有益的。
论文《SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers》中的基线实验也重新证明了上述的观点,对于多种扩散过程,相比 ODE 的采样轨迹,SDE 的采样轨迹都显著取得了更好的表现。但因为SDE的求解器需要更大的模型评估次数,因此 ODE 的采样轨迹在采样速度层面具有显著优势。

3. 建模对象:隐空间中的扩散模型
受限于计算资源和硬件水平,即便是使用了最前沿的神经网络架构的扩散模型,它所能处理的数据维度也是有极限的。利用变分自动编码器(VAEs)对原数据进行低损编码,将其压缩至一个更小的隐空间的维度中,并在隐空间中使用扩散模型进行分布重建是一种可行且通用的做法。论文《Score-based Generative Modeling in Latent Space》中论述了如何联合训练“变分自动编码器-扩散模型”这种混合架构的训练方法。但在许多其它实践中,往往使用一个锁定模型参数,预先训练好的变分自动编码器即可。在诸如视频生成等超高维度的应用领域,在隐空间中建模对计算成本的节省无疑是巨大的。
四、总结
总的来说,以扩散模型为代表的生成式模型在近年来的技术进步是巨大的:
- 在理论层面上,研究者们建立了广义的扩散模型的理论框架,更好地定义了扩散过程的数学本质。
- 在算法层面,研究者们在模型训练目标、建模方式、采样方式等方面总结出了表现良好的各类算法,达成了初步的经验共识。
- 在模型层面,研究者们拓宽了扩散模型可选的技术方案,让其在更大规模的数据和参数下获得更好的模型表现成为可能。而在应用领域,扩散模型的前景方兴未艾。
在这个过程中,扩散模型为代表的生成式模型逐渐发展成为一种十分高效且具有巨大潜力的机器学习算法。这种突破性进展展望背后有两种内生的驱动力:
- 其一是因为在数学形式上的逻辑自洽和简洁优美会自动驱动后来的研究者们更好地继承之前的研究工作,更好地打造和统一理论框架。好的东西总是美的,晦涩难懂并不意味着原理更深邃,复杂的设计大一定是因为技术上更高明。
- 其二是扩散模型为代表的生成式模型贯彻了微分还原的方法论。如果说,扩散模型在理论上将一个复杂的 x x x 建模问题,弱化为了 d x dx dx 的建模问题,那么,在模型层面,使用诸如带有残差网络的注意力层等一些前沿的神经网络方法则进一步的建模变得更易于训练,从而这种方法在各类复杂应用场景下生效。
参考文献:透过 Diffusion Transformer 探索生成式模型的技术演进