链接:73. 矩阵置零 - 力扣(LeetCode)
题目:
给定一个
m x n的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。示例 1:
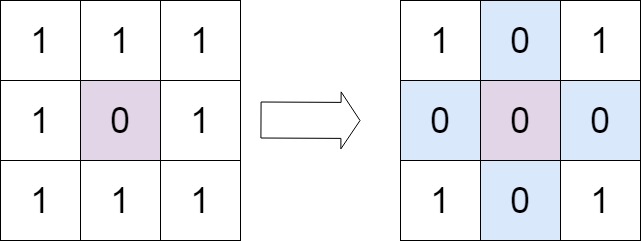
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
代码:
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var setZeroes = function(matrix) {
let m = matrix.length , n = matrix[0].length
let map = new Map()
for(let i = 0 ; i < m ; i++ ){
for(let j = 0 ; j<n ; j++ ){
if(matrix[i][j]==0){
map.set('i'+i,1)
map.set('j'+j,1)
// 将含0的行和列进行保存下来
}
}
}
for(let i = 0 ; i < m ; i++ ){
for(let j = 0 ; j<n ; j++ ){
if(map.get('i'+i)){
// 将含0的行的所有值置0
matrix[i][j] = 0
}else if(map.get('j'+j)){
// 将含0的列的所有值置0
matrix[i][j] = 0
}
}
}
};



![[Xshell] Xshell的下载安装使用及连接linux过程 详解(附下载链接)](https://i-blog.csdnimg.cn/direct/3e27ab7b15ba474e9ea0f0edb19e93b8.png)