零、LeetCode 原题

117. 填充每个节点的下一个右侧节点指针 II

一、题目描述

给定一个二叉树：

struct Node {int val;Node *left;Node *right;Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。

二、测试用例

示例 1：

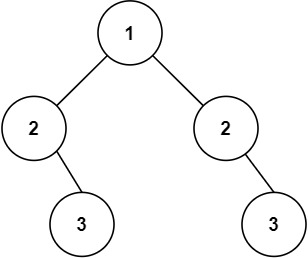
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

提示：

树中的节点数在范围 [0, 6000] 内
-100 <= Node.val <= 100

三、解题思路

3.1 层次遍历

1. 基本思路：
     使用队列进行层次遍历，为每一层的结点设置对应的后继结点；
2. 具体思路：
   • 定义：队列 q ；当前层结点数 curSzie ；下一层结点数 nextSize ；
   • 层次遍历：
     • 当前结点数为 0 ，表示一层就遍历结束了，然后将 nextSize 赋值给 curSize ；
     • 弹出一个结点，并且当前层结点数 curSize -- ；
     • 如果 curSize 不为 0 ，表示同层还有结点，所以当前结点的 next 就要指向队列头部的结点；
     • 如果存在左子树或者右子树，就将他们加入到队列尾部，并且下一层结点数 nextSize ++ ；

3.2 层次遍历（优化）

1. 基本思路：
     还是层次遍历，但是可以优化掉队列；当设置第 i 层的 next 指针时，第 i-1 层的 next 指针就已经设置好了，所以只要确定第 i-1 层的第 1 个结点就遍历该层的后续结点，可以替代掉队列；空间复杂度可以到达 $\mathrm{O}(1)$
2. 具体思路：
   • 获取第 i-1 层的开始结点；( i 从 2 开始，因为第一层就一个结点，不需要设置 next 指针 )
   • 遍历第 i-1 层：
     • 查找第 i 层的第 1 个结点；
     • 设置开始结点为第 1 个结点，即控制换层；
     • 为第 i 层设置 next 指针；

四、参考代码

4.1 层次遍历

时间复杂度：$\mathrm{O}(n)$
空间复杂度：$\mathrm{O}(n)$

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if (root == NULL)return NULL;queue<Node*> q;int curSize = 0, nextSize = 0;q.push(root);nextSize++;while (!q.empty()) {if (curSize == 0) {curSize = nextSize;nextSize = 0;}Node* t = q.front();q.pop();curSize--;if (curSize != 0)t->next = q.front();if (t->left != NULL) {q.push(t->left);nextSize++;}if (t->right != NULL) {q.push(t->right);nextSize++;}}return root;}
};

4.2 层次遍历（优化）

时间复杂度：$\mathrm{O}(n)$
空间复杂度：$\mathrm{O}(1)$

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if (root == NULL)return NULL;Node* start = root;while (start != NULL) {Node* p = start;Node* pre = NULL;while (p != NULL) { // 确定第 i 层的第一个结点if (p->left != NULL) {pre = p->left;break;} else if (p->right != NULL) {pre = p->right;break;} elsep = p->next;}start = pre;while (p != NULL) { // 设置第 i 层的 next 指针if (p->left != NULL && p->left != pre) {pre->next = p->left;pre = pre->next;}if (p->right != NULL && p->right != pre) {pre->next = p->right;pre = pre->next;}p = p->next;}}return root;}
};