代码随想录算法训练营第十一天（补）栈与队列| 后序表达式、滑动窗口、高频元素、链表总结

一、150. 逆波兰表达式求值

二、239. 滑动窗口最大值

三、347.前 K 个高频元素

四、总结

一、150. 逆波兰表达式求值

力扣题目链接(opens new window)

根据逆波兰表示法，求表达式的值。

有效的运算符包括 + , - , * , / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入: ["2", "1", "+", "3", " * "]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

 class Solution {public:int evalRPN(vector<string>& tokens) {stack<long long> st;for(int i=0;i<tokens.size();i++){if(tokens[i]=="+"||tokens[i]=="-"||tokens[i]=="*"||tokens[i]=="/"){long long num1=st.top();st.pop();long long  num2=st.top();st.pop();if(tokens[i]=="+") st.push(num2+num1);else if(tokens[i]=="-") st.push(num2-num1);else if(tokens[i]=="*") st.push(num1*num2);else if(tokens[i]=="/") st.push(num2/num1);}else{st.push(stoll(tokens[i]));}}int result=st.top();st.pop();return result;}};
注意是num2-num1

，在写代码的时候注意与实际的栈相结合

stoll:c++里把字符串直接转化成数字的函数

时间复杂度: O(n)
空间复杂度: O(n)

二、239. 滑动窗口最大值

力扣题目链接(opens new window)

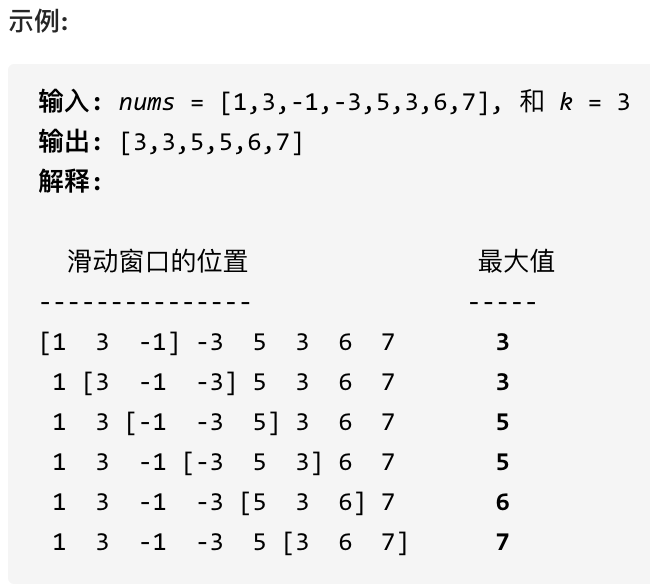
给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

提示：

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length

用栈实现滑动窗口，思想与数组实现一致——单调队列

 class Solution {private:class MYQueue{public :deque<int> que;void pop(int value){if(!que.empty()&&value==que.front()) que.pop_front();}void push(int value){while(!que.empty()&&value>que.back()) que.pop_back();que.push_back(value);}int front(){return que.front();}};public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MYQueue que;vector<int> result;for(int i=0;i<k;i++){que.push(nums[i]);}result.push_back(que.front());for(int i=k;i<nums.size();i++){que.pop(nums[i-k]);que.push(nums[i]);result.push_back(que.front());}return result;}};

三、347.前 K 个高频元素

力扣题目链接(opens new window)

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n \log n) , n 是数组的大小。
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。

class Solution {public:// 小顶堆class mycomparison {public:bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {return lhs.second > rhs.second;}};vector<int> topKFrequent(vector<int>& nums, int k) {// 要统计元素出现频率unordered_map<int, int> map; // map<nums[i],对应出现的次数>for (int i = 0; i < nums.size(); i++) {map[nums[i]]++;}// 对频率排序// 定义一个小顶堆，大小为kpriority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;// 用固定大小为k的小顶堆，扫面所有频率的数值for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {pri_que.push(*it);if (pri_que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为kpri_que.pop();}}// 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组vector<int> result(k);for (int i = k - 1; i >= 0; i--) {result[i] = pri_que.top().first;pri_que.pop();}return result;}};

时间复杂度: O(nlogk)
空间复杂度: O(n)