T1

写出图示信道的转移概率矩阵，并指出其是否为对称信道。

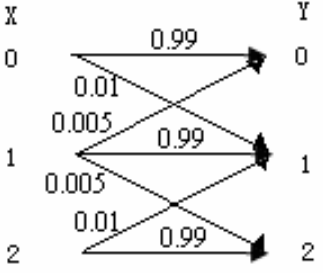
解：
信道的转移概率矩阵$P(Y|X)=\left[\begin{array}{ccc}0.99& 0.01& 0\\ 0.005& 0.99& 0.005\\ 0& 0.01& 0.99\end{array}\right]$
该信道不是对称信道。

T2

设二进制对称信道的概率转移矩阵为 $P=\left[\begin{array}{cc}2/3& 1/3\\ 1/3& 2/3\end{array}\right]$,

(1)若$p(x_0)=3/4,p(x_1)=1/4$ ,求 H(X), H(X/Y), H(Y/X)和 I(X; Y)。

(2)求该信道的信道容量及其达到信道容量时的输入概率分布。

解：(1)

$$p(x_0)=\frac{3}{4},p(x_1)=\frac{1}{4},H(X)=\frac{3}{4}\log \frac{4}{3}+\frac{1}{4}\log 4=0.811(bit/symbol)$$
$$P(Y\mid X)=\left[\begin{array}{cc}\frac{2}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{2}{3}\end{array}\right],P(XY)=\left[\begin{array}{cc}\frac{1}{2}& \frac{1}{4}\\ \frac{1}{12}& \frac{1}{6}\end{array}\right]$$
$$p(y_0)=\frac{1}{2}+\frac{1}{12}=\frac{7}{12},p(y_1)=\frac{1}{4}+\frac{1}{6}=\frac{5}{12}$$

$$H(XY)=\frac{1}{2}\log (2)+\frac{1}{4}\log (4)+\frac{1}{12}\log (12)+\frac{1}{6}\log (6)=1.73(bit/symbols)$$

$$H(Y)=\frac{7}{12}\log (\frac{12}{7})+\frac{5}{12}\log (\frac{12}{5})=0.98(bit/symbol)$$

$$H(X\mid Y)=H(XY)-H(Y)=1.73-0.98=0.75(bit/symbol)$$

$$H(Y|X)=H(XY)-H(X)=1.73-0.811=0.919(bit/symbol)$$

$$I(X;Y)=H(X)-H(X\mid Y)=0.811-0.75=0.061(bit/symbol)$$

(2)此信道为对称信道，则

$$\begin{array}{rl}& C=\log s-H\left(p_1^{\prime },p_2^{\prime },\cdots p_s^{\prime }\right)=\log (2)-H\left(\frac{2}{3},\frac{1}{3}\right)=\log 2+\frac{2}{3}\log \frac{2}{3}+\frac{1}{3}\log \frac{1}{3}\\ & =0.082(bit/symbol)\end{array}$$

达到信道容量时的输入概率分布为：$p(x_0)=p(x_1)=\frac{1}{2}$