论文名称：Generalizing to Unseen Domains: A Survey on Domain Generalization
论文下载：https://arxiv.org/abs/2103.03097
论文年份：2021
论文被引：78（2022/05/07）
论文代码：https://github.com/jindongwang/transferlearning/tree/master/code/DeepDG

论文总结

在这里插入图片描述

Abstract

Machine learning systems generally assume that the training and testing distributions are the same. T o this end, a key requirement is to develop models that can generalize to unseen distributions. Domain generalization (DG), i.e., out-of-distribution generalization, has attracted increasing interests in recent years. Domain generalization deals with a challenging setting where one or several different but related domain(s) are given, and the goal is to learn a model that can generalize to an unseen test domain. Great progress has been made in the area of domain generalization for years. This paper presents the first review of recent advances in this area. First, we provide a formal definition of domain generalization and discuss several related fields. We then thoroughly review the theories related to domain generalization and carefully analyze the theory behind generalization. We categorize recent algorithms into three classes: data manipulation, representation learning, and learning strategy, and present several popular algorithms in detail for each category. Third, we introduce the commonly used datasets, applications, and our open-sourced codebase for fair evaluation. Finally, we summarize existing literature and present some potential research topics for the future.

机器学习系统通常假设训练和测试分布是相同的。为此，一个关键要求是开发可以推广到看不见的分布的模型。近年来，域泛化（Domain generalization，DG），即分布外泛化（out-of-distribution generalization），引起了越来越多的兴趣。域泛化处理具有挑战性的设置，其中给出了一个或多个不同但相关的域，目标是学习一个可以泛化到看不见的测试域的模型。多年来，领域泛化方向取得了长足的进步。本文首次回顾了该领域的最新进展。首先，我们提供了领域泛化的正式定义并讨论了几个相关领域。然后，我们彻底回顾了与域泛化相关的理论，并仔细分析了泛化背后的理论。我们将最近的算法分为三类：数据操作、表示学习和学习策略，并针对每个类别详细介绍了几种流行的算法。第三，我们介绍了常用的数据集、应用程序和我们的开源代码库，以进行公平评估。最后，我们总结了现有的文献，并提出了一些未来的潜在研究课题。

1 INTRODUCTION

机器学习 (ML) 在计算机视觉、自然语言处理和医疗保健等各个领域取得了显著成功。 ML 的目标是设计一个模型，该模型可以从训练数据中学习一般性和预测性知识，然后将该模型应用于新的（测试）数据。传统的 ML 模型是基于独立同分布（identically and independently distributed，i.i.d）假设训练的，即训练和测试数据是相同且独立分布的。然而，这种假设在现实中并不总是成立。当训练数据和测试数据的概率分布不同时，ML模型的性能往往会因为域分布差距（domain distribution gaps ）而恶化[1]。收集所有可能领域的数据来训练 ML 模型是昂贵的，甚至是不可能的。因此，增强 ML 模型的泛化（generalization）能力在工业和学术领域都很重要。
在这里插入图片描述
有许多与泛化相关的研究课题，例如领域适应（domain adaptation）、元学习（meta-learning）、迁移学习（transfer learning）、协变量偏移（covariate shift）等。近年来，域泛化（Domain generalization，DG）备受关注。如图 1 所示，域泛化的目标是从一个或多个不同但相关的域（即不同的训练数据集）中学习一个模型，该模型将在未见的测试域上很好地泛化。例如，给定一个由来自草图、卡通图像和绘画的图像组成的训练集，域泛化需要训练一个良好的机器学习模型，该模型在对来自自然图像或照片的图像进行分类时具有最小的预测误差，这些图像显然具有明显的分布来自训练集中的图像。在过去的几年里，领域泛化在计算机视觉和自然语言处理等各个领域取得了重大进展。尽管取得了进展，但该领域还没有一项调查全面介绍和总结其主要思想、学习算法和其他相关问题，为未来提供研究见解。

在本文中，我们提出了关于域泛化的第一个调查，以介绍其最近的进展，特别关注其公式、理论、算法、研究领域、数据集、应用和未来的研究方向。我们希望本次调查能够为感兴趣的研究人员提供全面的回顾，并激发对该领域及相关领域的更多研究。

在我们论文的会议版本之后有几篇调查论文，与我们的有很大不同。[3] 写了一份关于 DG 的综述，而他们的重点是计算机视觉领域。[4] 最近发表的一篇关于分布外（out-of-distribution，OOD）泛化的综述论文。他们的工作集中在因果关系和稳定的神经网络上。一篇相关的调查论文 [5] 用于 OOD 检测，而不是构建可应用于任何看不见的环境的工作算法。

这篇论文是我们之前在 IJCAI-21 调查轨道上接受的短篇论文的大幅扩展版本（6 页，包含在附录文件中）。与短篇论文相比，该版本做了以下扩展：

我们提出了域泛化和相关域适应（domain generalization and the related domain adaptation）的理论分析。
我们通过添加新类别大大扩展了该方法：例如，因果关系启发方法（causality-inspired methods）、特征解耦（feature disentanglement）的生成建模、不变风险最小化（invariant risk minimization）、基于梯度操作的方法（gradient operation-based methods）和其他学习策略，以全面总结这些 DG 方法。
对于所有类别，我们通过包括更多相关的算法、比较和讨论来扩大对方法的分析。我们还包括最近的论文（超过 30% 的新工作）。
我们扩展了数据集和应用程序的范围，我们还探索了领域泛化的评估标准。最后，我们构建了一个名为 DeepDG1 的用于 DG 研究的开源代码库，并对公共数据集的结果进行了一些分析。

本文组织如下。我们在第 2 节中阐述了域泛化问题并讨论了它与现有研究领域的关系。第 3 节介绍了域泛化的相关理论。在第 4 节中，我们详细描述了一些具有代表性的 DG 方法。在第 5 节中，我们展示了一些从传统环境扩展而来的新的 DG 研究领域。第 6 节介绍应用，第 7 节介绍 DG 的基准数据集。我们总结了现有工作的见解，并在第 8 节中提出了一些可能的未来方向。最后，我们在第 9 节总结了本文。

2 BACKGROUND

2.1 Formalization of Domain Generalization

在本节中，我们将介绍本文中使用的符号和定义。

定义 1：域（Domain）。令 $\mathcal{X}$ 表示非空输入空间， $\mathcal{Y}$ 表示输出空间。域由从分布中采样的数据组成。我们将其表示为 $\mathcal{S} = {(x_i, y_i)}^n_{i=1} ∼ P_{XY}$ ，其中， $\mathbf{x} ∈ \mathcal{X} ⊂ \R^d, y ∈ \mathcal{Y} ⊂ \R$ 表示标签， $P_{XY}$ 表示输入样本和输出标签的联合分布。 $X$ 和 $Y$ 表示相应的随机变量。
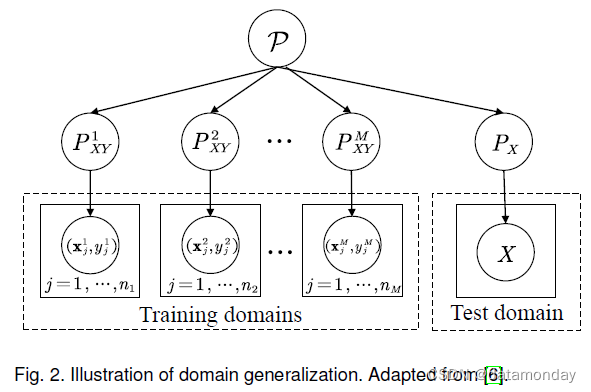
在这里插入图片描述
定义 2：域泛化（Domain generalization）。如图 2 所示，在域泛化中，给定 $M$ 个训练（源）域 $\mathcal{S}_{train} = \{\mathcal{S}^i | i = 1, · · · , M\}$ 其中 $\mathcal{S}^i = \{(x^i_j, y^i_j)\}^{n_i}_j=1$ 表示第 $i$ 个域。每对域之间的联合分布不同： $P^i_{XY} \neq P^j_{XY}, 1 ≤ i \neq j ≤ M$ 。域泛化的目标是从 $M$ 个训练域中学习鲁棒且可泛化的预测函数 $\mathcal{X} → \mathcal{Y}$ ，以在看不见的测试域 $\mathcal{S}_{test}$ 上实现最小预测误差（即，在训练中不能访问 $\mathcal{S}_{test}$ 并且 $P^{test}_{XY} \neq P^i_{XY} \ for \ i ∈ \{1, · · · , M\}$ ）。
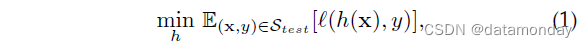
在这里插入图片描述
其中 $\mathbb{E}$ 是期望值， $\mathscr{l}(·,·)$ 是损失函数。

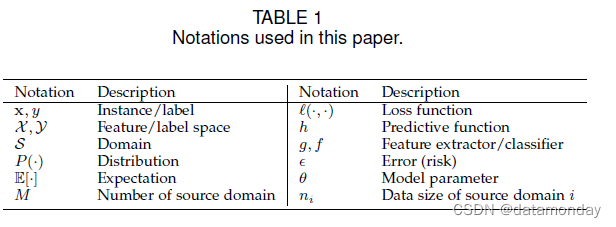
我们在表 1 中列出了常用的符号。
在这里插入图片描述

2.2 Related Research Areas

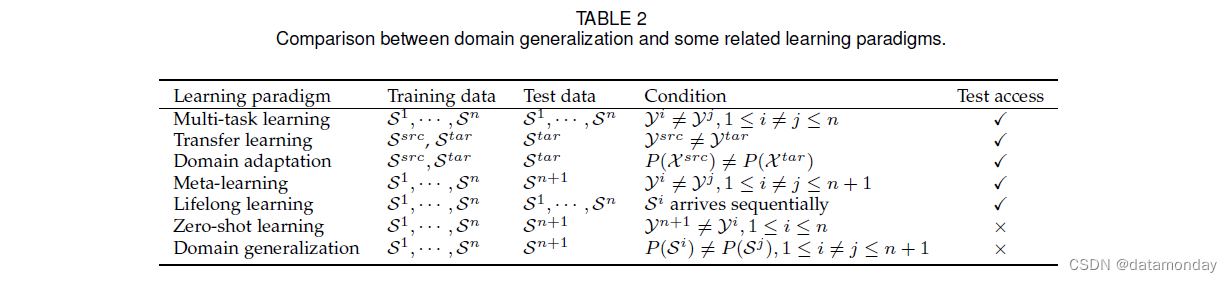
在这里插入图片描述
与域泛化密切相关的研究领域包括但不限于：迁移学习 (transfer learning)、域适应 (domain adaptation)、多任务学习 (multi-task learning)、多领域学习 (multiple domain learning)、元学习 (meta-learning)、终身学习 (lifelong learning) 和零样本学习 (zero-shot learning)。我们在表 2 中总结了它们与域泛化的差异，并在下面简要描述了它们。

多任务学习（Multi-task learning） [7] 联合优化几个相关任务的模型。通过在这些任务之间共享表示，可以使模型更好地泛化原始任务。请注意，多任务学习的目的不是增强对新（看不见的）任务的泛化能力。特别是，多域学习（multi-domain learning）是一种多任务学习，它在多个相关域上进行训练，为每个原始域 [8] 学习好的模型，而不是新的测试域。

迁移学习（Transfer learning） [9, 10, 11] 在源任务上训练模型，旨在提高模型在不同但相关的目标域/任务上的性能。 Pretraining-finetuning 是迁移学习的常用策略，其中源域和目标域具有不同的任务，并且在训练中访问目标域。在 DG 中，无法访问目标域，训练和测试任务通常相同，但分布不同。

域适应 (Domain Adaptation, DA) [12, 13] 近年来也很流行。 DA 旨在使用现有的训练源域最大化给定目标域的性能。DA 和 DG 的区别在于 DA 可以访问目标域数据，而 DG 在训练期间看不到它们。这使得 DG 比 DA 更具挑战性，但在实际应用中更加现实和有利。

元学习（Meta-learning） [14,15,16] 旨在通过从以前的经验或任务中学习来学习学习算法本身，即学习学习（learning-to-learn）。虽然元学习中的学习任务不同，但域泛化中的学习任务是相同的。元学习是一种通用的学习策略，可用于 DG [17,18,19,20]，通过在训练域中模拟元训练和元测试任务来提高 DG 的性能。

终身学习（Lifelong Learning）[21]，或持续学习（continual learning），关心多个连续领域/任务之间的学习能力。它要求模型通过适应新知识，同时保留以前学习的经验，随着时间的推移不断学习。这也与 DG 不同，因为它可以在每个时间步访问目标域，并且它没有显式处理跨域的不同分布。

零样本学习（Zero-shot learning） [22, 23] 旨在从已见类别中学习模型，并对训练中未见类别的样本进行分类。相比之下，域泛化通常研究训练和测试数据来自同一类但分布不同的问题。

3 THEORY

在本节中，我们回顾了一些与域泛化相关的理论。由于域适应与 DG 密切相关，我们从域适应理论开始。

3.1 Domain Adaptation

对于二元分类问题，我们将源域上的真实标注函数表示为 $h^{∗s} : \mathcal{X} → [0, 1]$ （当输出在 (0, 1) 时，表示 y = 1 的概率），将目标域上的真实标注函数表示为 $h^{∗t}$ 。令 $\mathcal{X} → [0, 1]$ 是假设空间 $\mathcal{H}$ 中的任何分类器。两个分类器 $h$ 和 $h^{'}$ 在源域上的分类差异可以通过以下方式测量
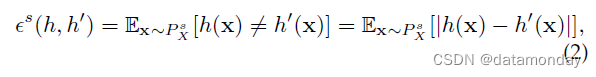
在这里插入图片描述
类似地，我们可以在期望 $P^t_X$ 时定义 $\epsilon_t$ 。定义 $\epsilon^s(h) := \epsilon^s(h, h^{∗s})$ 和 $\epsilon^t(h) := \epsilon^t(h, h^{∗t})$ 分别作为分类器 $h$ 在源域和目标域上的风险（risk）。

DG/DA 的目标是最小化目标风险 $\epsilon^t(h)$ ，但由于没有关于 $h^{∗t}$ 的任何信息，所以无法访问。因此，人们寻求使用可处理的源风险 $\epsilon^s(h)$ 来限制目标风险 $\epsilon^t(h)$ 。[24] (Thm. 1) 给出了两个风险的界限：
在这里插入图片描述
然而，总变化是一个很大的距离（即，它往往非常大），可能会放松界限（4），并且很难使用有限样本进行估计。为了解决这个问题，[24] 开发了另一个界限（[24]，Thm. 2；[25]，Thm. 1）：

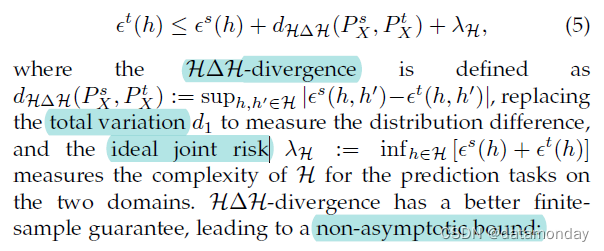
定理 1：域适应误差界（非渐近），Domain adaptation error bound (non-asymptotic) [24]（Thm. 2）。令 $d$ 为 $\mathcal{H}$ 的 Vapnik-Chervonenkis (VC) 维度 [26]， $\mathcal{U}^s$ 和 $\mathcal{U}^t$ 为来自两个域的大小为 $n$ 的未标记样本。那么对于任何 $\mathcal{H}$ 和 $δ \in (0, 1)$ ，以下不等式以至少 $1 - δ$ 的概率成立：
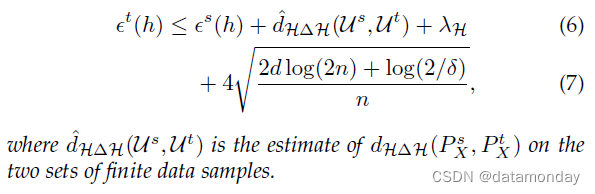
在这里插入图片描述
在上述范围内，域分布差异 $d(P^s_X, P^t_X)$ 是不可控的，但是可以学习一个表示函数 $\mathcal{X} → \mathcal{Z}$ 将原始输入数据 $\mathbf{x}$ 映射到某个表示空间 $\mathcal{Z}$ ，使得表示两个域的分布越来越接近。DA 的这个方向因此被称为基于域不变表示（DA-DIR，domain-invariant representation）的 DA。从那以后，域不变表示的理论启发了许多 DA/DG 方法，这可以在第 4.2 节中看到。

3.2 Domain Generalization

3.2.1 Average risk estimation error bound

域泛化理论的第一线考虑了目标域完全未知的情况（甚至没有无监督数据），并测量所有可能目标域的平均风险。假设所有可能的目标分布都遵循 $(\mathbf{x}, y)$ 分布上的潜在超分布 (hyper-distribution) $\mathcal{P}：P^t_{XY} ∼ \mathcal{P}$ ，并且源分布也遵循相同的超分布： $P^1_{XY}，···，P^M_{XY} ∼ \mathcal{P}$ 。任何可能的目标域，在这种情况下要学习的分类器也将域信息 $P_X$ 包含在其输入中，因此预测在具有分布 $P_{XY}$ 的域上采用 $h(P_X, \mathbf{x})$ 的形式。对于这样的分类器 $h$ ，它在所有可能的目标域上的平均风险由下式给出：
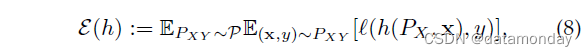
在这里插入图片描述
其中 $\mathscr{l}$ 是 $\mathcal{Y}$ 上的损失函数。准确评估期望是不可能的，但我们可以使用 $\mathcal{P}$ 之后的有限域/分布和每个分布之后的有限 $(x, y)$ 样本来估计它。正如我们假设 $P^1_{XY}，···，P^M_{XY} ∼ \mathcal{P}$ 一样，源域和监督数据可用于此估计：
在这里插入图片描述
要考虑的第一个问题是这种估计与目标 $\mathcal{E}(h)$ 的近似程度。这可以通过在 $h$ 的某个空间上 $\mathcal{E}(h)$ 和 $\hat{\mathcal{E}}(h)$ 之间的最大差异来衡量。据我们所知，这是由 [6] 首先分析的，其中 $h$ 的空间被视为再现核希尔伯特空间（reproducing kernel Hilbert space，RKHS）。但是，不同于一般的处理，这里的分类器 $h$ 也依赖于分布 $P_X$ ，所以定义 RKHS 的核应该是 $\bar{k}((P^1_X, \mathbf{x}_1), (P^2_X, \mathbf{x}_2))$ 的形式。[6] 使用 $\mathcal{X}$ 上的核 $k_X$ 、 $k'_X$ 和核 $k'_X$ 的 RKHS $\mathcal{H}_{k'_X}$ 上的核 $\kappa$ 构造这样的核： $\bar{k}((P^1_X, \mathbf{x}_1), (P^2_X, \mathbf{x}_2)) := κ(Ψ_{k'_X} (P^1_X) ), Ψ_{k'_X} (P^2_X))k_X(\mathbf{x}_1, \mathbf{x}_2)$ ，其中 $Ψ_{k'_X} (P_X) := E_{\mathbf{x}}∼P_X [k'_X(\mathbf{x}, ·)] ∈ \mathcal{H}_{k'_X}$ 是分布 $P_X$ 通过核 $k^{'}$ 的核嵌入（kernel embedding）。结果由以下定理给出，该定理给出了核 $\bar{k}$ 的 RKHS $\mathcal{H}_{\bar{k}}$ 中半径为 $r$ 的以原点为中心的封闭球 $\mathcal{B}_{\mathcal{H}_{\bar{k}}}(r)$ 内的最大平均风险估计误差的界线，略简化情况，其中 $n^1 = · · · = n^M =：n.$

定理 2：二分类的平均风险估计误差界限，Average risk estimation error bound for binary classification [6]。假设损失函数 $\mathscr{l}$ 在它的第一个参数中是 $L_{\mathscr{l}}-Lipschitz$ 并且以 $B_{\mathscr{l}}$ 为界。还假设核 $k_X$ 、 $k'_X$ 和 $\kappa$ 分别以 $B^2_k$ 、 $B^2_{k'} ≥ 1$ 和 $B^2_{κ}$ 为界，并且典型特征图 $Φ_κ : v ∈ \mathcal{H}_{k'_X} → κ(v, ·) ∈ \mathcal{H}_κ$ 的 $κ$ 是 $L_κ-Holder$ 在封闭球 $\mathcal{B}_{\mathcal{H}_{k'_X}} (B_{k'})$ 上的阶 $α \in (0, 1]$ 。那么对于任何 $r > 0$ 和 $δ \in (0, 1)$ ，概率至少为 $1 - δ$ ，它认为：
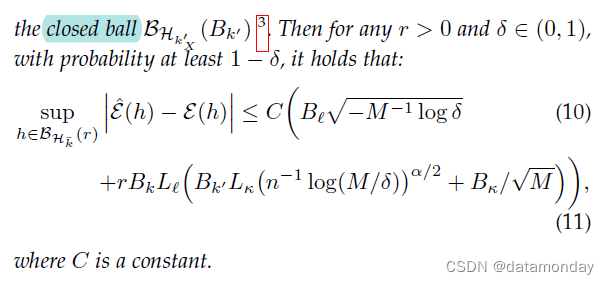
在这里插入图片描述
如果将 $(M, n)$ 替换为 $(1, M n)$ ，则界限通常会变大。这表明使用域数据集比仅仅将它们汇集到一个混合数据集中更好，因此域信息发挥了作用。这个结果后来在 [27] 中得到了扩展，[28] 以类似的形式给出了多类分类的界限。

3.2.2 Generalization risk

DG 理论的另一条线在协变量偏移的假设下考虑特定目标域的风险（即，标记函数 $h^*$ 或 $P_{Y|X}$ 在所有域上都是相同的）。这种测量类似于3.1 节域适应理论中考虑的测量，因此我们对源风险 $\epsilon^1, ..., \epsilon^M$ 和目标风险 $\epsilon^t$ 采用相同的定义。在协变量移位 (covariate shift) 假设下，每个域由 $\mathcal{X}$ 上的分布来表征。[102] 然后考虑在源域分布的凸包 (convex hull) 内近似目标域分布 $P^t_X： Λ := \{\sum^M_{i=1} π_iP^i_X | π ∈ ∆_M\}$ ，其中 $∆ M$ 是 (M - 1) 维单纯形 (simplex)，因此每个 $π$ 代表一个归一化的混合权重。与域适应情况类似，分布差异由 $\mathcal{H}$ -散度测量，以包括分类器类别的影响。

定理 3：域泛化误差界（Domain generalization error bound） [102]。
在这里插入图片描述
其中 $λ_{\mathcal{H}}, (P^t_X ,P^∗_X)$ 是跨目标域和具有最佳逼近分布 $P^∗_X$ 的域的理想联合风险。

当有多个源域时，结果可以看作是第 3.1 节中域适应边界的泛化。再次类似于域适应情况，这个界激发了基于域不变表示的域泛化方法，它同时最小化了对应于界的第一项的所有源域的风险，以及源域和目标域之间的表示分布差异希望减少表示空间上的 $γ$ 和 $ρ$ 。总而言之，泛化理论是一个活跃的研究领域，其他研究人员也利用信息量 [167] 和对抗训练 [102, 98, 167, 28] 推导出了不同的 DG 理论界限。

4 METHODOLOGY

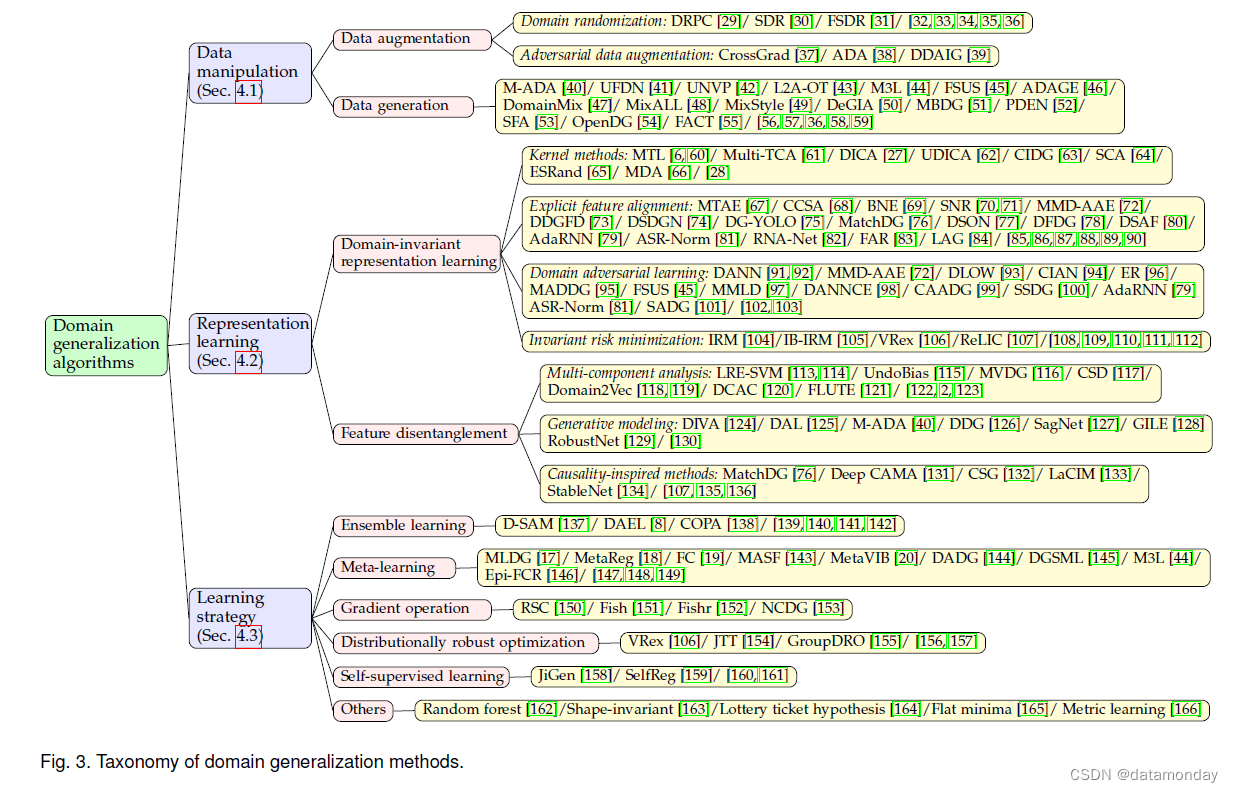
在这里插入图片描述
在本节中，我们将详细介绍现有的域泛化方法。如图 3 所示，我们将它们分为三组，即：

1）数据操纵：这类方法侧重于操纵输入以帮助学习一般表示。沿着这条线，有两种流行的技术：

a）数据增强，主要基于输入数据的增强、随机化和变换；
b）数据生成，生成不同的样本以帮助泛化。

2）表示学习：这类方法在域泛化中是最流行的。有两种代表性技术：

a）域不变表示学习，它执行内核、对抗训练、域之间的显式特征对齐或不变风险最小化来学习域不变表示；
b）特征解耦，它试图将特征解耦为域共享或特定域的部分，以便更好地泛化。

3）学习策略：这类方法侧重于利用通用学习策略来提升泛化能力，主要包括以下几种方法：

a）集成学习，它依靠集成的力量来学习一个统一的、泛化的预测函数；
b）元学习，基于学习到学习的机制，通过构建元学习任务来模拟域迁移来学习一般知识；
c）梯度操作，试图通过直接对梯度进行操作来学习广义表示；
d）分布鲁棒优化，学习训练域的最坏情况分布场景；
e）自监督学习，它构建代理任务来学习广义表示。此外，还有其他可用于 DG 的学习策略。

这三类方法在概念上是不同的。它们相辅相成，可以结合起来实现更高的性能。我们将在下文详细描述每个类别的方法。

4.1 Data Manipulation

我们总是渴望获得更多机器学习 (ML) 中的训练数据。ML 模型的泛化性能通常取决于训练数据的数量和多样性。给定一组有限的训练数据，数据操作是生成样本以增强模型泛化能力的最便宜、最简单的方法之一。基于数据操作的 DG 的主要目标是使用不同的数据操作方法增加现有训练数据的多样性。同时，数据量也随之增加。数据增强或生成技术可以增强模型的泛化能力，但 Adila 和 Kang [168] 的实验表明，该模型倾向于基于 NLP 任务的简单句法启发式对 OOD 和分布样本进行预测。

我们将基于数据操作的 DG 的一般学习目标制定为：
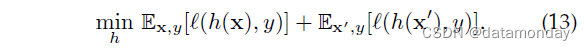
在这里插入图片描述
其中 x‘ = M(x) 表示使用函数 M(·) 处理的数据。基于此函数的差异，我们将现有工作进一步分为两类：数据增强和数据生成。

4.1.1 Data augmentation-based DG

增强是训练机器学习模型最有用的技术之一。典型的增强操作包括翻转、旋转、缩放、裁剪、添加噪声等。它们已广泛用于监督学习，以通过减少过拟合来提高模型的泛化性能 [169, 36]。无一例外，它们也可以用于 DG，其中 M(·) 可以被实例化为这些数据增强函数。

4.1.1.1 Domain randomization

域随机化：除了典型的增强之外，域随机化是一种有效的数据增强技术。它通常是通过基于有限的训练样本生成可以模拟复杂环境的新数据来完成的。这里，M(·) 函数被实现为几个手动变换（常用于图像数据），例如：改变物体的位置和纹理，改变物体的数量和形状，修改光照和相机视图，以及添加不同的数据的随机噪声类型。

[32] 首先使用这种方法从模拟环境中生成更多的训练数据，以便在真实环境中进行泛化。
[33,34,35,29] 中也使用了类似的技术来增强模型的泛化能力。
[30] 在随机放置对象进行数据生成时进一步考虑了场景的结构，这使神经网络能够在检测对象时学会利用上下文。
[58] 提出不仅要增加特征，还要增加标签。

不难看出，通过随机化，可以增加样本的多样性。但随机化往往是随机的，这表明可能存在一些无用的随机化，可以进一步去除以提高模型的效率。

4.1.1.2 Adversarial data augmentation

对抗性数据增强：对抗性数据增强旨在通过增强数据的多样性同时确保其可靠性来引导增强以优化泛化能力。

[37] 使用贝叶斯网络对标签、域和输入实例之间的依赖关系进行建模，并提出了 CrossGrad，这是一种谨慎的数据增强策略，它沿着最大域变化的方向扰动输入，同时尽可能少地改变类标签。
[38] 提出了一种迭代过程，该过程使用来自当前模型下“困难(hard)”的虚构目标域的示例来增强源数据集，其中在每次迭代时附加对抗性示例以启用自适应数据增强。
[39] 对抗性地训练了一个用于数据增强的转换网络，而不是通过梯度上升直接更新输入，而他们在 [170, 31] 中采用了弱增强和强增强的正则化。

对抗性数据增强通常具有某些可供网络使用的优化目标。然而，其优化过程往往涉及对抗性训练，因此比较困难。

4.1.2 Data generation-based DG

数据生成也是一种流行的技术，可以生成多样化和丰富的数据，以提高模型的泛化能力。在这里，函数 M(·) 可以使用一些生成模型来实现，例如变分自动编码器 (VAE) [171] 和生成对抗网络 (GAN) [172]。此外，还可以使用 Mixup [173] 策略来实现。

[56] 使用 ComboGAN [174] 生成新数据，然后应用 MMD [175] 等域差异度量来最小化真实图像和生成图像之间的分布差异，以帮助学习一般表示。
[40] 利用对抗训练来创建“虚构”但“具有挑战性”的群体，其中使用 Wasserstein 自动编码器 (WAE) [176] 来帮助生成保留语义并具有大域传输的样本。
[43] 在语义一致性下生成新分布，然后最大化源分布和新分布之间的差异。
[57] 引入了一种基于图像风格化的简单转换，以探索跨源可变性以获得更好的泛化效果，其中 AdaIN [177] 用于实现对任意风格的快速风格化。
与其他人不同，[52] 使用对抗训练来生成域而不是样本。

这些方法比较复杂，因为涉及到不同的生成模型，我们应该注意模型容量和计算成本。

除了上述生成模型，Mixup [173] 也是一种流行的数据生成技术。Mixup 通过在任意两个实例之间以及它们的标签之间执行线性插值来生成新数据，其中权重从 Beta 分布中采样，这不需要训练生成模型。最近，有几种方法将 Mixup 用于 DG，通过在原始空间 [47、48、54] 中执行 Mixup 来生成新样本；或者在特征空间 [49, 148, 55] 中没有明确生成原始训练样本。这些方法在流行的基准测试中取得了可喜的性能，同时在概念上和计算上保持简单。

4.2 Representation Learning

几十年来，表示学习一直是机器学习的重点[178]，也是领域泛化成功的关键之一。我们将预测函数 $h$ 分解为 $h = f ◦ g$ ，其中 $g$ 是表示学习函数， $f$ 是分类器函数。表示学习的目标可以表述为：
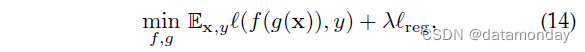
在这里插入图片描述
其中 $\mathscr{l}_{reg}$ 表示一些正则化项， $λ$ 是权衡参数。许多方法旨在更好地学习特征提取函数 g 与相应的 $\mathscr{l}_{reg}$ 。在本节中，我们根据不同的学习原理将有关表示学习的现有文献分为两大类：域不变表示学习和特征解耦。

4.2.1 Domain-invariant representation-based DG

[179] 的工作从理论上证明，如果特征表示对不同的域保持不变，则表示是通用的并且可以转移到不同的域（另请参阅第 3 节）。基于这一理论，已经提出了许多用于域适应的算法。类似地，对于域泛化，目标是减少特定特征空间中多个源域之间的表示差异，使其保持域不变，从而使学习模型能够对未见域具有泛化能力。沿着这条线，主要有四种类型的方法：基于内核的方法、领域对抗学习、显式特征对齐和不变风险最小化。

4.2.1.1 Kernel-based methods

基于核的方法：基于核的方法是机器学习中最经典的学习范式之一。基于核的机器学习依赖核函数将原始数据转换为高维特征空间，而无需计算该空间中数据的坐标，而是通过简单地计算特征中所有对的样本之间的内积空间。最具代表性的基于内核的方法之一是支持向量机（SVM）[180]。对于域泛化，有很多基于核方法的算法，其中表示学习函数 g 被实现为一些特征图 φ(·)，使用 RBF 核和拉普拉斯核等核函数 k(·,·) 很容易计算。

[6] 首次使用核方法进行域泛化，并在 [60] 中对其进行了扩展。他们采用半正定核学习（positive semi-definite kernel learning）从训练数据中学习域不变核。
[61] 采用传输分量分析 (transfer component analysis，TCA) [181] 来桥接多域距离，使 DG 更接近。
与 TCA 的核心思想类似，域不变分量分析 (DICA) [27] 是使用内核进行 DG 的经典方法之一。DICA 的目标是找到一个特征变换核 k(·,·)，以最小化特征空间中所有数据之间的分布差异。
[62] 采用了与 DICA 类似的方法，并进一步增加了属性正则化。
与处理边际分布的 DICA 相比，[63] 学习了具有域不变类条件分布的特征表示。
散点成分分析 (Scatter component analysis, SCA) [64] 采用Fisher的判别分析来最小化来自同一类和相同域的表示的差异，并最大化来自不同类和不同域的表示的差异。
[65] 提出了一种椭圆汇总随机化 (Elliptical Summary Randomisation, ESRand)，它由随机内核和椭圆数据汇总组成。ESRand 将每个域投影到一个椭圆中来表示域信息，然后使用一些相似度度量来计算距离。
[66] 提出了多域判别分析来对 DG 执行分类内核学习，这更细粒度。

综上所述，这类方法往往与其他类别高度相关，作为它们的发散度量或理论支持。

4.2.1.2 Domain adversarial learning

域对抗学习：领域对抗训练被广泛用于学习领域不变特征。

[91] 和 [92] 提出了用于域适应的域对抗神经网络 (DANN)，它对生成器和判别器进行对抗训练。鉴别器被训练来区分域，而生成器被训练来欺骗鉴别器以学习域不变的特征表示。[72] 对 DG 采用了这种想法。
[93] 通过逐渐减少流形空间（manifold space）中的域差异来使用对抗训练。
[94] 提出了一种条件不变对抗网络（CIAN）来学习 DG 的分类对抗网络。 [95, 99, 103] 中也使用了类似的想法。
[100] 使用单面对抗学习（single-side adversarial learning）和不对称三元组损失（asymmetric triplet loss）来确保只有来自不同域的真实人脸 (real face) 是无法区分的，但对于假人脸 (fake face) 则不然。之后，提取的假人脸特征在特征空间中比以前更分散，而真实人脸的特征更聚集，从而为看不见的域提供更好的泛化类边界。
除了对抗性域分类，[96] 通过最小化不同训练域的条件分布之间的 KL 散度引入了额外的熵正则化，以推动网络学习域不变特征。
还提出了一些其他基于 GAN 的方法 [45, 98, 102]，理论上保证了泛化界限。

4.2.1.3 Explicit feature alignment

显式特征对齐：这一系列工作通过显式特征分布对齐 [72、182、183、184] 或特征归一化 [185、186、187、70] 跨源域对齐特征以学习域不变表示。

[68] 为表示学习引入了跨域对比损失，其中映射域在语义上对齐，但最大程度地分离。
一些方法通过最小化最大平均差异（maximum mean discrepancy，MMD）[188, 181, 189, 190]，二阶相关性（second order correlation）[191, 192, 193]，均值和方差（矩匹配）[183]，Wasserstein 距离 [182] 等显式地最小化特征分布差异，用于域适应或域泛化的域。
[182] 通过最小化 Wasserstein 距离以实现域不变特征空间，通过最优传输对齐不同源域的边缘分布。

此外，还有一些作品使用特征归一化技术来增强域泛化能力 [185, 186]。

[185] 将实例归一化 (Instance Normalization, IN) 层引入 CNN，以提高模型的泛化能力。 IN 已在图像风格转移领域进行了广泛的研究 [194, 195, 177]，其中图像的风格由 IN 参数反映，即每个特征通道的均值和方差。因此，IN 层 [196] 可用于消除特定于实例的样式差异以增强泛化 [185]。然而，IN 与任务无关，可能会删除一些区分信息。
在 IBNNet 中，IN 和批量归一化 (BN) 并行使用以保留一些判别信息 [185]。
在 [187] 中，BN 层被 Batch Instance Normalization (BIN) 层取代，BIN 层通过选择性地使用 BN 和 IN 来自适应地平衡每个通道的 BN 和 IN。
[70, 71] 提出了一种风格归一化和恢复 (SNR) 模块，以同时确保网络的高泛化和辨别能力。在通过 IN 进行样式归一化之后，执行恢复步骤以从残差中提取与任务相关的判别特征（即原始特征和样式归一化特征之间的差异）并将它们添加回网络以确保高判别性。
恢复原状的想法被扩展到其他基于对齐的方法，以恢复对齐丢弃的有用的判别信息[83]。
最近，[80] 将 IN 应用于无监督 DG，其中训练域中没有标签来获取不变和可迁移的特征。
[81] 中提出了不同归一化技术的组合，以表明自适应学习归一化技术可以提高 DG。

这类方法更灵活，可以应用于其他类型的类别。

4.2.1.4 Invariant risk minimization (IRM)

不变风险最小化 (IRM)：[104] 考虑了关于域泛化表示的域不变性的另一种观点。他们并不寻求匹配所有域的表示分布，而是强制表示空间顶部的最优分类器在所有域中都相同。直觉是预测的理想表示是 y 的原因，因果机制不应受其他因素/机制的影响，因此是域不变的。形式上，IRM 可以表述为：
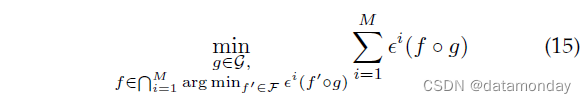
在这里插入图片描述
对于 g 的某些函数类 F 和 f 的 F。 f 的约束体现了所有域共享相同表示级别分类器的要求，目标函数鼓励 f 和 g 实现低源域风险。然而，这个问题很难解决，因为它在约束中涉及到一个内部优化问题。然后作者开发了一个代理问题来学习更实用的特征提取器 g：
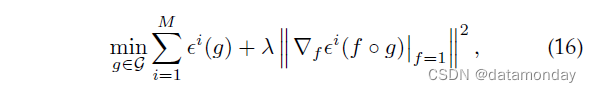
在这里插入图片描述
其中考虑了一个虚拟的表示级分类器 f = 1，梯度范数项衡量了该分类器的最优性。这项工作还提出了一个可能强线性假设下的泛化理论，即对于足够多的源域，可以识别真实不变分类器。

IRM 最近获得了显著的知名度。对 IRM [111] 的成功 [112] 和失败案例有一些进一步的理论分析，并且 IRM 已扩展到其他任务，包括文本分类 [110] 和强化学习 [197]。也扩展了追求最优表示级分类器不变性的思想。

[106] 通过最小化源域之间的外推风险来促进这种不变性，这基本上最小化了源域风险的方差。
[107] 旨在在自监督设置中学习这种表示，其中第二个域是通过显示各种语义无关变化的数据增强构建的。
最近，[105] 发现仅 f 的不变性是不够的。他们发现，如果 g 捕获“信息充分的不变特征”，IRM 仍然会失败，这使得 y 在所有域上都独立于 x。分类（与回归）任务尤其如此。因此引入了信息瓶颈正则化（information bottleneck regularization）以仅维护部分信息特征。

4.2.2 Feature disentanglement-based DG

解耦表示学习（Disentangled representation learning）旨在学习将样本映射到特征向量的函数，该特征向量包含有关不同变化因素的所有信息，并且每个维度（或维度的子集）仅包含有关某些因素的信息。基于解耦的 DG 方法通常将特征表示分解为可理解的组合/子特征，其中一个特征是共享域/不变特征，另一个是特定域的特征。基于解耦的 DG 的优化目标可以概括为：
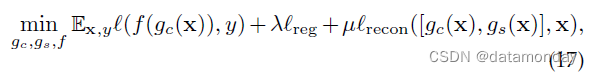
在这里插入图片描述
其中 gc 和 gs 分别表示共享域和特定域的特征表示。 λ 和 μ 是权衡参数。损失lreg 是一个正则化术语，明确鼓励域共享和特定特征的分离，lrecon表示防止信息丢失的重建损失。注意 [gc(x), gs(x)] 表示两种特征的组合（不限于串联(concatenation)操作）。

基于网络结构和实现机制的选择，基于解耦的 DG 主要可分为三类：多分量分析、生成建模和因果关系启发方法。

4.2.2.1 Multi-component analysis

多分量分析：在多分量分析中，通常使用共享域和特定域的网络参数来提取共享域和特定域的特征。

UndoBias [115] 的方法从 SVM 模型开始，以最大化所有训练数据的区间分类以进行域泛化。他们将第 i 个域的参数表示为 wi = w0 + Δi，其中 w0 表示域共享参数，Δi 表示域特定参数。其他一些方法从不同方面扩展了 UndoBias 的思想。
[116] 提出使用多视图学习进行域泛化。他们提出了多视图 DG (MVDG) 来学习不同视图下示例 SVM 的组合，以实现稳健的泛化。
[122] 为每个域设计了特定于域的网络，并为所有域设计了一个共享的域不变网络来学习解耦的表示，其中采用低秩重构以结构化的低秩方式对齐两种类型的网络。
[2] 将 UndoBias 的思想扩展到神经网络上下文中，并开发了一种用于端到端训练的低秩参数化 CNN 模型。
[123] 通过手动比较来自不同领域的某些区域的注意力热图来学习解耦的表示。还有其他作品采用多成分分析进行解耦 [118, 113, 114, 117, 121, 198, 199, 200, 119]。

一般来说，多分量分析可以在不同的体系结构中实现，并且对于解耦表示仍然有效。

4.2.2.2 Generative modeling

生成式建模：生成式模型可用于从数据生成过程的角度进行解耦。这种方法试图从域级、样本级和标签级来制定样本的生成机制。

一些工作进一步将输入分解为与类无关的特征，其中包含与特定实例相关的信息[201]。
域不变变分自动编码器 (DIVA) [124] 将特征分解为域信息、类别信息和其他信息，这些信息是在 VAE 框架中学习的。
[125] 解耦了在 VAE 中学习到的细粒度域信息和类别信息。
[40] 还使用 VAE 进行解耦，他们提出了统一特征解耦网络 (UFDN)，将感兴趣的数据域和图像属性视为要解耦的潜在因素。
[126] 解耦了样本的语义和变分部分。类似的精神还包括 [130, 129]。
[127] 提出使用生成模型来解耦风格和其他信息，他们的方法既适用于域适应又适用于域泛化。

生成模型不仅可以提高 OOD 性能，还可以用于生成任务，我们认为这对许多潜在的应用程序很有用。

4.2.2.3 Causality-inspired methods

因果关系启发方法：因果关系是对统计之外的变量关系（联合分布）的更精细描述。因果关系提供了系统在干预下将如何表现的信息，因此它自然适用于迁移学习任务，因为域迁移可以被视为一种干预。特别是，在因果考虑下，期望的表示是标签的真正原因（例如，对象形状），因此预测不会受到对相关但语义上不相关的特征（例如，背景、颜色、样式）的干预的影响。有许多作品 [202, 203, 204, 205] 利用因果关系进行域适应。

对于域泛化，

[136] 以某种方式重新加权输入样本，以使加权相关性反映因果效应。
[134] 将傅里叶特征作为图像的成因，并强制这些特征之间的独立性。
使用对象身份（object identity）的附加数据（它是一个比类标签更详细的标签），[206] 强制表示在给定相同对象的域索引中的条件独立性。
当这样的对象标签不可用时，[76] 在单独的阶段进一步学习基于标签的对象特征。
对于单源域泛化，[107, 135] 使用数据增强来呈现因果因素的信息。增强操作被视为在对不相关特征的干预下产生结果，这是基于特定领域知识实现的。在因果考虑下也有生成方法。
[131] 显式地建模了一个导致域偏移的操作变量，这可能是未被观察到的。
[132] 利用因果不变性进行单源泛化，即基于因素生成（x，y）数据的过程的不变性，这比现有方法隐含依赖的推理不变性更普遍。这两个因素是允许相关的，这是更现实的。他们从理论上证明了因果因素的可识别性是可能的，并且识别有利于泛化。
[133] 将该方法和理论扩展到多个源域。有了更多的信息数据，不相关的因素也可以识别。

4.3 Learning Strategy

除了数据操作和表示学习，DG还在通用机器学习范式中进行了研究，分为几类：基于集成学习的DG、基于元学习的DG、基于梯度操作的DG、基于分布鲁棒优化的DG DG、基于自我监督学习的 DG 和其他策略。

4.3.1 Ensemble learning-based DG

集成学习通常结合多个模型，例如分类器或专家，以增强模型的威力。对于域泛化，集成学习通过使用特定的网络架构设计和训练策略来利用多个源域之间的关系来改进泛化。他们假设任何样本都可以看作是多个源域的集成样本，因此整体预测结果可以看作是多个域网络的叠加。

[139] 提出使用可学习的权重来聚合来自不同源特定分类器的预测，其中域预测器用于预测样本属于每个域的概率（权重）。
[69] 为不同的源域维护了依赖于域的批归一化 (BN) 统计数据和 BN 参数，而所有其他参数都是共享的。在推理中，最终预测是域相关模型与通过测量测试样本的实例归一化统计数据与每个域的累积总体统计数据之间的距离推断的组合权重的线性组合。
[137] 的工作提出了不同源域的特定域层，并学习这些层的线性聚合来表示测试样本。
[8] 提出了域自适应集成学习 (DAEL)，其中 DAEL 模型由跨域共享的 CNN 特征提取器和多个特定于域的分类器头组成。每个分类器都是其自己领域的专家，而不是其他领域的专家。 DAEL 旨在通过与专家一起教授非专家来协作学习这些专家，以鼓励整体学习如何处理来自未知领域的数据。还有其他作品 [138, 142]。

集成学习仍然是 DG 的强大工具，因为集成允许更多样化的模型和特征。然而，基于集成学习的 DG 的一个缺点可能是它的计算资源，因为我们需要更多的空间和计算来训练和保存不同的模型。

4.3.2 Meta-learning-based DG

元学习的关键思想是通过基于优化的方法 [207]、基于度量的学习 [208] 或基于模型的方法 [209] 从多个任务中学习通用模型。元学习的思想已被用于域泛化。他们将来自多源域的数据划分为元训练集和元测试集以模拟域转移。表示要学习的模型参数，元学习可以表示为：
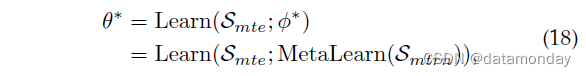
在这里插入图片描述
其中 φ∗ = MetaLearn(Smtrn) 表示来自元训练集 Smtrn 的元学习参数，然后用于学习元测试集 Smte 上的模型参数 θ∗。两个函数 Learn(·) 和 MetaLearn(·) 是由不同的元学习算法设计和实现的，对应一个双层优化问题。梯度更新可以表示为：
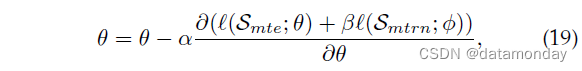
在这里插入图片描述
其中 η 和 β 分别是外循环和内循环的学习率。

[207] 提出了与模型无关的元学习（MAML）。受 MAML 的启发，[17] 提出 MLDG（用于域泛化的元学习）将元学习策略用于 DG。MLDG 将源域中的数据拆分为元训练和元测试，以模拟域迁移情况以学习一般表示。
[18] 提出为分类器学习元正则化器（MetaReg）。 [19] 通过设计元优化器为特征提取器提出了特征批评训练。
[143] 使用了类似的 MLDG 思想，并另外引入了两个互补损失来明确地规范特征空间的语义结构。
[20] 提出了一种扩展版本的信息瓶颈，称为元变分信息瓶颈（MetaVIB）。他们规范了来自不同领域的具有相同类别的样本的潜在编码分布之间的 Kullback-Leibler (KL) 分歧，并学习使用随机神经网络生成权重。最近，一些作品还对半监督 DG 或判别 DG [144, 145, 147, 44, 210] 采用了元学习。元学习在 DG 研究中被广泛采用，它可以被整合到几种范式中，例如解耦 [198]。

元学习在海量领域表现良好，因为元学习可以从多个任务中寻找可迁移的知识。

4.3.3 Gradient operation-based DG

除了元学习和集成学习，最近的几项工作考虑使用梯度信息来强制网络学习广义表示。[150] 提出了一种自挑战（self-challenging）的训练算法，旨在通过操纵梯度来学习一般表示。他们迭代地丢弃在训练数据上激活的主要特征，并强制网络激活与标签相关的剩余特征。这样，网络可以被迫从更多的坏案例中学习，从而提高泛化能力。[151] 提出了一种梯度匹配方案，他们的假设是两个域的梯度方向应该相同，以增强共同的表示学习。为此，他们提出最大化梯度内积（GIP）以对齐跨域的梯度方向。通过此操作，网络可以找到权重，以使输入-输出对应关系在跨域中尽可能接近。 GIP 可以表述为：
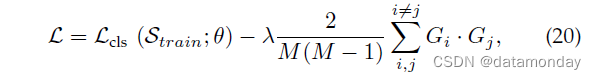
在这里插入图片描述
其中 Gi 和 Gj 是两个域的梯度，可以计算为 G = E ∂’(x,y;θ) ∂θ 。梯度不变性是通过在 [152] 中的梯度之间添加 CORAL [192] 损失来实现的，而 [153] 通过原始样本和增强样本之间的梯度相似性正则化来最大化 DNN 的神经元覆盖率。

4.3.4 Distributionally robust optimization-based DG

分布鲁棒优化 (distributionally robust optimization，DRO) [211] 的目标是在最坏的分布情况下学习一个模型，以希望它能够很好地泛化到与 DG 具有相似目标的测试数据。

为了优化最坏情况的分布情况，[212] 提出了一种 GroupDRO 算法，该算法需要对样本进行显式组注释。
这种注释后来被缩小到 [154] 中验证集的一小部分，他们制定了一个两阶段加权框架。
其他研究人员通过风险外推法 (risk extrapolation，VRex) [106] 或减少类条件 Wasserstein DRO [157] 来降低训练域风险的方差。
最近，[156] 提出了亚群迁移（subpopulation shift）的设置，他们也将 DRO 应用于这个问题。特别是，[79] 提出了 AdaRNN，一种类似于 DRO 精神的算法，不需要显式的组注释；相反，他们通过解决优化问题来了解最坏情况的分布情况。

总而言之，DRO 专注于也可用于 DG 研究的优化过程。

4.3.5 Self-supervised learning-based DG

自监督学习 (SSL) 是一种最近流行的学习范式，它从大规模未标记数据中构建自监督任务 [213]。

受此启发，[158] 引入了解决拼图游戏的自我监督任务，以学习广义表示。除了引入新的借口任务外，对比学习是另一种流行的自我监督学习范式，最近的几项工作都采用了这种范式[159,161,160]。对比学习的核心是在正负对之间进行无监督学习。
请注意，自监督学习是一种通用范式，可以应用于任何现有的 DG 方法，尤其是在训练域中没有标签的无监督 DG [80]。基于 SSL 的 DG 的另一个可能应用是多域数据的预训练，它可以训练强大的预训练模型，同时还可以处理域迁移。

然而，基于 SSL 的 DG 可能存在的限制可能是其计算效率和对计算资源的要求。

4.3.6 Other learning strategy for DG

还有一些其他的域泛化学习策略。例如，

[166] 中采用了度量学习来探索 DG 的更好的成对距离。
[162]使用随机森林来提高卷积神经网络（CNN）的泛化能力。他们根据随机森林给出的分割结果的概率质量函数对三元组进行采样，用于通过三元组损失更新 CNN 参数。
其他作品 [214, 215] 采用了 DG 的模型校准，他们认为校准后的性能与 OOD 性能密切相关。
[164] 遵循彩票假设为 DG 设计网络子结构。
[163] 专注于形状不变的特征。
[165] 观察到平坦最小值对 DG 很重要，他们设计了一种简单的随机权重平均密集方法来找到平坦最小值。

由于DG是一个通用的学习问题，未来会有更多使用其他策略的作品。

5 OTHER DOMAIN GENERALIZATION RESEARCH AREAS

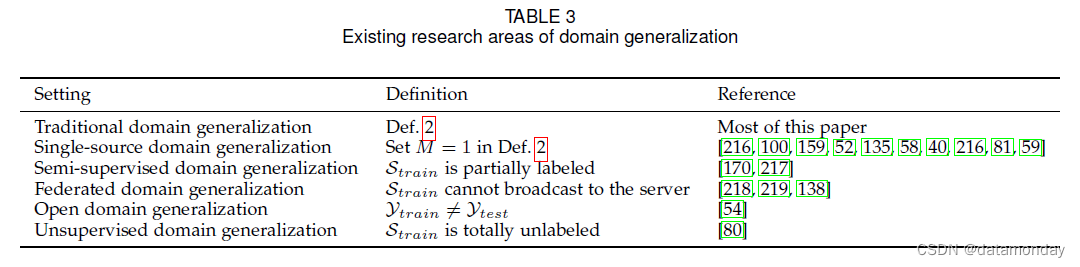
大多数现有的关于域泛化的文献都采用了 Def.2 中 DG 的基本（传统）定义。有一些现有文献将这种设置扩展到新场景以推动 DG 的前沿（参考表 3）。本节简要讨论现有的 DG 研究领域，让读者对这个问题有一个简要的概述。
在这里插入图片描述

5.1 Single-source Domain Generalization

在 Def.2 中设置 M = 1。给出单源 DG。与传统的 DG (M > 1) 相比，单源 DG 变得更具挑战性，因为训练领域的多样性较少。因此，这个问题的关键是使用数据生成技术生成新的域，以增加训练数据的多样性和信息量。几种方法为计算机视觉任务中的单源 DG 设计了不同的生成策略 [216, 100, 159, 52, 135, 58, 40, 81, 59]。最近的一项工作 [79] 在时间序列数据中研究了这种设置，其中通常有一个统一的数据集，通过使用最小-最大优化。我们预计更多的应用领域可以从单一来源的 DG 中受益。

5.2 Semi-supervised Domain Generalization

与传统的 DG 相比，半监督 DG 不需要训练域的完整标签。通常应用现有的半监督学习算法，如 FixMatch [220] 和 FlexMatch [221] 来学习未标记样本的伪标签。例如，最近的两项工作采用了半监督学习中的一致性正则化 [170, 217] 用于半监督 DG。可以看出，这个设定比传统的DG更笼统，我们期待这方面的作品会更多。

5.3 Federated Learning with Domain Generalization

机器学习的隐私和安全变得越来越重要 [222]。[223]首先研究了这个问题，并表明如果特征是稳定的，那么该模型对成员推理攻击的鲁棒性更强。在联邦 DG [224, 225] 中，模型不访问原始训练数据；相反，它们聚合来自不同客户端的参数。在这种情况下，关键是通过泛化技术设计更好的聚合方案[218,219,138]。联合 DG 在医疗保健中更为重要 [226]。另一方面，分散训练是另一种可能的解决方案[227]。但是，当需要更新模型时，会出现类似的隐私风险。因此，我们希望有更多的研究。

5.4 Other DG Settings

DG 中还有其他设置，例如开放域泛化（open domain generalization）[54] 和无监督域泛化 [80]。 Open DG 共享类似的通用域适应设置，其中训练和测试标签空间不相同。无监督 DG 假设训练域中的所有标签都不可访问。随着环境变得更加普遍和具有挑战性，将会有其他 DG 研究领域旨在解决某些限制。

6 APPLICATIONS

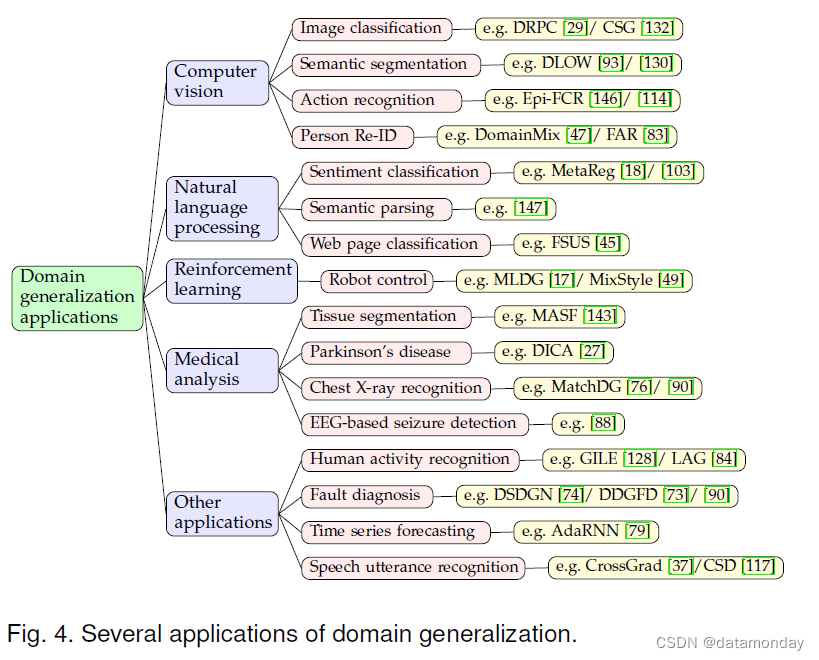
在这里插入图片描述
在本节中，我们将讨论域泛化的流行任务/应用程序（参考图 4）。

在各种视觉任务中都需要高泛化能力。许多作品在分类上研究 DG。

一些工作还研究了用于语义分割 [93]、动作识别 [114、146]、人脸反欺骗 [95]、ReID [47、83]、街景识别 [40]、视频理解 [116] 和图像压缩[228]。
医学分析 [120] 是 DG 的重要应用领域之一，因为它具有数据稀缺性和存在域差距的性质，具有组织分割 [143]、帕金森病识别 [27]、活动识别 [65]、胸部 X 射线识别 [76, 90] 和基于 EEG 的癫痫发作检测 [88]。
除了这些领域，DG 在机器人控制 [49, 17] 的强化学习中也很有用，以推广到看不见的环境。
一些工作使用 DG 来识别语音 [37、117]、故障诊断 [90、74、73]、物理学 [89]、脑机接口 [86]。

在自然语言处理中，训练数据来自具有不同分布的不同领域也是很常见的，而 DG 技术很有帮助。

一些工作在亚马逊评论数据集 [103, 18] 上使用域泛化来进行情感分类。
其他人使用 DG 进行语义解析 [147]、网页分类 [45]。
例如，如果得到来自多个领域的自然语言数据，并且想要学习一个能够很好地预测任何新域的泛化模型，可以使用域泛化来获取领域不变的表示。

此外，DG 技术在金融分析、天气预报、物流等一些应用领域具有广阔的前景。

[79] 尝试将 DG 用于时间序列建模。他们首先提出了广泛存在于时间序列数据中的时间协变量偏移问题，然后，他们提出了一种基于 RNN 的模型来解决这个问题，以对齐来自不同域的任意一对训练数据之间的隐藏表示。他们的算法，即所谓的 AdaRNN，被应用于股票价格预测、天气预报和电力消耗。
另一个例子是[128]，他们将域泛化应用于基于传感器的人类活动识别。在他们的应用程序中，来自不同人的活动数据来自不同的分布，当应用于新用户时会导致严重的模型崩溃。为了解决这个问题，他们开发了一种基于变分自编码器的网络来学习域不变和域特定的模块，从而实现解耦。

未来，我们希望可以在其他领域有更多的分布式发电应用，以应对广泛存在于不同应用中的分布转变。另一个重要问题是在不访问现实测试分布的情况下评估 DG 算法。虽然我们可以在研究中使用测试数据进行评估，但我们根本无法将其用于实际应用。在这种情况下，一种可能的方法是多次对原始数据执行元训练和元测试拆分。在每一次中，一个分割可以看作是看不见的测试数据，而另一个作为训练数据。我们可以将其称为现实中 DG 的元交叉验证。同时，我们也希望能有更多的评价指标。有关研究中的更多评估，请参阅下一节。

7 DATASETS, EVALUATION, AND BENCHMARK

在本节中，我们总结了现有的通用数据集和用于域泛化的模型选择策略。然后，我们介绍了代码库 DeepDG，并展示了通过它进行的实验的一些观察结果。

7.1 Datasets

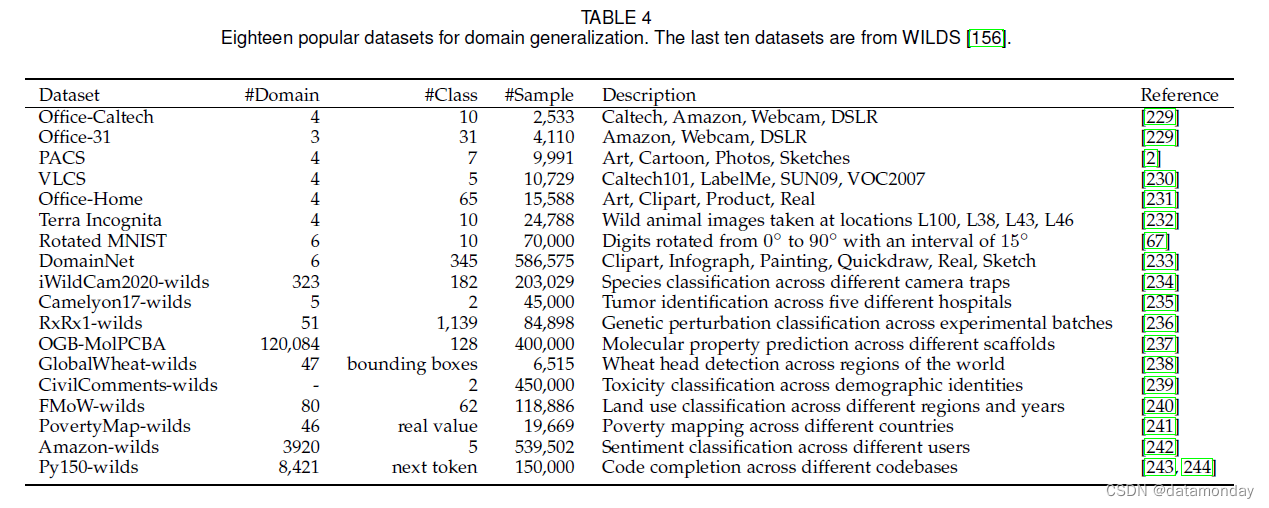
在这里插入图片描述
表 4 提供了几个流行数据集的概述。其中，PACS [2]、VLCS [230] 和 Office-Home [231] 是三个最受欢迎的数据集。对于大规模评估，DomainNet [233] 和 Wilds [156]（即表 4 中以“-wilds”结尾的数据集的集合）正变得越来越流行。

除了上面提到的数据集，还有一些其他的用于不同任务的域泛化数据集。移植物抗宿主病 (GvHD) 数据集 [245] 也很流行，用于测试流式细胞术问题的几种方法 [27, 6]。该数据集是从 30 名患者中收集的，样本量从 1,000 到 10,000 不等。这是一个时间序列分类数据集。一些作品 [93, 29, 71] 将域泛化应用于语义分割，其中 CityScape [246] 和 GTA5 [247] 数据集被用作基准数据集。一些作品将 DG 应用于对象检测，使用 Cityscapes [246]、GTA5 [247]、Synthia [248] 的数据集进行调查 [71]。其他一些作品使用公共数据集或 RandPerson [249] 进行人员重新识别 [186、250、70]。一些作品 [17, 49] 使用 OpenAI Gym [251] 作为测试平台来评估算法在诸如 Cart-Pole 和山地车等强化学习问题中的性能。

除了这些广泛使用的数据集外，现有文献中还使用了其他数据集。帕金森远程监测数据集 [252] 很受欢迎，用于预测临床医生的运动和通过语音测量对帕金森病症状的总 UPDRS 评分。一些方法 [27, 60, 61] 使用来自几个人的数据作为训练域来学习泛化到看不见的主题的模型。

值得注意的是，域泛化的数据集与域适应有一些重叠。例如，Office-31、Office-Caltech、Office-Home 和 DomainNet 也是广泛使用的域适应基准。因此，除了我们这里讨论的那些之外，大多数域适应数据集都可以用于域泛化基准测试。例如，Amazon Review 数据集 [253] 广泛用于域适应。它在产品评论上有四个不同的领域（DVD、厨房电器、电子产品和书籍），它们也可以用于领域泛化。

7.2 Evaluation

为了在测试域上测试域泛化算法，提出了三种策略[87]，即

测试域验证集：测试域验证集利用部分目标域作为验证。尽管它在大多数情况下都能获得最佳性能，因为验证和测试共享相同的分布，但在训练时往往无法访问目标，这意味着它无法在实际应用中采用。
留一个域交叉验证：当训练数据包含多个来源时，保留一个域是另一种选择最终模型的策略。它将一个训练源作为验证，而将其他训练源作为训练部分。显然，当训练数据中只存在单一来源时，它不再适用。
训练域验证集：由于源和目标之间的分布不同，最终结果严重依赖验证的选择，这使得最终结果不稳定。域泛化最常见的策略是在大多数现有工作中使用的训练域验证集。在这个策略中，每个源都分为两部分，训练部分和验证部分。将所有训练部分组合起来进行训练，而将所有验证部分组合起来以选择最佳模型。由于组合验证与真正看不见的目标之间仍然存在差异，因此这种简单且最流行的策略在一段时间内无法达到最佳性能。

我们需要提到的是，DG 或 OOD 可能存在其他评估协议，例如 [167]，因为设计有效的评估协议通常与 OOD 性能一致。目前，大多数工作采用训练域验证策略，由于验证集的分布与新的训练数据不同，因此可能并不总是产生良好的性能。另一方面，仅使用准确性可能不足以验证模型性能。我们期待新的评估指标能够尽可能真实地反映属性测试分布，以获得更好的结果。

7.3 Benchmark

为了在统一的代码库中测试 DG 算法的性能，在本文中，我们为 DG 开发了一个新的代码库，名为 DeepDG [254, 255]。与现有的 DomainBed [87] 相比，DeepDG 简化了数据加载和模型选择过程，同时还可以在单台机器上运行所有实验。 DeepDG将整个过程拆分为数据准备部分、模型部分、核心算法部分、程序入口和其他一些辅助函数。每个部分都可以由用户自由修改而不影响其他部分。用户可以将自己的算法或数据集添加到 DeepDG 中，并公平地与一些最先进的方法进行比较。DeepDG 当前的公共版本仅用于图像分类，我们提供对 Office-31、PACS、VLCS 和 Office-Home 数据集的支持。目前，在同一环境下实现了九种最先进的方法，它涵盖了所有三个组，包括数据操作（Mixup [173]）、表示学习（DDC [188]、DANN [91]、CORAL [ 191]）和学习策略（MLDG [17]、RSC [150]、GroupDRO [155]、ANDMask [256]）。
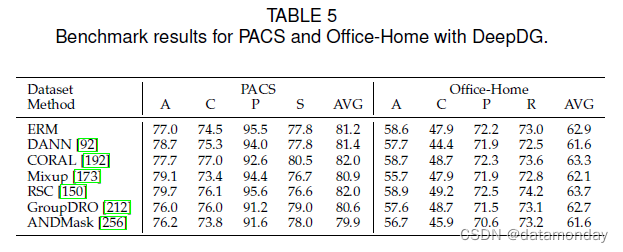
在这里插入图片描述
我们对两个最流行的图像分类数据集 PACS 和 Office-Home 进行了一些实验，其中 DeepDG 和表 5 显示了结果。 ResNet-18 用作基础特征网络。训练域验证集用于选择最终模型，20% 的源用于验证，其他用于训练。从表 5 中，我们观察到更深刻的结论。

(1) 基线方法 ERM 在两个数据集上都取得了可接受的结果。一些方法，例如 DANN 和 ANDMask，性能甚至更差。

(2) 简单的数据增强方法，Mixup，不能取得显着的效果。

(3) 与 ERM 相比，CORAL 在两个数据集上都有轻微的改进，这与 DomainBed [87] 提供的结果一致。

(4) RSC 是一种学习策略，在两个数据集上都取得了最好的性能，但与 ERM 相比，改进并不显著。结果表明域泛化在不同任务中的好处。

8 DISCUSSION

在本节中，我们总结了现有的方法，然后提出了在未来研究中值得关注的几个挑战。

8.1 Summary of Existing Literature

训练数据的数量和多样性对模型的泛化能力非常重要。许多方法旨在使用上述数据操作方法来丰富训练数据以实现良好的性能。然而，数据操作方法的一个问题是缺乏对泛化的无限风险的理论保证。因此，重要的是开发基于操作的方法的理论，以便在不违反道德标准的情况下进一步指导数据生成设计。

与数据操作相比，表示学习通常具有理论支持[179,6,102]。基于内核的方法在传统方法中得到了广泛的应用，而基于深度学习的方法近年来发挥了主导作用。虽然域对抗训练通常在域适应方面取得更好的性能，但在 DG 中，我们没有看到这些对抗方法的显着结果改进。我们认为这可能是因为任务相对容易。对于显式分布匹配，越来越多的工作倾向于匹配联合分布，而不仅仅是匹配边缘 [6, 72] 或条件 [63] 分布。因此，执行动态分布匹配更可行[189, 190]。解耦和 IRM 方法都具有良好的泛化动机，同时可以开发更有效的训练策略。有几项研究[257]指出仅仅学习域不变特征是不够的，还应该考虑表示平滑度。

对于学习策略，有一种趋势是许多作品将元学习用于 DG，这需要设计更好的优化策略来利用不同领域的丰富信息。除了深度网络，还有一些工作 [162] 将随机森林用于 DG，我们希望能有更多多样化的方法出现。

8.2 Future Research Challenges

我们总结了 DG 未来的一些研究挑战。

8.2.1 Continuous domain generalization

对于许多实际应用程序，系统使用具有非平稳统计信息的流数据。在这种情况下，执行有效更新 DG 模型，以克服灾难性遗忘，并适应新数据的连续域泛化非常重要。虽然有一些专注于持续学习的领域适应方法[258]，但在实际场景中有利的情况下，对连续 DG [259] 的研究很少。

8.2.2 Domain generalization to novel categories

现有的 DG 算法通常假设不同域的标签空间是相同的。更实用和通用的设置是支持对新类别的泛化，即域泛化和任务泛化。这在概念上类似于元学习和零样本学习的目标。一些工作 [85, 260] 提出了零样本 DG，我们预计该领域会有更多工作。有一些先前的工作 [54, 261] 试图使用基于边界的学习范式或一致性正则化来解决这个问题，这些都是未来工作可能会在它们之上构建方法的好方法。

8.2.3 Interpretable domain generalization

基于解耦的 DG 方法将特征分解为域不变/共享和域特定部分，这为 DG 提供了一些解释。对于其他类别的方法，仍然缺乏对 DG 模型中学习特征的语义或特征的深入理解。例如，如何将方法的结果与输入特征空间相关联。当前提供这种可解释性水平的方法有多接近？因果关系[132]可能是理解域泛化网络并提供解释的一种有前途的工具。

8.2.4 Large-scale pre-training/self-learning and DG

近年来，我们见证了大规模预训练/自学习的快速发展，例如 BERT [262]、GPT-3 [263] 和 Wav2vec [264]。对大规模数据集进行预训练，然后将模型微调到下游任务可以提高其性能，其中预训练有利于学习一般表示。因此，如何设计有用且高效的 DG 方法来帮助大规模预训练/自学习是值得研究的。

8.2.5 Test-time Generalization

虽然 DG 专注于训练阶段，但我们也可以在推理阶段请求测试时泛化。这进一步连接了域适应和域泛化，因为我们还可以使用推理未标记数据进行适应。最近很少有作品 [265, 266] 关注此设置。与传统的 DG 相比，测试时泛化将在推理时间上提供更大的灵活性，同时它需要更少的计算和更高的效率，因为推理端设备中的资源通常是有限的。

8.2.6 Performance evaluation for DG

最近的工作 [87] 指出，在几个数据集上，一些 DG 方法的性能几乎与基线方法相同（即经验风险最小化）。我们不认为这是 DG 在实际应用中没有用的充分证据。相反，我们认为这可能是由于今天使用的评估方案不合适，或者域差距没有那么大。在更现实的情况下，例如存在明显领域差距的人 ReID [71]，DG 的改进是显着的。因此，我们对 DG 的价值保持乐观，并希望研究人员也能找到更适合研究的设置和数据集。

9 CONCLUSION

泛化一直是机器学习研究中的一个重要研究课题。在本文中，我们通过对理论、现有方法、数据集、基准和应用程序的深入分析来回顾领域泛化领域。然后，我们彻底分析这些方法。根据我们的分析，我们提供了几个潜在的研究挑战，这些挑战可能是未来研究的方向。我们希望这项调查能够为研究人员提供有用的见解，并在未来激发更多的进步。