---

前言

🐱个人主页： 代码探秘者
🐭C语言专栏：C语言
🐰C++专栏： C++ / STL使用以及模拟实现/C++11新特性
🐹数据结构专栏： 数据结构 / 十大排序算法
🐶 Linux专栏： Linux系统编程 / Linux网络编程（准备更新）
🌈喜欢的诗句:天行健,君子以自强不息.

---

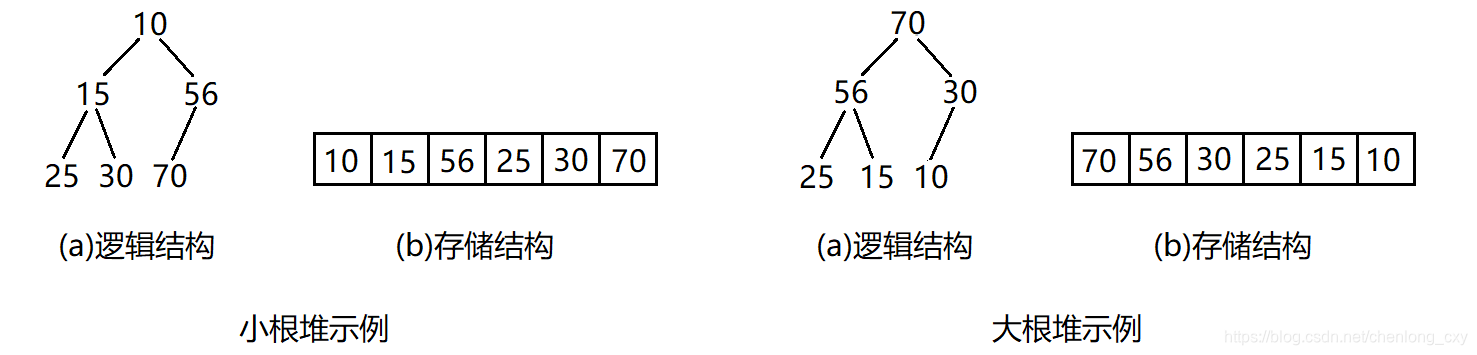
堆的定义

1.大小堆

堆（英语：heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

小堆：将根结点最小的堆叫做小堆，也叫最小堆或小根堆。
大堆：将根结点最大的堆叫做大堆，也叫最大堆或大根堆。

2.完全二叉树

1、完全二叉树：若二叉树的深度为h，则除第h层外，其他层的结点全部达到最大值，且第h层的所有结点都集中在左子树。

2、满二叉树：满二叉树是一种特殊的的完全二叉树，所有层的结点都是最大值。

堆的实现

堆的数据结构

typedef int DataType;
typedef struct Heap
{DataType* a;int size;		//当前堆大小int capacity;	//容量
}HP;

初始化

void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}

销毁

//销毁
void HPDestory(HP* hp)
{if (hp->a){free(hp->a);hp->size = hp->capacity = 0;}
}

取堆顶元素

//返回堆顶元素
DataType HPTop(HP* hp)
{assert(hp);assert(!HPEmpty(hp));	//堆不为空return hp->a[0];
}

判断堆是否为空

//判断是否为空
bool HPEmpty(HP* hp)
{assert(hp);return hp->size == 0;
}

父结点和子结点下标关系（重要）

注意：在二叉树中，我们本文默认根结点下标为0，若当前节点的下标为 i，

• 其父节点的下标为 i/2
• 其左子节点的下标为 i*2
• 其右子节点的下标为i*2+1

当然也有人选择根结点下标为1

向下调整法-O(n)

• 向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

小堆版

我们通过从根结点开始的向下调整算法可以把它调整成一个小堆。

• 向下调整算法有一个前提：左右子树必须是一个小堆，才能调整。
• 选出最小的左右孩子
• 最小孩子比父亲小，就交换上来
• 更新parent和minchild，一直循环到最后

int array[] = {27,15,19,18,28,34,65,49,25,37};

//向下调整:从哪里开始
//删除调用
void AdjustDown(DataType* a, int n, int parent)
{//先找到最小的孩子int minchild = 2 * parent + 1;	//假设左孩子最小while (minchild < n){//右孩子存在，而且小于左孩子if (minchild + 1 < n && a[minchild + 1] < a[minchild]){minchild++;		//更新最小为右孩子}//开始向下调整//小堆为例)if (a[minchild] < a[parent]){Swap(&a[minchild], &a[parent]);	//交换//更新parent和minchildparent = minchild;minchild = 2 * parent + 1;}else{break;}}
}

大堆版

就是变化一点而已
这里向下调整算法有一个前提：左右子树必须是一个大堆，才能调整。

• 选出最大的孩子
• 最大孩子比父亲大，就交换上来
• 更新parent和minchild，一直循环到最后

//向下调整:							从哪里开始
//删除调用
void AdjustDown(DataType* a, int n, int parent)
{//先找到最大的孩子int maxchild = 2 * parent + 1;	//假设左孩子最小while (maxchild < n){//右孩子存在，而且大于左孩子if (maxchild + 1 < n && a[maxchild+ 1] > a[maxchild]){maxchild++;		//更新最大为右孩子}//开始向下调整//大堆为例if (a[maxchild] > a[parent]){Swap(&a[maxchild], &a[parent]);	//交换//更新parent和minchildparent = maxchild;maxchild = 2 * parent + 1;}else{break;}}
}

向上调整法-nlog(n)

当我们在一个堆的末尾插入一个数据后，需要对堆进行调整，使其仍然是一个堆，这时需要用到堆的向上调整算法。

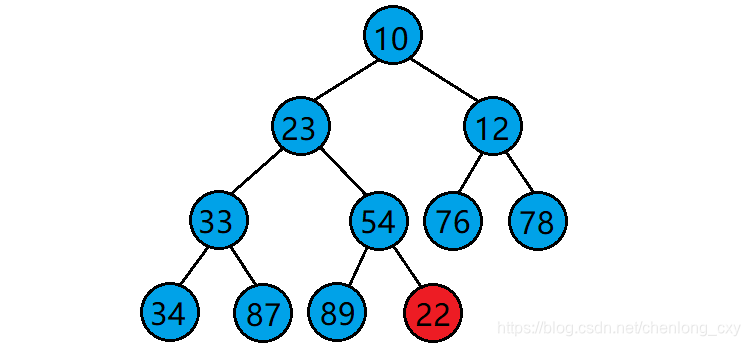
向上调整算法的基本思想（以建小堆为例）：
 1.将目标结点与其父结点比较。
 2.若目标结点的值比其父结点的值小，则交换目标结点与其父结点的位置，并将原目标结点的父结点当作新的目标结点继续进行向上调整。若目标结点的值比其父结点的值大，则停止向上调整，此时该树已经是小堆了。

堆的插入和删除

插入(调用向上调整)

• 当然要考虑扩容的问题

• 每次插入都是将先将新数据放在数组最后

• 如果堆的性质破坏，就从插入新节点进行向上调整

//入堆(保持插入后还是堆)
void HPPush(HP* hp, DataType a)
{assert(hp);//容量不足:扩容if (hp->capacity == hp->size){size_t newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;DataType* tmp = (DataType*)realloc(hp->a,sizeof(DataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}hp->a = tmp;		//赋值弄回来hp->capacity = newcapacity;//新空间}hp->a[hp->size] = a;hp->size++;//从刚刚插入的结点位置，进行向上调整AdjustUp(hp->a, hp->size - 1);	//减-1，因为刚刚+1
}

删除(调用向下调整)

删除堆是删除堆顶的数据

• 将堆顶的数据根最后一个数据一换
• 然后删除数组最后一个数据
• 再从根结点进行向下调整算法。
  

//出堆
void HPPop(HP* hp)
{assert(hp);assert(!HPEmpty(hp));	//堆不为空//交换：堆顶元素移动最后面Swap(&hp->a[0],&hp->a[hp->size-1]);hp->size--;		//把最后一个元素删掉，元素个数减1//然后从根节点进行向下调整AdjustDown(hp->a,hp->size,0);}

构建最大堆

怎么建堆？

常用的方法：直接插入法和向下调整（堆化）

向上调整-直接插入法

直接插入法：这种方法通过逐个插入元素，每次插入后进行向上或向下调整，直到整个数组满足堆的性质。虽然时间复杂度为O(nlogn)，但它简单直观，适用于元素数量不多的情况。

//建堆
void testHeap1()
{int a[] = { 50,100,70,65,60,32 };HP hp;int n = sizeof(a) / sizeof(a[0]);//插入法建堆-向上调建堆N*logNfor (int i = 1; i < n; i++){HPPush(&hp,a[i]);		//调用插入}
}
int main()
{testHeap1();return 0;
}

向下调整法建堆（从最后一个非叶子节点开始）

• 自下而上，向下调整法建堆：从最后一个非叶子节点开始，即从数组的中间开始，直到根节点。

向下调整（堆化）：这是构建最大堆和最小堆最常用的方法。它从最后一个非叶子节点开始，逐个进行向下调整，直到根节点。这种方法的时间复杂度为O(n)，非常高效。

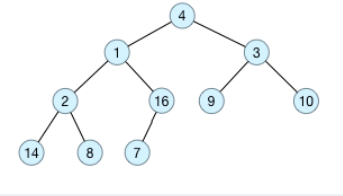
原始数据为a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}，采用顺序存储方式，对应的完全二叉树如下图所示：

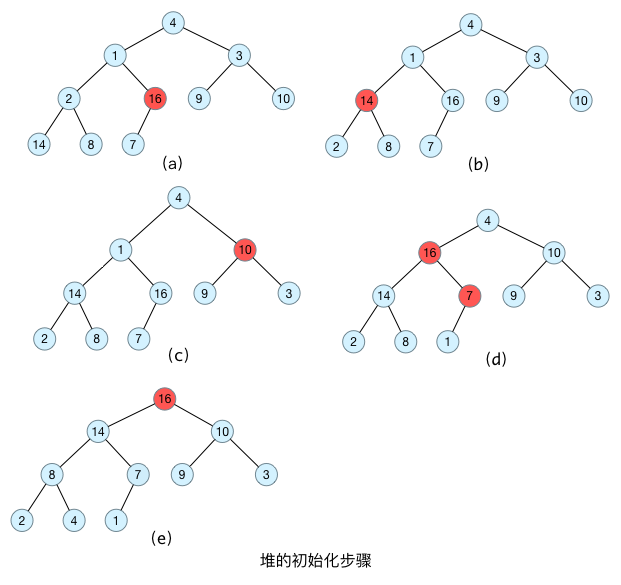
基本思想：
首先将每个叶子节点视为一个堆，再将每个叶子节点与其父节点一起构造成一个包含更多节点的对。

• 最后一个非叶子结点下标：(n - 1 - 1) / 2（从0开始编号）

• （a）在构造堆的时候，首先需要找到最后一个节点的父节点(就是最后一个非叶子结点)，最后一个节点为7，其父节点为16，从16这个节点开始构造最大堆；

• (b) 然后就继续16的上一个节点14，把这颗子树调整为大堆

• (c）(d) (e): 一直调整到根节点

代码实现如下：

//建堆
void testHeap1()
{int a[] = { 50,100,70,65,60,32 };int n = sizeof(a) / sizeof(a[0]);// 向下调整建堆 O(N)for (int i = (n-1-1)/2; i >= 0; i--){AdjustDown(a, n, i);}
}
int main()
{testHeap1();return 0;
}

构建最小堆

只需要简单调用上面代码，整体操作和最大堆类似，这里不做赘述

性能分析

时间复杂度

向上调整法（Insertion）
向上调整法是在堆中插入一个新元素时使用的。新元素被插入到堆的末尾，然后如果它比父节点大（在最大堆中）或小（在最小堆中），则需要向上移动，直到它不再违反堆的性质或者到达根节点。

时间复杂度：O(log n)

这是因为在最坏的情况下，新元素可能需要一直移动到根节点，而一个完全二叉树的高度是log n级别的。

如果我们使用向上调整法来逐个插入元素以构建堆，那么我们需要对数组中的每个元素执行一次插入操作，总共需要执行 n 次插入操作，因此总的时间复杂度将是 O(n log n)。

==向下调整法（Heapify）==的时间复杂度

向下调整法是在构建堆或者删除堆顶元素后，用于维护堆的性质。从根节点开始，如果根节点违反了堆的性质，就将它和子节点中最大的（在最大堆中）或最小的（在最小堆中）交换，然后对交换后的子树继续进行向下调整。

时间复杂度：O(log n)

这是因为在最坏的情况下，需要调整的节点可能一直到达叶子节点，而树的高度是log n级别的。

建堆的时间复杂度

建堆是指将一个无序的数组转换为一个堆结构。通常使用向下调整法（Heapify）来完成这个过程。

时间复杂度：O(n)

这个时间复杂度是基于这样一个事实：在构建堆的过程中，最后一个非叶子节点到根节点的向下调整操作的总时间复杂度是O(log n)，而这样的节点有n/2个（对于n个节点的数组）。因此，总的时间复杂度是O(n/2 * log n)，简化后为O(n)。

关键字对比

总结一下

堆的向下调整算法的时间复杂度：O(log n)
 
建堆的时间复杂度： O(n log n)

堆的向上调整算法的时间复杂度： O(log n)

建堆的时间复杂度： O(n)

堆排序

详细文章点这里

TOK问题

详细文章点这里