一.树

1.1树的概念与结构

树是一种非线性数据结构，由有限个结点组成的具有层次关系的集合。树的根部位置就叫根结点，除根结点以外，其余的树被分为各个互不相交的集合。树的根系只能向下延伸不能向左右延伸。除根结点以外每个结点有且仅有一个父结点。一棵n个结点的树有n-1条边。

1.2相关术语

父结点：若结点含有子节点那么必定是由父结点而来。

子结点：一个结点含有的子树的根结点称为该结点的子结点。

结点的度：一个结点她有多少孩子，他的度就是多少。

树的度：一棵树最大的结点的度称为树的度。

结点的层次：从根结点开始计算。

树的高度和深度：树结点中的最大层次。

二.二叉树

2.1概念与结构

二叉树是结点的一个有限集合。他的度不存在大于2的结点，子树有左右之分，次序不能颠倒，因此二叉树是有序树。

2.2特殊二叉树

一棵二叉树如果结点数达到最大值，则这个二叉树就是满二叉树。也就是说如果一个二叉树层数为k，那么结点个数为（2的k次方）-1。

完全二叉树是一个效率很高的数据结构，树的大小从左向右增大趋势，并且中间不能有空，结点之间紧挨着。具有n个结点的满二叉树深度h＝log2（n+1）。

三.实现顺序结构的二叉树

3.1堆的概念

按完全二叉树的顺序储存方式储存，在一个一维数组中满足ki＜＝k（2*i+1），根结点是最大值的堆叫大堆，根结点最小值的堆是小堆。

3.2二叉树的性质

若i＞0，i位置的父结点为（i-1）/2                              若2i+1＜n，左孩子的序号为2i+1，右孩子的序号为2i+2

3.3堆的实现

堆的底层结构为数组，因此堆的结构为：

 接下来需要实现的功能

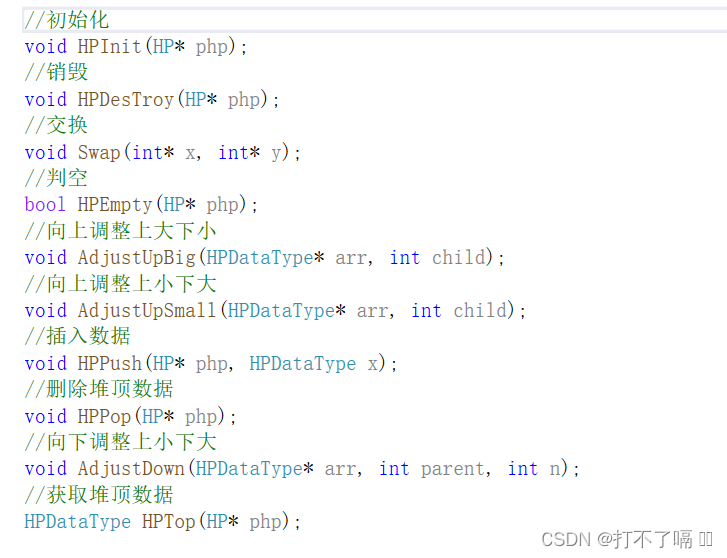
 四.堆的实现

4.1初始化和销毁

根据数据结构的变量来进行初始化，数组制为空，大小容量制为0。销毁时则相反。

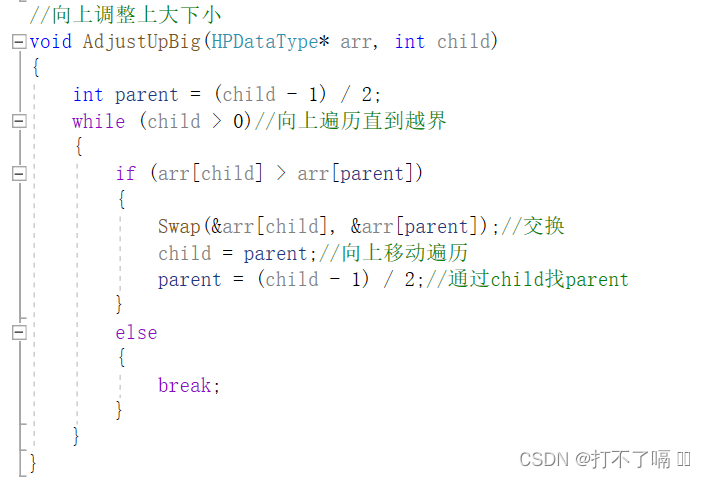
 4.2向上调整向下调整

假设我们取大堆，形参接收一个child结点，并找到parent结点，两者相互比较，若child大，则两节点互换值，child结点跑到parent结点，若child结点一直小，我们可以用while循环不断循环，直到child小于等于0截止。

 

 

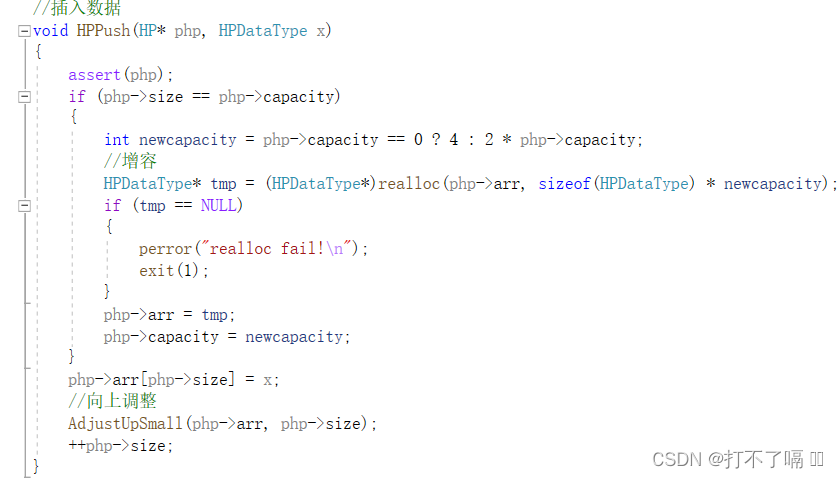
4.3插入数据

首先要明确，我们插入数据是在尾部插入数据。插入数据前要先判断capacity是否足够，若不够则开辟相应空间大小，接着在size处插入数据，向上调整形成小堆最后要++size。

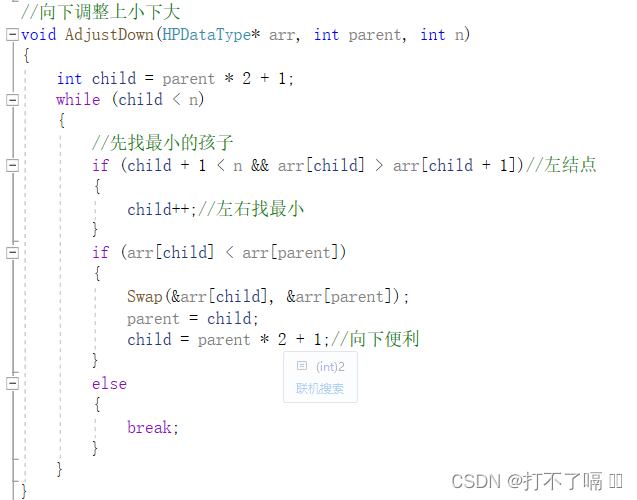
 4.4删除堆顶数据

因为堆顶在堆的头部，不能进行直接删除，所以我们可以将其与队尾互换值，删除队尾，在进行堆的调整。