目录
一、说明
二、固定时间间隔示例
三、固定间隔的示例
四、泊松分布的主要特征
五、示例
5.1 平均客户数的计算:
5.2 用于计算和绘制泊松分布的 Python 代码:

一、说明
泊松概率分布是一种离散概率分布,它表示在固定的时间或空间间隔内发生给定数量的事件的概率,前提是这些事件以已知的恒定平均速率发生,并且与自上次事件以来的时间无关。此分布对于对罕见事件进行建模特别有用。
泊松分布以生活在 58 年(1781-1840 年)的西蒙·丹尼斯·泊松男爵的名字命名。泊松是一位法国数学家和物理学家,以其在各个领域的广泛贡献而闻名,包括统计学、复分析、偏微分方程、变分微积分、分析力学、电和磁学、热力学、弹性和流体力学。
注: 固定的时间或空间间隔是指观察或测量事件的特定、不变的时间段或区域。以下是两者的示例:
二、固定时间间隔示例
- Number of Emails Received per hour (每小时接收的电子邮件数量):假设您要对客户服务部门在一小时内收到的电子邮件数量进行建模。此处,固定时间间隔为 1 小时。如果该部门平均每小时收到 10 封电子邮件,则泊松分布可用于预测在任何给定小时内收到不同数量电子邮件的概率。
三、固定间隔的示例
- 一公顷森林中的树木数量:假设您正在研究森林中特定树种的分布。您可能想知道在一公顷的土地上找到一定数量的这些树的概率。在这里,固定的空间间隔是 1 公顷。如果每公顷的平均树木数为 50,则泊松分布可以帮助对在任何给定公顷内找到不同数量的树木的可能性进行建模。
四、泊松分布的主要特征
- 参数:泊松分布由单个参数 λ (lambda) 定义,该参数表示指定区间内的平均事件数。
- 概率质量函数:在给定区间内观察到 k 个事件的概率计算如下:
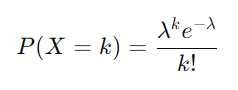
其中 k 是非负整数 (0, 1, 2, ...),e 是自然对数的底数(约为 2.71828)。
3. 均值和方差:在泊松分布中,均值和方差都等于 λ。

五、示例
假设我们有兴趣对早高峰时段每 10 分钟到达咖啡店的顾客数量进行建模。根据历史数据,我们观察到以下内容:

在此示例中,我们观察到了在三个 10 分钟间隔内到达的客户数量。此数据为我们提供了对每个间隔的平均客户数的见解。
5.1 平均客户数的计算:
为了找到每 10 分钟间隔的平均客户数 (λ),我们将每个间隔中观察到的客户数相加,然后除以间隔数:
- 客户总数 = 3 + 7 + 4 = 14
- 间隔数 = 3
- 每个区间的平均客户数 = 14/3 ≈ 4.67
10:30 AM 到 10:40 AM 间隔的预测:
为了预测上午 10:30 到上午 10:40 间隔的客户数量,我们将使用每 10 分钟间隔的平均客户数量,我们计算得出的顾客数量约为 4.67。
对于在上午 10:30 到 10:40 之间到达的每个可能数量的客户 k,我们将使用泊松分布公式:
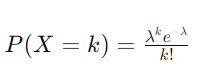
这里:
- k 是到达的客户数量 (0, 1, 2, ...)
- λ 是每 10 分钟间隔的平均客户到达率(约为 4.67)
- e 是自然对数的底数(约为 2.71828)。
5.2 用于计算和绘制泊松分布的 Python 代码:
import numpy as np
import matplotlib.pyplot as plt
import math# Define the rate parameter (lambda) for the Poisson distribution
lambda_ = 4.67# Define the range of possible number of customers (from 0 to 10)
x = np.arange(0, 11)# Calculate the probability mass function (PMF) for each number of customers
pmf = [math.exp(-lambda_) * (lambda_ ** k) / math.factorial(k) for k in x]# Plotting the Poisson distribution
plt.figure(figsize=(10, 6))
plt.bar(x, pmf, color='skyblue', edgecolor='black')
plt.title('Poisson Distribution: Number of Customers Arriving Between 10:30 AM and 10:40 AM')
plt.xlabel('Number of Customers')
plt.ylabel('Probability')
plt.xticks(x)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()这是上面的代码输出:
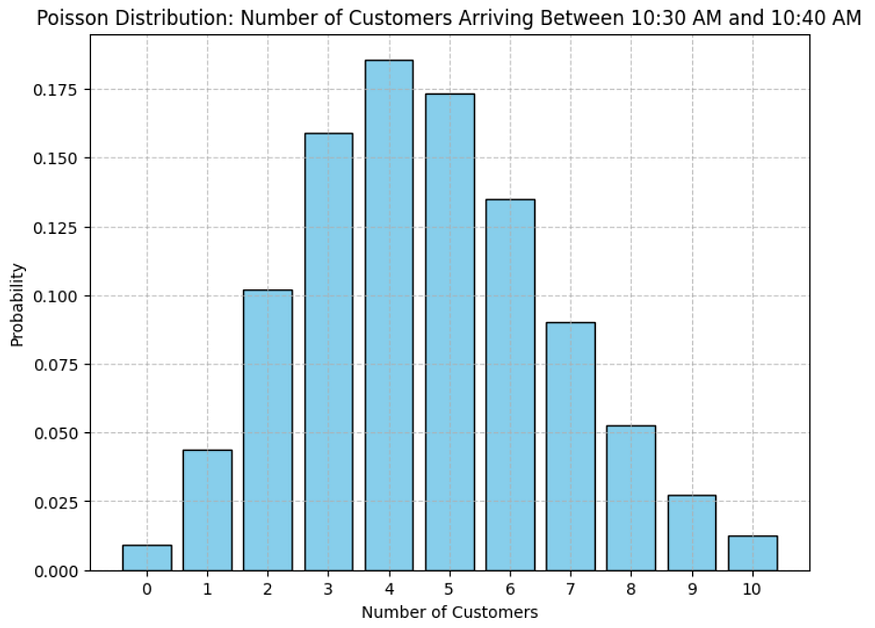
在 ML 系列的第 24 天,我们深入研究了泊松分布,而第 20 天到第 24 天则专门探索了各种著名的离散分布。



















