【机器学习】聚类算法原理详解

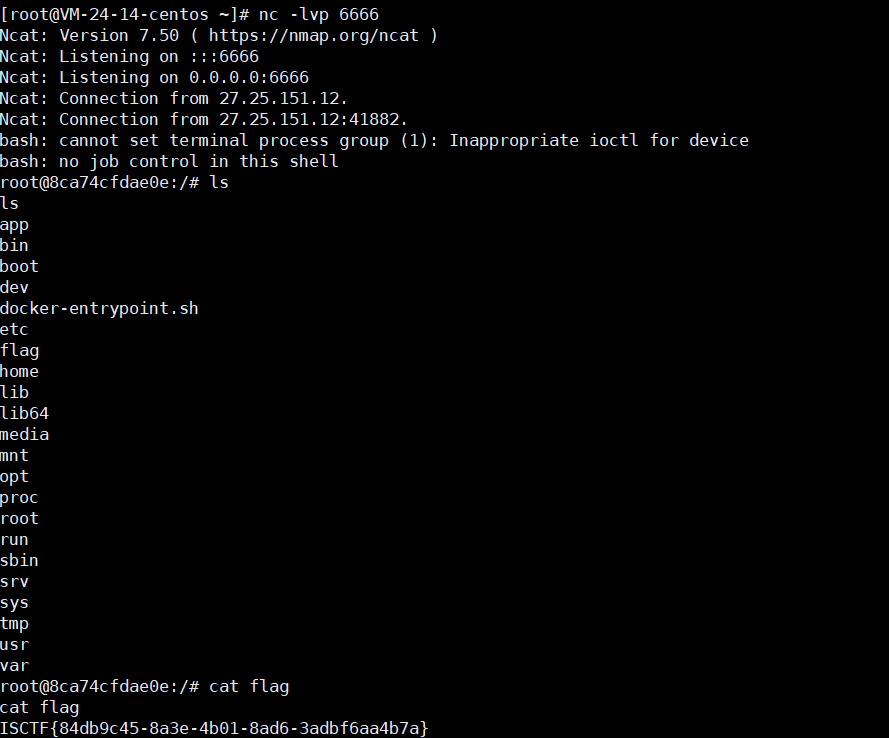
聚类算法

性能度量：

外部指标
- jaccard系数（简称JC）
- FM指数（简称FMI）
- Rand指数（简称RI）
内部指标
- DB指数（简称DBI）
- Dunn指数（简称DI）

距离计算：

$L_p$ 范数
欧氏距离
曼哈顿距离

分类：

原型聚类：k-means算法，学习向量量化（有监督学习），高斯混合聚类都是此类型算法

假设聚类结构能够通过一组原型刻画，然后对原型进行迭代更新求解。

密度聚类：DBSCAN
层次聚类：AGNES

试图在不同层次上对数据集进行划分，分为自底向上的聚合策略和自顶向下的分拆策略

聚簇之间的距离的计算：最小距离，最大距离和平均距离（两个簇中样本点对距离之和取平均）

AGNES算法被相应称为：单链接算法（以最小距离为准），全链接算法（以最大距离为准）和均链接算法

以单链接算法为例：

初始时每个样本点看做一个簇，找到所有簇对中最小的距离，将他们合并为一个簇，此时合并的簇与其他簇的距离更新为两个点到其他簇距离的最小值。
上面的步骤为循环里面的步骤，接着进行下一次循环，找到所有簇中最短的距离，然后将他们合并，合并后更新簇之间的距离为【合并簇中的所有点到其他簇距离的最小值】，一直进行上述循环操作，直到达到指定簇的数量再停止循环。

K-MEANS算法

1 概述

聚类概念：这是个无监督问题（没有标签数据），目的是将相似的东西分到一组。

通常使用的算法是K-MEANS算法

K-MEANS算法：

需要指定簇的个数，即K值
质心：数据的均值，即向量各维取平均即可
距离的度量：常用欧几里得距离和余弦相似度（先标准化，让数据基本都是在一个比较小的范围内浮动）
优化目标： $min\sum \limits_{i = 1}^K \sum \limits_{x \in C_i} dist(c_i, x)^2$ （对于每一个簇让每一个样本到中心点的距离越小越好， $c_i$ 代表中心点）

2 K-MEANS流程

假设平面上有一系列样本点，现在需要将其进行分组。

选定K=2，即将这些数据点分成两个组别。

随机选择两个质心（分别代表两个簇），计算所有样本点到两个质心的距离。每个样本点会计算出到两个质心的距离，那么选择最小的距离，这个样本点就归属于哪个簇。
然后对于两个簇的所有样本点分别算出对应的质心（这两个质心便充当新的质心），再对所有样本点计算到两个新的质心的距离，还是选择最小的距离，那么这个样本点就归属于哪个簇。
最终直到两个簇所属的样本点不在发生变化。

K-MEANS工作流程视频参考

3 优缺点

优点：

简单快速，适合常规数据集

缺点：

K值难以确定
复杂度与样本呈线性关系
很难发现任意形状的簇
初始的点影响很大

K-MEANS可视化演示

4 K-MEANS进行图像压缩

from skimage import io
from sklearn.cluster import KMeans
import numpy as npimage = io.imread("1.jpg")
io.imshow(image)
# io.show()  # 显示图片rows = image.shape[0]
cols = image.shape[1]
print(image.shape)image = image.reshape(rows * cols, 3)
kmeans = KMeans(n_clusters=128, n_init=10, max_iter=100)  # 簇128, 最大迭代次数100
kmeans.fit(image)clusters = np.asarray(kmeans.cluster_centers_, dtype=np.uint8)
labels = np.asarray(kmeans.labels_, dtype=np.uint8)
labels = labels.reshape(rows, cols)print(clusters.shape)
np.save('test.npy', clusters)
io.imsave('compressed.jpg', labels)

DBSCAN算法

1 概述

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，DBSCAN算法将簇定义为密度相连的点的最大集合。

核心对象：若某个点的密度达到算法设定的阈值则称其为核心点。（即r邻域内的点的数量不小于minPts）

基于以上密度的定义，我们可以将样本集中的点划分为以下三类：

核心点：在半径r区域内，含有超过MinPts数目（最小数目）的点，称为核心点；
边界点：在半径r区域内，点的数量小于MinPts数目，但是是核心点的直接邻居；
噪声点：既不是核心点也不是边界点的点

噪声点是不会被聚类纳入的点，边界点与核心点组成聚类的“簇”。

一些概念：

直接密度可达（密度直达）：如果p在q的r领域内，且q是一个核心点对象，则称对象p从对象q出发时直接密度可达，反之不一定成立，即密度直达不满足对称性。
密度可达：如果存在一个对象链q–>e–>a–>k–>l–>p，任意相邻两个对象间都是密度直达的，则称对象p由对象q出发密度可达。密度可达满足传递性。
密度相连：对于 $x_i$ 和 $x_j$ ,如果存在核心对象样本 $x_k$ ，使 $x_i$ 和 $x_j$ 均由 $x_k$ 密度可达，则称 $x_i$ 和 $x_j$ 密度相连。密度相连关系满足对称性。

核心点能够连通（密度可达），它们构成的以r为半径的圆形邻域相互连接或重叠，这些连通的核心点及其所处的邻域内的全部点构成一个簇。

2 原理

DBSCAN通过检查数据集中每个点的r邻域来搜索簇，如果点p的r邻域包含多于MinPts个点，则创建一个以p为核心对象的簇；
然后， DBSCAN迭代的聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并；
当没有新的带你添加到任何簇时，迭代过程结束。

优缺点：

优点：基于密度定义，可以对抗噪声，能处理任意形状和大小的簇
缺点：当簇的密度变化太大时候，聚类得到的结果会不理想；对于高维问题，密度定义也是一个比较麻烦的问题。

3 实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import matplotlib.colors# 创建Figure
fig = plt.figure()
# 用来正常显示中文标签
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
# 用来正常显示负号
matplotlib.rcParams['axes.unicode_minus'] = FalseX1, y1 = datasets.make_circles(n_samples=5000, factor=.6,noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2,centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)# 原始点的分布
ax1 = fig.add_subplot(311)
X = np.concatenate((X1, X2))
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.title(u'原始数据分布')
plt.sca(ax1)# K-means聚类
from sklearn.cluster import KMeans
ax2 = fig.add_subplot(312)
y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title(u'K-means聚类')
plt.sca(ax2)# DBSCAN聚类
from sklearn.cluster import DBSCAN
ax3 = fig.add_subplot(313)
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title(u'DBSCAN聚类')
plt.sca(ax3)plt.show()