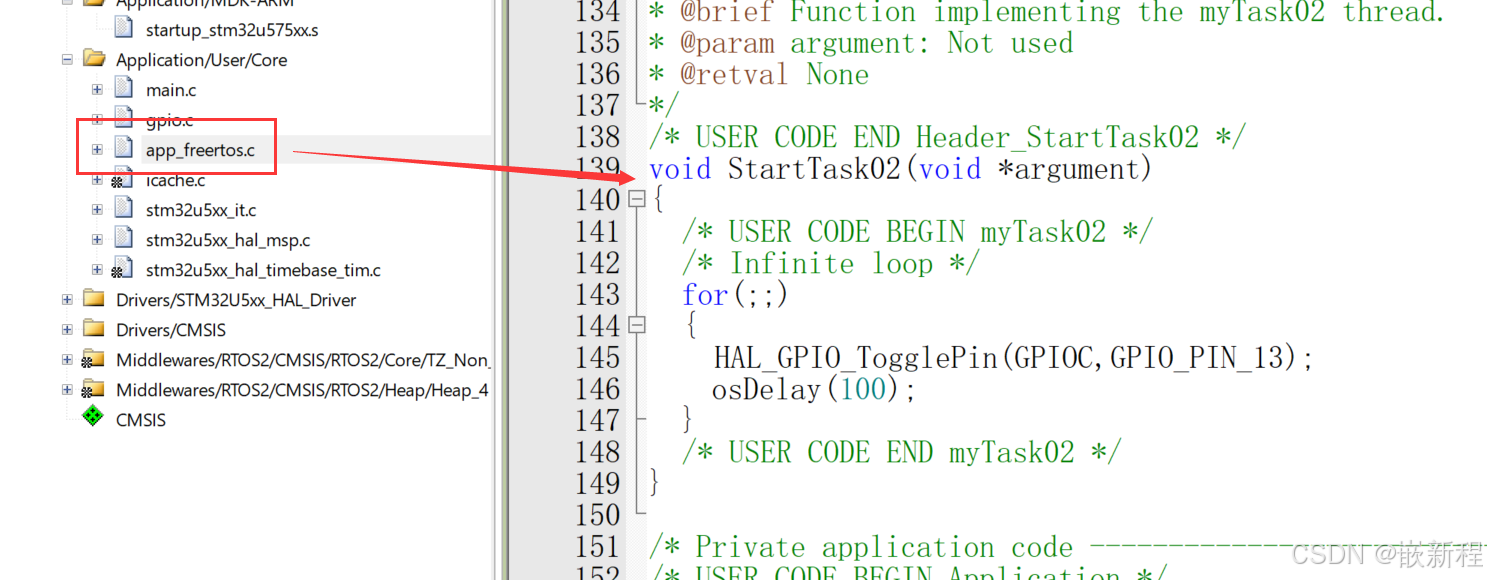
2024/11/10-2024/11/18:
主要对transformer一些比较难理解的点做了一些整理,希望对读者有所帮助。
前置知识:
深度学习基础练习:从pytorch API出发复现LSTM与LSTMP-CSDN博客
【神经网络】学习笔记十四——Seq2Seq模型-CSDN博客
【官方双语】一个视频理解神经网络注意力机制,详细阐释!_哔哩哔哩_bilibili
【官方双语】Transformer模型最通俗易懂的讲解,零基础也能听懂!_哔哩哔哩_bilibili
代码参考:
19、Transformer模型Encoder原理精讲及其PyTorch逐行实现_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1cP4y1V7GF?spm_id_from=333.788.videopod.sections&vd_source=db0d5acc929b82408b1040d67f2b1dde

Chapter 1: Parameter Set
import torch
import torch.nn as nn
import torch.nn.functional as F# 关于word embedding 以序列建模为例
# 考虑source sentence 和 target sentence
# 构建序列,序列的字符以其在词表中的索引形式表示
torch.manual_seed(42)batch_size = 2
# 单词表大小(即设只有8种单词)
max_num_src_words = 8
max_num_tgt_words = 8
model_dim = 8# 序列的最长长度
max_src_seq_len = 5
max_tgt_seq_len = 5
# 序列编码的最大长度
max_position_len = 5src_len = torch.randint(2, 5, (batch_size,))
tgt_len = torch.randint(2, 5, (batch_size,))
"""
例:
tensor([2, 4]) src_seq 第一个句子长度为2 第二个句子长度为4
tensor([3, 3]) tgt_seq 第一个句子长度为3 第二个句子长度为3
"""
# 以单词索引构成的句子
# 加入pad使每个句子的长度相同:因为每批的句子都要做统一处理,做相同的矩阵运算,所以同一批次的句子不能是长短不一的向量
src_seq = torch.stack([F.pad(torch.randint(1, max_num_src_words, (L,)), (0, max_src_seq_len-L)) for L in src_len])
tgt_seq = torch.stack([F.pad(torch.randint(1, max_num_tgt_words, (L,)), (0, max_tgt_seq_len-L)) for L in tgt_len])最后两句代码的可读性不是很好,这里print解释一下:
origin: [tensor([5, 4]), tensor([6, 6, 1, 1])] [tensor([1, 6, 7]), tensor([5, 2, 3])] ===> after pad: [tensor([5, 4, 0, 0, 0]), tensor([6, 6, 1, 1, 0])] [tensor([1, 6, 7, 0, 0]), tensor([5, 2, 3, 0, 0])] ===> after stack: tensor([[5, 4, 0, 0, 0], 第一个输入[6, 6, 1, 1, 0]]) 第二个输入 tensor([[1, 6, 7, 0, 0], 第一个需要预测的输出[5, 2, 3, 0, 0]]) 第二个需要预测的输出
在这个阶段,我们生成了输入以及需要预测的输出并用pad将其对齐,这里使用pad将空位填充为0。
Chapter 2: Word Embedding

# 构造embedding,将每一种字母索引映射为model_dim位的embedding
# 词表有[1-8)共7个字母索引,pad用0填充空位,所以共有8种索引,每种索引用8个浮点数构成的列表表示
src_embedding_table = nn.Embedding(max_num_src_words, model_dim)
tgt_embedding_table = nn.Embedding(max_num_tgt_words, model_dim)
# print(src_embedding_table.weight)embedding可以理解为将每个字母的索引(下文也可能将字母索引说成单词索引,这两个意思一样)用一个model_dim位数的浮点数序列来表征。
这里放一下src_embedding_table的内容 :
src_embedding_table torch.Size([8, 8]) Parameter containing: tensor([[ 1.6423, -0.1596, -0.4974, 0.4396, -0.7581, 1.0783, 0.8008, 1.6806],[ 1.2791, 1.2964, 0.6105, 1.3347, -0.2316, 0.0418, -0.2516, 0.8599],[-1.3847, -0.8712, -0.2234, 1.7174, 0.3189, -0.4245, 0.3057, -0.7746],[-1.5576, 0.9956, -0.8798, -0.6011, -1.2742, 2.1228, -1.2347, -0.4879],[-0.9138, -0.6581, 0.0780, 0.5258, -0.4880, 1.1914, -0.8140, -0.7360],[-1.4032, 0.0360, -0.0635, 0.6756, -0.0978, 1.8446, -1.1845, 1.3835],[ 1.4451, 0.8564, 2.2181, 0.5232, 0.3466, -0.1973, -1.0546, 1.2780],[-0.1722, 0.5238, 0.0566, 0.4263, 0.5750, -0.6417, -2.2064, -0.7508]],requires_grad=True)
生成embedding table之后,就可以将原始数据根据每个字母的索引将其转化为对应的浮点数编码:
src_embedding = src_embedding_table(src_seq)
tgt_embedding = tgt_embedding_table(tgt_seq)
# print(src_embedding)生成结果如下:
共两句,每句五个单词索引(包括填充的0),每个单词索引由8个浮点数表示 src_embedding.shape: torch.Size([2, 5, 8]) src_embedding: tensor([[[-1.4032, 0.0360, -0.0635, 0.6756, -0.0978, 1.8446, -1.1845,1.3835],[-0.9138, -0.6581, 0.0780, 0.5258, -0.4880, 1.1914, -0.8140,-0.7360],[ 1.6423, -0.1596, -0.4974, 0.4396, -0.7581, 1.0783, 0.8008,1.6806],[ 1.6423, -0.1596, -0.4974, 0.4396, -0.7581, 1.0783, 0.8008,1.6806],[ 1.6423, -0.1596, -0.4974, 0.4396, -0.7581, 1.0783, 0.8008,1.6806]],[[ 1.4451, 0.8564, 2.2181, 0.5232, 0.3466, -0.1973, -1.0546,1.2780],[ 1.4451, 0.8564, 2.2181, 0.5232, 0.3466, -0.1973, -1.0546,1.2780],[ 1.2791, 1.2964, 0.6105, 1.3347, -0.2316, 0.0418, -0.2516,0.8599],[ 1.2791, 1.2964, 0.6105, 1.3347, -0.2316, 0.0418, -0.2516,0.8599],[ 1.6423, -0.1596, -0.4974, 0.4396, -0.7581, 1.0783, 0.8008,1.6806]]], grad_fn=<EmbeddingBackward0>)
可以看到 src_embedding相比于src_seq多出了一个维度且大小为8,跟前面的解释相符合。
Chapter 3: Position Embedding

该步骤在word embedding之后,是为了强调输入的位置信息,这一步是比较重要的,比如Bob killed John 和 John killed Bob 虽然单词都相同,但是表达的意思完全相反。位置编码就是为了让模型捕获到这一部分的信息。
下面是论文中位置编码相关的公式,pos指单词在句子中的位置(从头开始数),i指用来表征每个单词索引的word embedding中每个元素的对应位置:

# 构建position embedding 位置编码 针对每个句子,即每个句子的[5(单词数量), 8(embedding编码)]
# 公式中的列标 [0, 5)
pos_mat = torch.arange(max_position_len).reshape((-1, 1))
print(pos_mat)
# 公式中的行标 [0, 2, 4, 6]
i_mat = torch.pow(10000, torch.arange(0, 8, 2).reshape((1, -1)) / model_dim)
print(i_mat)# 生成每个单词索引位置对应的位置编码
pe_embedding_table = torch.zeros(max_position_len, model_dim)
# 偶数列
pe_embedding_table[:, 0::2] = torch.sin(pos_mat / i_mat)
# 奇数列
pe_embedding_table[:, 1::2] = torch.cos(pos_mat / i_mat)# print(pe_embedding_table)
# 构建新的embedding并将其权重用之前计算的位置编码覆写
pe_embedding = nn.Embedding(max_position_len, model_dim)
pe_embedding.weight = nn.Parameter(pe_embedding_table, requires_grad=False)src_pos = torch.cat([torch.unsqueeze(torch.arange(max_src_seq_len), 0) for _ in range(batch_size)]).to(torch.int32)
tgt_pos = torch.cat([torch.unsqueeze(torch.arange(max_tgt_seq_len), 0) for _ in range(batch_size)]).to(torch.int32)这里放一下src_pos和tgt_pos的print:
tensor([[0, 1, 2, 3, 4],[0, 1, 2, 3, 4]], dtype=torch.int32) tensor([[0, 1, 2, 3, 4],[0, 1, 2, 3, 4]], dtype=torch.int32)
请注意这还不是位置编码,只是每个元素的行列信息和位置编码的一些前置参数,接下来我们根据论文里的公式来:
src_pe_embedding = pe_embedding(src_pos)
tgt_pe_embedding = pe_embedding(tgt_pos)
# print(src_pe_embedding)因为position embedding需要直接与word embedding相加,所以我们也把它做成一个同样shape的张量,这样就可以为每个词添加上位置信息,值得注意的是,位置编码只与单词在所属句子中的位置有关,跟句子之间的相对位置无关,即如果有两个单词各自是一个句子中的第一个单词,他们的位置编码相同:
src_pe_embedding.shape: torch.Size([2, 5, 8]) src_pe_embedding: tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,1.0000e+00, 0.0000e+00, 1.0000e+00],[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,9.9995e-01, 1.0000e-03, 1.0000e+00],[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,9.9980e-01, 2.0000e-03, 1.0000e+00],[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,9.9955e-01, 3.0000e-03, 1.0000e+00],[-7.5680e-01, -6.5364e-01, 3.8942e-01, 9.2106e-01, 3.9989e-02,9.9920e-01, 4.0000e-03, 9.9999e-01]],[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,1.0000e+00, 0.0000e+00, 1.0000e+00],[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,9.9995e-01, 1.0000e-03, 1.0000e+00],[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,9.9980e-01, 2.0000e-03, 1.0000e+00],[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,9.9955e-01, 3.0000e-03, 1.0000e+00],[-7.5680e-01, -6.5364e-01, 3.8942e-01, 9.2106e-01, 3.9989e-02,9.9920e-01, 4.0000e-03, 9.9999e-01]]])
这公式为什么要这么做?简单来说这可以给句子中的每个单词生成一个独一无二的位置编码,避免位置编码重复。除此之外,将正余弦函数作为position embedding还可以提高模型的泛化能力,即使在推理阶段遇到了比训练中最大序列还要长的句子,也可以通过训练中某个位置位置编码的线性组合得到更长位置的位置编码。
Chapter 4: Encoder Self-attention Mask


4.1 MatMul
注意力机制其实就是对一个句子序列算出一个新的表征。注意力权重是通过Query和Key的相似度来计算的,而这两者又都是基于上面的word embedding经过几个线性层计算出来的。

上面这张图代表了这个阶段的操作。对于整个句子而言,Query和Key是两个矩阵,而如果对应到每个具体单词上面,这两者又是两个向量。因此,两个矩阵做内积便能得到每个单词与其他单词的相似度。
4.2 Scale

除此之外,理解公式中的Scale——分母dk(隐含层大小)也有些困难。我们都知道在训练时神经网络会进行反向传播来修正参数,而修正参数的幅度有与计算出的雅可比行列式中各个元素的值有关,这里直接借用视频中的一张图来说明:

reference Transformer模型Encoder原理精讲及其PyTorch逐行实现 1:22:56
在这张图上我们可以看到给一系列随机数 *10 和 /10 之后再经过softmax,他们计算得到的雅可比行列式的值是不一样的。在 *10 之后,计算出的梯度比较“尖锐”,也就是方差较大,有的梯度较大,有的梯度却极小,这并不利于模型的收敛。而在 /10 之后,计算出的梯度便平缓了许多,这意味着每个参数都可以在反向传播中得到有效的修正。并且,我们在数学角度上可以证明将根号dk作为分母能将矩阵点乘的方差缩小为1。
如上图,计算完单词之间的相似度之后,再经过softmax归一化就能得到0-1之间的归一化值。因为softmax的单调特性,相似度越大则经过softmax之后的值越大。
4.3 Mask

接下来,我们开始对还记得我们在word embedding阶段创建的输入吗?
tensor([[5, 4, 0, 0, 0], 第一个输入 原长度为2,填充两个0
[6, 6, 1, 1, 0]]) 第二个输入 原长度为4,填充一个0
当时使用了0来对句子进行填充,将句子向量强行扩充为5维。而在计算self-attention的阶段,我们只对句子的有效长度进行attention计算。这就需要遮住无效的部分(所谓无效的部分下文有解释)。如果在这些位置上补一些无穷小(负无穷)的值,经过softmax操作,这些值在输出之后就会变为0,从而避免对全局概率产生影响。
因此,有如下代码:
# 构建encoder的self-attention mask
# mask.shape: [batch_size, max_src_seq_len, max_src_seq_len], 值为1或-inf
valid_encoder_pos_matrix = torch.stack([F.pad(torch.ones(L, L), (0, max_src_seq_len-L, 0, max_src_seq_len-L)) for L in src_len])
masked_encoder_self_attention = valid_encoder_pos_matrix == 0masked_encoder_self_attention: tensor([[[False, False, True, True, True],[False, False, True, True, True],[ True, True, True, True, True],[ True, True, True, True, True],[ True, True, True, True, True]],[[False, False, False, False, True],[False, False, False, False, True],[False, False, False, False, True],[False, False, False, False, True],[ True, True, True, True, True]]])
如果你并没有很理解该章节所展示的mask原理,那么可能你会对掩码的矩阵矩阵形式产生一点疑问,这里稍微做一下补充:
Q:为什么输入的是1*5个词的句子,所采用的mask却是5*5?
A:mask遮掩的是词向量之间的关系。如上面所说,在Scale Dot-Product Attention阶段,对于整个句子而言,Query和Key是两个矩阵,而如果对应到每个具体单词上面,这两者又是两个向量,即Q和K中的第一行表征第一个单词,第二行表征第二个单词。
而这两个矩阵又是通过word embedding经过线性层计算出来的,因此,两者的shape应该为(句子中的单词数量n * hidden),因此,Q可以与K的转置矩阵做点积。
而这个输出的相似度矩阵中,位置(1, 1)的元素是第一个词与自身的相似度,位置(1, 2)的元素是第一个词与第二个词的相似度.....以此类推。若我们的句子中只有两个单词,类似于(1, 3)或者(3, 3)这种位置就是不应该存在的——因为句子中并不存在第三个单词。
为了方便统一处理,这个位置我们之前填充的是0。但是神经网络并不知道这个地方是“空”的,那就只能使用mask来提示后面的softmax不要让这些地方的值影响全局概率的预测。因此,mask的维度是(词个数*词个数),对非法的位置设置为true,在后面的代码中进行填充-inf来遮掩。
score = torch.randn(batch_size, max_src_seq_len, max_src_seq_len)
masked_score = score.masked_fill(masked_encoder_self_attention, float("-inf"))
prob = masked_score.softmax(dim=-1)
print(prob)在masked_score中,我们就根据mask矩阵对一个随机生成的矩阵进行了掩码操作,看看效果:
prob: tensor([[[0.5660, 0.4340, 0.0000, 0.0000, 0.0000],[0.6870, 0.3130, 0.0000, 0.0000, 0.0000],[ nan, nan, nan, nan, nan],[ nan, nan, nan, nan, nan],[ nan, nan, nan, nan, nan]],[[0.1508, 0.1173, 0.1579, 0.5740, 0.0000],[0.4315, 0.1342, 0.1746, 0.2597, 0.0000],[0.1446, 0.2971, 0.2774, 0.2809, 0.0000],[0.1549, 0.5402, 0.1237, 0.1812, 0.0000],[ nan, nan, nan, nan, nan]]])
第一个矩阵对应第一个只有两个单词的句子。根据我们上文做出的Answer,矩阵的(1, 1)、(1, 2)、(2, 1)、(2, 2)都是对应的两个词之间的相似度关系,而此外的位置显然是“非法”的。以第一行为例 ,该行代表第一个词与其他所有词的相似度关系,在对非法位置置为-inf再计算softmax之后,第一个词只有与自身和第二个词有相似度关系,和其他不存在的位置则没有。
这就是mask的生效机制。
Chapter 5: Intra-attention Mask
在这个模块中,输出部分在经过第一个注意力模块后输出的值作为Query,Input模块中的输出作为Key和Value,再进行一次注意力的计算。

该模块的重点是不同词数量的句子之间的相似度计算,其实与上个章节的内容基本相同,这里直接贴代码:
# 构建intra-attention mask
# Q @ K.T shape: [batch_size, tgt_seq_len, src_seq_len]
valid_encoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max_src_seq_len-L)), 0) for L in src_len], 0), 2)
# print(valid_encoder_pos)
valid_decoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max_tgt_seq_len-L)), 0) for L in tgt_len], 0), 2)
# print(valid_decoder_pos)
valid_cross_pos = torch.bmm(valid_decoder_pos, valid_encoder_pos.transpose(1, 2))
invalid_cross_pos_matrix = valid_cross_pos == 0然后print一下:
tensor([[[False, False, True, True, True],[False, False, True, True, True],[False, False, True, True, True],[ True, True, True, True, True],[ True, True, True, True, True]],[[False, False, False, False, True],[False, False, False, False, True],[False, False, False, False, True],[ True, True, True, True, True],[ True, True, True, True, True]]])
简单解释一下 ,还记得我们的原始数据吗?
tensor([[5, 4, 0, 0, 0], 第一个输入
[6, 6, 1, 1, 0]]) 第二个输入
tensor([[1, 6, 7, 0, 0], 第一个需要预测的输出
[5, 2, 3, 0, 0]]) 第二个需要预测的输出
类比于上个章节的内容,我们需要注意的是:句子中的词不再和本句子中的词计算相似度了,而是和需要预测的输出中的词来计算相似度,Query矩阵现在表征的是需要输出的句子。
以得到的第一个bool矩阵为例,(1, 1)位置的数据是第一个输出中的第一个词与输入的第一个词的关系,(1, 3)位置的词是第一个输出中的第1个词与输入的第3个词的关系——因为输入并没有第三个词,所以我们在此设置为True来做掩码......以此类推。
Chapter 6: Decoder Self-attention Mask
这里稍微往前推一下,写一下decoder的self-attention mask。

这个mask也有人说是维持因果性的mask。它的思路很简单,如果用于流式的预测和生成,那么在预测下一个词的时候,很显然训练模型不能用下一个词的信息来训练,只能用之前的数据,这就需要一个下三角矩阵shape的mask来做到。
tril_matrix = [F.pad(torch.tril(torch.ones(L, L)), (0, max_tgt_seq_len-L, 0, max_tgt_seq_len-L)) for L in tgt_len]
valid_decoder_tri_matrix = torch.stack(tril_matrix)
# print(valid_decoder_tri_matrix)
invalid_decoder_tri_matrix = valid_decoder_tri_matrix == 0tensor([[[False, True, True, True, True],[False, False, True, True, True],[False, False, False, True, True],[ True, True, True, True, True],[ True, True, True, True, True]],[[False, True, True, True, True],[False, False, True, True, True],[False, False, False, True, True],[ True, True, True, True, True],[ True, True, True, True, True]]])
这个mask是对于输出而言的,而我们的两个需要预测的输出都有三个词,因此是两个3*3的矩阵。现在以第一个矩阵为例讲一下:第一行意思是已经预测完第一个词,开始预测第二个,那肯定要把后面的全遮住,后面几行同理。
score = torch.randn(batch_size, max_tgt_seq_len, max_tgt_seq_len)
masked_score = score.masked_fill(invalid_decoder_tri_matrix, float("-inf"))tensor([[[ 1.0441, -inf, -inf, -inf, -inf],
[ 0.0854, -1.3793, -inf, -inf, -inf],
[ 0.5239, -0.2694, -1.6191, -inf, -inf],
[ -inf, -inf, -inf, -inf, -inf],
[ -inf, -inf, -inf, -inf, -inf]],[[ 0.7337, -inf, -inf, -inf, -inf],
[ 2.0207, 0.2539, -inf, -inf, -inf],
[ 2.5574, 0.5716, 1.3596, -inf, -inf],
[ -inf, -inf, -inf, -inf, -inf],
[ -inf, -inf, -inf, -inf, -inf]]])
模拟一下mask之后计算相似度的效果:
prob = masked_score.softmax(dim=-1)tensor([[[1.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.8123, 0.1877, 0.0000, 0.0000, 0.0000],
[0.6371, 0.2882, 0.0747, 0.0000, 0.0000],
[ nan, nan, nan, nan, nan],
[ nan, nan, nan, nan, nan]],[[1.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.8541, 0.1459, 0.0000, 0.0000, 0.0000],
[0.6949, 0.0954, 0.2097, 0.0000, 0.0000],
[ nan, nan, nan, nan, nan],
[ nan, nan, nan, nan, nan]]])
Chapter 6: Scaled Self-attention
这部分很简单,其实就是写下这个公式的函数。

代码如下,就不再赘述了:
# 构建scaled self-attention
def scaled_dot_product_attention(Q, K, V, mask):# shape of Q K V: [batch_size, seq_len, model_dim]d_k = Q.shape[-1]scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k).float())if mask is not None:scores = scores.masked_fill(mask, float("-inf"))prob = F.softmax(scores, dim=-1)return torch.matmul(prob, V)