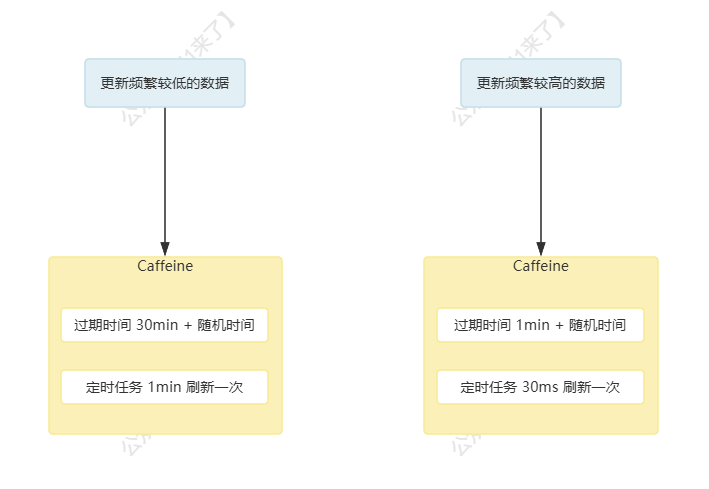
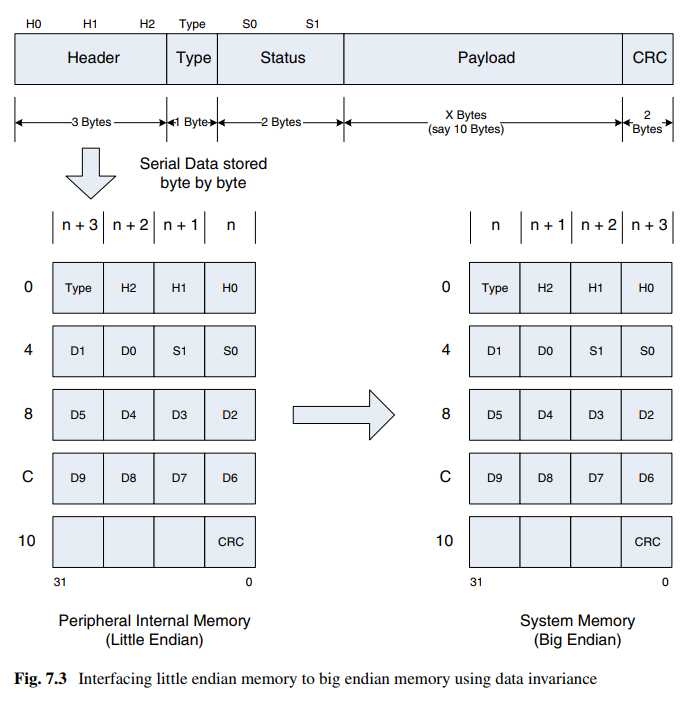
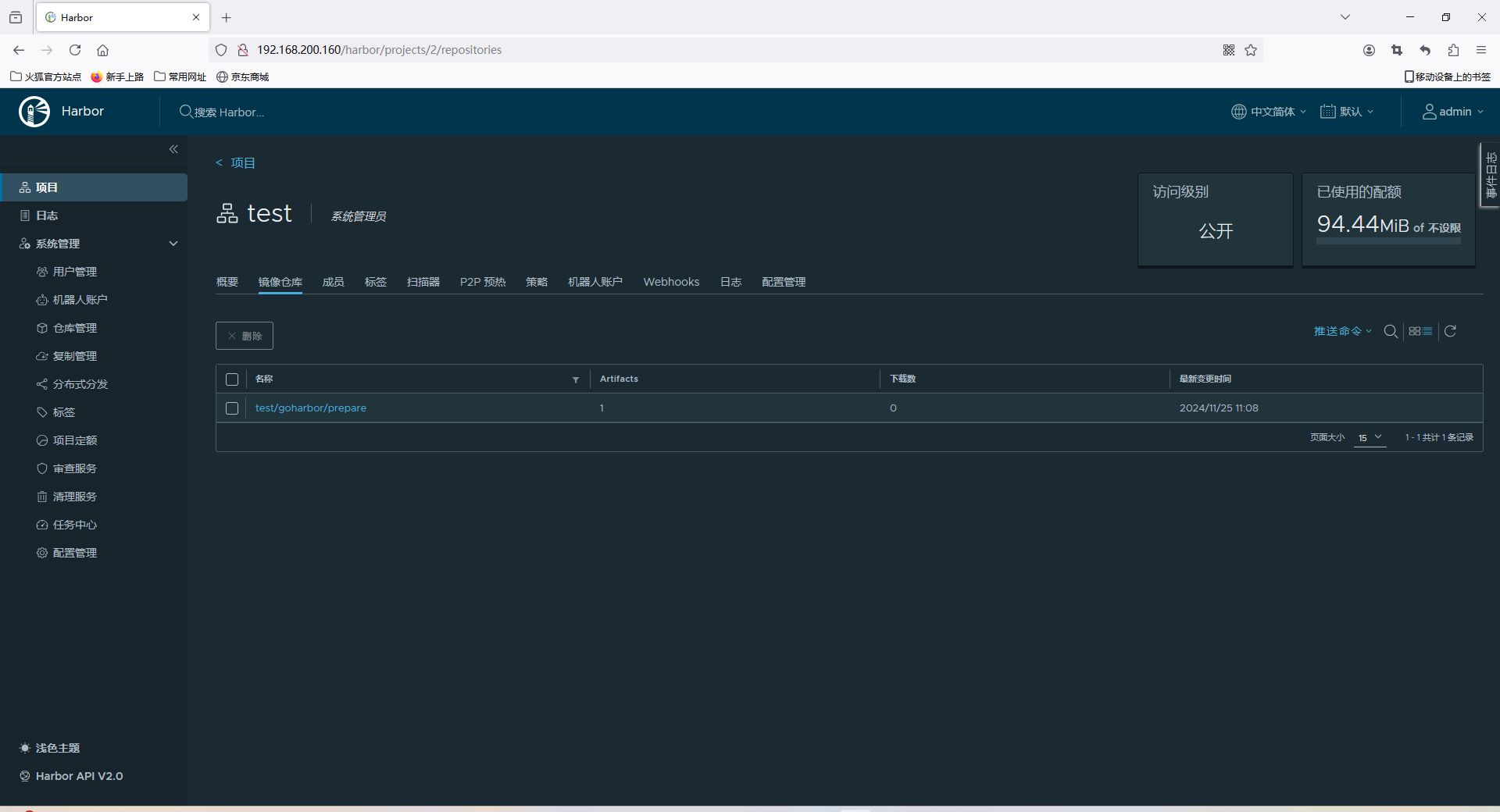
转换矩阵引用了库nalgebra,使用时研究具体实现。
use std::ops;use nalgebra::Perspective3;use crate::Scalar;use super::{Aabb, LineSegment, Point, Triangle, Vector};/// An affine transform
#[repr(C)]
#[derive(Debug, Clone, Copy, Default)]
pub struct Transform(nalgebra::Transform<f64, nalgebra::TAffine, 3>);impl Transform {/// Construct an identity transformpub fn identity() -> Self {Self(nalgebra::Transform::identity())}/// Construct a translationpub fn translation(offset: impl Into<Vector<3>>) -> Self {let offset = offset.into();Self(nalgebra::Transform::from_matrix_unchecked(nalgebra::OMatrix::new_translation(&offset.to_na()),))}/// Construct a rotation////// The direction of the vector defines the rotation axis. Its length/// defines the angle of the rotation.pub fn rotation(axis_angle: impl Into<Vector<3>>) -> Self {let axis_angle = axis_angle.into();Self(nalgebra::Transform::from_matrix_unchecked(nalgebra::OMatrix::<_, nalgebra::Const<4>, _>::new_rotation(axis_angle.to_na(),),))}/// Construct a scalingpub fn scale(scaling_factor: f64) -> Self {Self(nalgebra::Transform::from_matrix_unchecked(nalgebra::OMatrix::new_scaling(scaling_factor),))}/// # Extract the "right" vector from the rotational componentpub fn right(&self) -> Vector<3> {let d = self.data();Vector::from([d[0], d[1], d[2]])}/// # Extract the "up" vector from the rotational componentpub fn up(&self) -> Vector<3> {let d = self.data();Vector::from([d[4], d[5], d[6]])}/// Transform the given pointpub fn transform_point(&self, point: &Point<3>) -> Point<3> {Point::from(self.0.transform_point(&point.to_na()))}/// Inverse transform given pointpub fn inverse_transform_point(&self, point: &Point<3>) -> Point<3> {Point::from(self.0.inverse_transform_point(&point.to_na()))}/// Transform the given vectorpub fn transform_vector(&self, vector: &Vector<3>) -> Vector<3> {Vector::from(self.0.transform_vector(&vector.to_na()))}/// Transform the given segmentpub fn transform_segment(&self,segment: &LineSegment<3>,) -> LineSegment<3> {let [a, b] = &segment.points;LineSegment::from([self.transform_point(a), self.transform_point(b)])}/// Transform the given trianglepub fn transform_triangle(&self, triangle: &Triangle<3>) -> Triangle<3> {let [a, b, c] = &triangle.points;Triangle::from([self.transform_point(a),self.transform_point(b),self.transform_point(c),])}/// Inverse transformpub fn inverse(&self) -> Self {Self(self.0.inverse())}/// Transpose transformpub fn transpose(&self) -> Self {Self(nalgebra::Transform::from_matrix_unchecked(self.0.to_homogeneous().transpose(),))}/// Project transform according to camera specification, return data as an array./// Used primarily for graphics code.pub fn project_to_array(&self,aspect_ratio: f64,fovy: f64,znear: f64,zfar: f64,) -> [Scalar; 16] {let projection = Perspective3::new(aspect_ratio, fovy, znear, zfar);let mut array = [0.; 16];array.copy_from_slice((projection.to_projective() * self.0).matrix().as_slice(),);array.map(Scalar::from)}/// Return a copy of the inner nalgebra transformpub fn get_inner(&self) -> nalgebra::Transform<f64, nalgebra::TAffine, 3> {self.0}/// Transform the given axis-aligned bounding boxpub fn transform_aabb(&self, aabb: &Aabb<3>) -> Aabb<3> {Aabb {min: self.transform_point(&aabb.min),max: self.transform_point(&aabb.max),}}/// Exposes the data of this Transform as a slice of f64.pub fn data(&self) -> &[f64] {self.0.matrix().data.as_slice()}/// Extract the rotation component of this transformpub fn extract_rotation(&self) -> Self {Self(nalgebra::Transform::from_matrix_unchecked(self.0.matrix().fixed_resize::<3, 3>(0.).to_homogeneous(),))}/// Extract the translation component of this transformpub fn extract_translation(&self) -> Self {*self * self.extract_rotation().inverse()}
}impl ops::Mul<Self> for Transform {type Output = Self;fn mul(self, rhs: Self) -> Self::Output {Self(self.0.mul(rhs.0))}
}#[cfg(test)]
mod tests {use approx::assert_abs_diff_eq;use crate::{Scalar, Vector};use super::Transform;#[test]fn extract_rotation_translation() {let rotation =Transform::rotation(Vector::unit_z() * (Scalar::PI / 2.));let translation = Transform::translation([1., 2., 3.]);assert_abs_diff_eq!((translation * rotation).extract_rotation().data(),rotation.data(),epsilon = 1e-8,);assert_abs_diff_eq!((translation * rotation).extract_translation().data(),translation.data(),epsilon = 1e-8,);assert_abs_diff_eq!((rotation * translation).extract_rotation().data(),rotation.data(),epsilon = 1e-8,);assert_abs_diff_eq!((rotation * translation).extract_translation().data(),Transform::translation([-2., 1., 3.]).data(),epsilon = 1e-8,);}
}