BA和CS算法中的Levy飞行策略

Levy飞行策略通过模拟自然界中动物的长距离迁徙行为，指导粒子进行更大范围的搜索，有助于算法快速找到全局最优解。它是一种具有独特优势的随机行为策略，模拟随机游走或搜索过程中的步长和方向，其步长的概率分布为重尾分布，意味着在随机行走的过程中有相对较高的概率出现大跨步。

一、BA和CS算法中的Levy飞行策略

1. 布谷鸟搜索算法（Cuckoo Search, CS）

布谷鸟搜索算法是一种基于自然现象的启发式优化算法，它模拟了布谷鸟寻找宿主鸟巢并寄生卵的行为。在布谷鸟搜索算法中，Levy飞行被用来模拟布谷鸟在搜索过程中的随机游走模式。通过Levy飞行，布谷鸟能够高效地探索搜索空间，从而找到更好的鸟巢位置。这种策略使得算法能够跳出局部最优解，提高全局搜索能力。可以先了解我的文章：路径规划之启发式算法之十一：布谷鸟搜索算法（Cuckoo Search，CS）-CSDN博客

2. 蝙蝠算法（Bat Algorithm, BA）

蝙蝠算法是一种基于蝙蝠回声定位行为的启发式优化算法。在蝙蝠算法中，Levy飞行也被用来模拟蝙蝠在搜索过程中的随机移动。蝙蝠通过调整其飞行速度和方向来探索搜索空间，并利用回声定位来感知环境中的障碍物和目标。Levy飞行的引入使得蝙蝠算法能够更好地平衡局部搜索和全局搜索，从而提高算法的搜索效率和精度。可以先了解我的文章：路径规划之启发式算法之十：蝙蝠算法（Bat Algorithm, BA）-CSDN博客

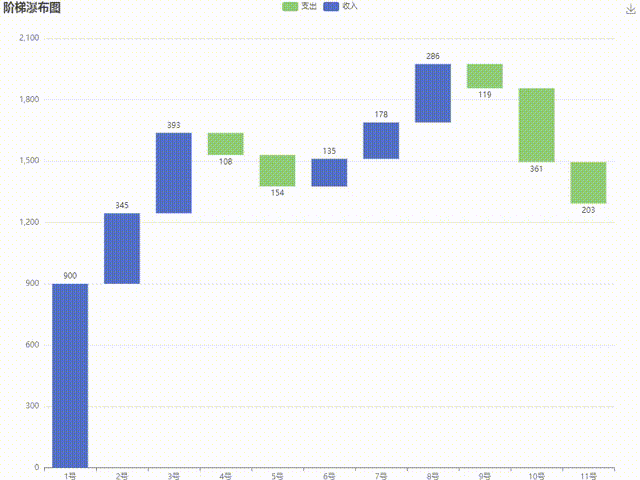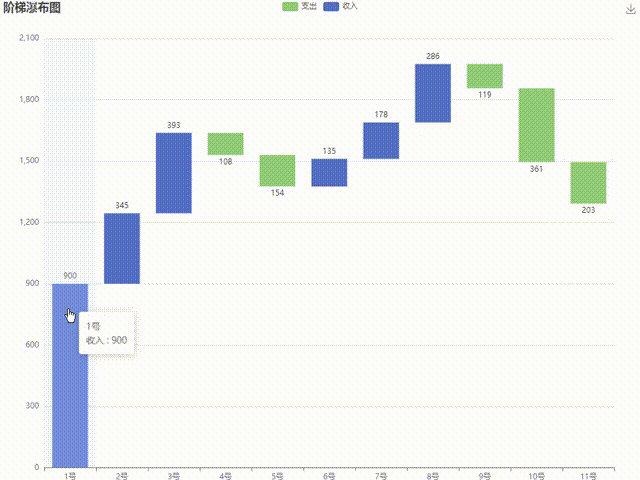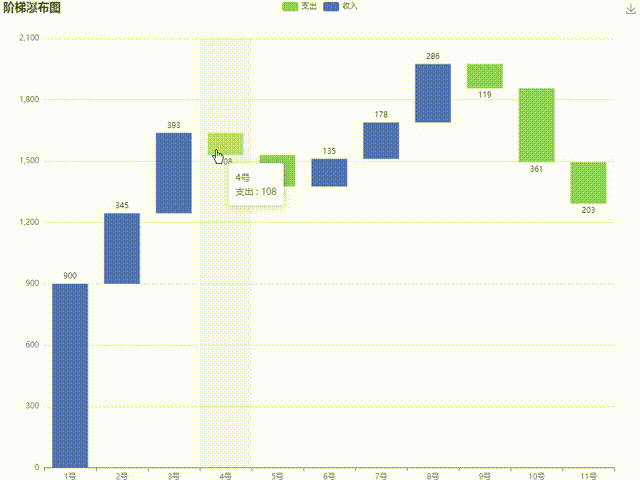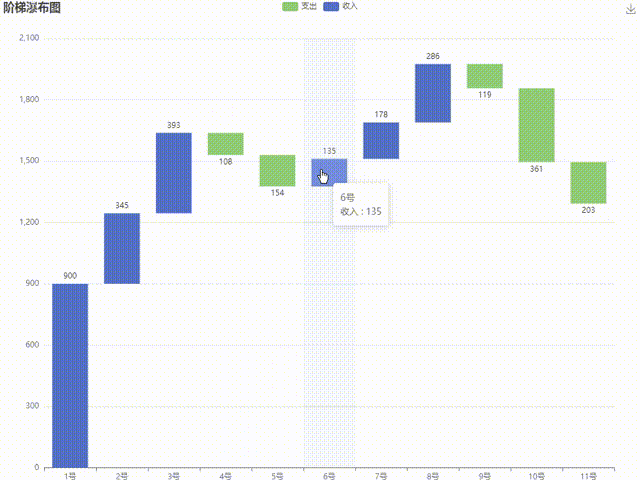
Levy飞行策略在算法中的应用

图1 Levy飞行策略在算法中的应用

二、定义

1. Levy飞行策略

Levy飞行策略的名称来自于莱维飞行（Levy flight），它模拟了在某些情况下生物在搜索食物或资源时的运动方式。这种策略使得个体或粒子在空间中进行随机移动，其步长和方向由莱维分布所决定。

2. Levy分布（Lévy过程）

莱维分布最早由法国数学家Paul Lévy于20世纪20年代提出，是一种具有重尾特性的概率分布，长尾行为使得在尾部产生极端值的概率较高。其概率密度函数满足幂律关系，意味着相对较大的步长事件（即远距离的移动）比正态分布或其他常见分布更加频繁地发生。与传统分布相比，莱维分布无法定义方差，且不存在矩，这使得它在统计特性上与正态分布等传统分布有着本质的区别。

Lévy分布的定义：一个随机过程 $X_{t}$ ，如果满足三个条件，即 $X_{0}=0$ 、增量平稳独立、以及连续时刻处于概率1的状态时处处右连续，那么它就是一个Lévy过程。数学表达如下：

三个条件详解：

（1）第一个条件要求起始点为0，这使得我们可以将其看作是从原点出发的轨迹。

（2）第二个条件则表明Lévy过程的增量具有平稳性和独立性，也就是说，无论我们选择观察的时间段长短如何，增量的统计性质都是相同的，并且不同时间段的增量之间是独立的。这一特性使得Lévy过程成为了描述许多自然现象和金融市场中的波动性的重要工具。

（3）第三个条件强调了Lévy过程在连续时刻处于概率1的状态时处处右连续。简单来说，这意味着Lévy过程在任意时刻t的取值都是连续的。这种连续性的要求与我们熟悉的布朗运动（Brownian Motion）有所不同，后者的轨迹是不连续的。正是这种连续性使得Lévy过程能够更好地描述某些现象，如股票价格的变化、微粒的扩散以及蛋白质的折叠等。