光栅化(三角形的离散化)(Rasterization1 (Triangles))
接着上面的透视投影开始:
如何确定一个近平面的 l(left) , r(right) , b(bottom) , t(top)四个面?通常使用竖直可视角度(vertical field-of-view , fovY)和长宽比(aspect ration)来确定
fovY就是链接Camera底面的中点和顶面的中点所成的角度,长宽比 = width/height。

如何确定近平面的长和宽?知道Camera到近平面的距离,然后就可以通过fovY来计算

在MVP之后应该接着做什么?
回顾一下MVP:
- model transformation(placing objects)
- view transformation(placing camera)
- Projection transformation
- Orthographic projection(cuboid to “canonical” cube [-1,1]^3)(长方体转换到规范立方体当中)
- Perspective projection(frustum to “canonical” cube)(平截头体转换为规范立方体)
在最后投影变换结束后,我们所需要的图像被投影到了规范立方体中,那么应该对规范立方体进行怎样的处理?
将规范立方体的投影显示到屏幕上(Screen)
什么是屏幕?
- 屏幕是由一系列的像素所组成的
- 像素的个数,或者说二维像素数组的大小,称为屏幕的解析度。如1920*1080.
- 屏幕是一个典型的光栅显示设备
那什么是像素?
- 我们现在认为,像素是颜色均匀的小方块,并且不会改变(伪)
- 其颜色是rgb的混合
屏幕空间
怎么定义一个屏幕空间?一个屏幕空间是一个二维的像素的数组,如图所示,

有几点要注意:
- 像素的坐标(或者说在数组中的索引)(x,y)总是一个整数
- 像素的坐标是(0,0)到(width - 1, height - 1)这个范围之内的。width和height为屏幕的宽高,如1920*1080
- 像素(x,y)的坐标的中心为(x+0.5 , y+0.5),如上图蓝色的点,坐标为(2,1),中心为(2.5,1.5)
- 屏幕的范围为(0,0)到 (width, height)
将规范立方体转化到屏幕空间上
在转化时有两点要注意:
- 与z无关(z的值其实是物体在世界空间中的深度值,但是目前我们只有一个物体,所以不考虑他)
- 对xOy平面进行转换,[-1,1]^2转换到 [0,width] × [0,height]

对xOy平面转换的矩阵为:

称之为视口矩阵。对这个矩阵进行解析:
首先要先对其进行位移,因为规范立方体中的中心位于原点的位置,而屏幕空间的坐标是从左下角开始为原点(0,0),不存在负坐标,所以先将规范立方体的中心移动到(width/2,height/2)的位置,然后再对规范立方体进行拉伸,拉伸比例如矩阵所示。因为与z无关,所以对z不做任何变换。
什么是光栅化?
光栅化就是将投影的内容画到屏幕上的过程,其过程就如上面所说,最终将规范立方体的内容画到了屏幕上,这个过程就是光栅化。


这个老虎就是计算机图形学所做出来的结果,其是由许多的任意四边形组成的,每个四边形上的像素都是均匀的。
三角形 - 最基本的图元
为什么使用三角形作为最基本的图元(图元:组成图形的基本单位)?
- 三角形是最基础的多边形,若是去掉一条边则就会成为线段,不能再成 多边形
- 任何多边形都能够分解成三角形的组合
- 三角形还有一些优秀的性质:
- 三角形一定是平面的,而不会是折面或者曲面(试想一下把一个正方形的中心点拽起来会发生什么?)
- 三角形能够明确区分内外(判断一个点是在三角形内还是外,之前的课程中有提到过,使用叉乘)
- 三角形上有着明确的插值方法(如定义一个三角形,三个点的颜色分别是红绿蓝,那么这个三角形就会有一个渐变的颜色效果,这就是颜色插值,下图就是插值效果,只定义了三个顶点的颜色,中间的渐变的颜色全都是插值效果)

三角形作为图元的例子:


既然图元为三角形,我们最终还是要用像素来显示三角形,那么问题就来了:
像素如何近似的表示一个三角形呢?
如前所说,像素是一个颜色均匀分布的正方形的小格子,那么如果遇到下面这种情况,如何用像素表示三角形?

一个简单的解决方法:采样(Sampling)
如何解释采样?比如我有一个函数f(x,y),在屏幕上的根据要求 ,比如隔一个点求一个f(x,y)的值,或者求一小块区域内的某一个点的作为这个区域的值,这就是采样。我们可以通过采样对函数离散化,如下,只求每一个整数点的输出,跳过小数。
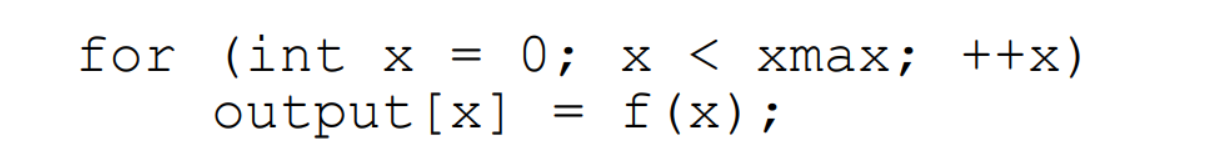
采样是图形学中的一种核心思想,可以对时间(1D),区域(2D),方向(2D),体积(3D)等进行采样。
用2D的采样方法来进行光栅化
对下面这个三角形进行采样:

将每一个像素中心作为采样点,如果该点在三角形内,就为这个像素添加上橙色,否则不添加。


上述用函数的实现就是定义一个二值函数: inside(tri,x,y)

然后对图像进行光栅化,就是用这个函数对图像进行采样,为1的区域设置为橙色,0的区域不上色。

如何判断该像素中心是否在三角形内部?
之前说过,运用向量的叉乘,按照顺时针或逆时针的方式,判断边向量和 该边向量的出发点到该点的向量 的叉乘是否都指向屏幕内或者屏幕外。若是,则点在在三角形内部,若不是,则点在三角形外部。

例如判断Q是否在三角形内部:
用(AB)表示A->B的向量。
(P2P1)×(P2Q) 得到的向量指向屏幕内,Q在(P2P1)的左边
(P1P0)×(P1Q) 得到的向量指向屏幕内,Q在(P0P1)的左边
(P0P2)×(P0Q) 得到的向量指向屏幕外,Q在(P0P2)的右边
所以Q在三角形的外部。
像素中心正好在三角形的边上的情况

不同的API中有不同的规定,也可以有你自己的规定。
采样的范围
对图像进行光栅化,有必要对整个图像进行采样吗?答案是否定的,我们用如下的一个包围盒(Bounding box),只对包围盒内部的像素进行采样,这样就减少了采样次数,增加了效率

光栅化中会出现的问题 - 锯齿
先对图像进行采样,得到了下面的结果,橙色的点的像素要染色

如果用上面的方法进行光栅化,那么最后得到的三角形就是这样的

这和我们想要的三角形相差太多,其并不光滑,棱角过多。所以就要对其进行抗锯齿操作。抗锯齿的内容下节课再说。