提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
参考:注意力机制
文章目录
- 前言
- 一、注意力机制
- 1.非参注意力池化层
- K(x-x~i~)的选择
- 2.参数化的注意力机制
- 3.小结
- 二、注意力分数
- 一维注意力分数
- 拓展到高纬度
- 1.加性的注意力
- 2.缩放点积注意力
- 3.小结
- 总结
前言
从心理学的角度上
- 动物需要在复杂环境下有效关注值得注意的点;
- 心理学框架:人类根据随意线索和不随意线索选择注意点
比如在一堆物品中,首先看到的是最显眼的一个物品,这叫不随意线索;再比如我想看书,然后我去找书,这叫随意线索。

一、注意力机制
- 卷积、全连接、池化层都只考虑不随意线索;
- 注意力机制则显示的考虑随意线索
- 随意线索被称之为查询(query);
- 每个输入是一个值(value)和不随意线索(key)的对;
- 通过注意力池化层使查询与键进行匹配,引导得出最匹配的值(感官输入)。

1.非参注意力池化层
- 给定数据(xi,yi),i=1,…,n,即key value pair,所有候选的东西;
- 平均池化是最简单的方案:f(x)=(y1+y2+…+yn)/n,x表示要查询的东西,不管要查询的是哪个y,直接做均值,比较粗暴;
- 更好的方案是Nadaraya-Watson核回归,K(x-xi)表示衡量x和xi距离的函数,对yi加权求和,即找到与x相近的xi的yi加权和,与x相近的xi的yi权值高,与x不相近的xi的yi权值高,权值高的yi的影响高于权值低的yi的影响;

K(x-xi)的选择
- 使用高斯核(正态分布)

那么有:

softmax(n)表示给n一个0到1之间的值,用来表示权重。
2.参数化的注意力机制
在下面的查询 𝑥 和键 𝑥𝑖 之间的距离乘以可学习参数W,W控制高斯分布的平滑程度。

此处的w是一维的,只有大小没有方向
3.小结
- 心理学认为人通过随意线索和不随意线索选择注意点;
- 注意力机制中,通过query(随意线索)和Key(不随意线索)来有偏向性的选择输入;
- 可以写成上一小节参数化的注意力机制的形式,其中softmax是注意力权重;
- 60年代就有非参数的注意力机制;
- 下面介绍多个不同的权重设计。
二、注意力分数
一维注意力分数

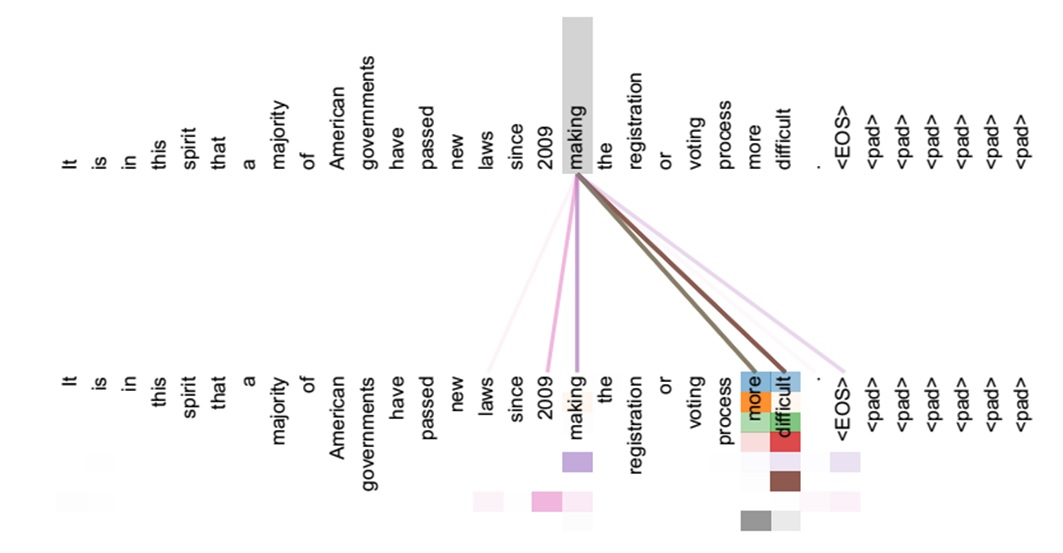
如下图所示,a表示注意力分数函数(Attention scoring function),将a计算出来的权重,跟Value做一个加权求和,得到最后的输出Output。

拓展到高纬度
上面所述的注意力机制的原理是一维层面的,现在将其扩展到高维,
- 假设query q∈Rq,q为长为q的向量,m对key-value(k1,v1),…,这里ki∈Rk,vi∈Rv,kivi也是向量;
- 注意力池化层:关键在于注意力分数函数怎么设计

下面提供两种注意力分数函数的设计思路
1.加性的注意力
- 有3个可学的参数:Wk、Wq、V(不是键值对中的值)可学习的参数是 𝐖q∈ℝh*q 、 𝐖k∈ℝh*k 和 𝐰𝑣∈ℝ ℎ


其中,Wk是一个hk的矩阵,Wq是一个hq的矩阵,v是长为h的向量,tanh表示激活函数,Wkk的结果为长为h的向量,Wqq的结果为长为h的向量,结果相加,将V的转置与激活后的相加的结果相乘,最后得到一个值。
- 等价于将query和key合并起来后放入一个隐藏大小为h输出大小为1的但隐藏层MLP,query和key可以是任意的长度。
2.缩放点积注意力
如果query和key都是同样的长度q,ki∈Rd,那么有:

除以根号d可以让注意力函数a的值不会太大
- 向量化版本
- a(Q,K)是一个n*m的矩阵,第i行表示第i个query和key的权重;
- f是一个n*m的矩阵,每i行表示第i个key对应的长度为v的向量。

3.小结
- 注意力分数是query和key的相似度,注意力权重是分数的softmax结果;
- 两种常见的分数计算:
1) 将query和key合并起来进入一个单输出单隐藏层的MLP;
2) 直接将query和key做内积,相当于query对key做投影,用投影表示他们的相似度。
data = pd.read_csv('https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())
该处使用的url网络请求的数据。
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。