汉诺塔问题
- 汉诺塔问题描述
- 算法步骤
- 三阶汉诺塔为例
- 函数递归
- 什么是递归
- 递归的两个必要条件
- 解决方法
- 代码演示
汉诺塔问题描述
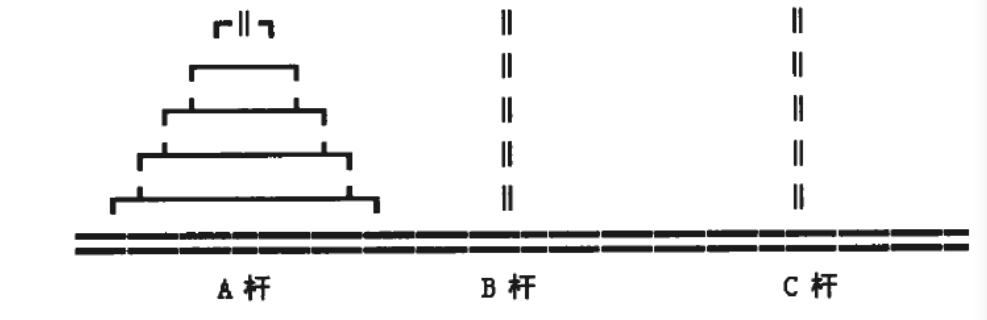
有一种被称为汉诺塔(Hanoi)的游戏,该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘。
游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。
操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
算法步骤
三阶汉诺塔为例
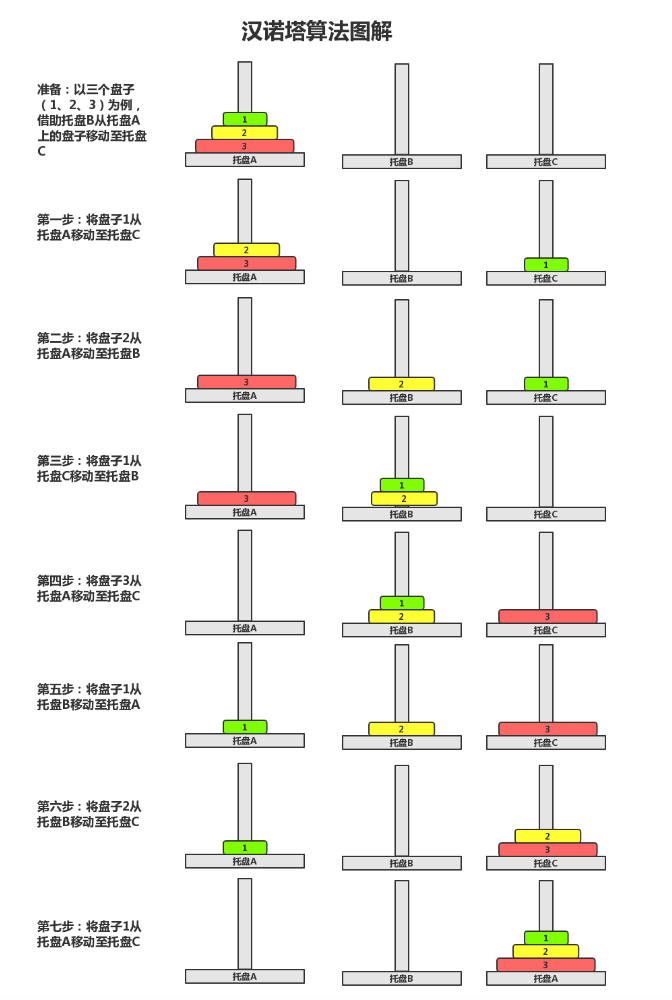
一共需要7步
函数递归
什么是递归
我的理解就是函数自己调用自己就是递归。
史上最简单的递归
//史上最简单的递归int main()
{//注意这里的递归是一个死递归//main 函数调用 main 函数main();return 0;
}
书中定义的递归概念:
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,
递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
递归的两个必要条件
(1)存在限制条件,当满足这个限制条件的时候,递归便不再继续。
(2)每次递归调用之后越来越接近这个限制条件。
解决方法
当n=1时,只要将编号为1的圆盘从柱子A直接移到柱子C上即可。
当n>1时,就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤:
(1) 将A柱子上的n-1个圆盘借助C柱子移到B柱子上;
(2) 把A柱子上剩下的一个圆盘从A柱子移到C柱子上;
(3) 最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。
需要移动的次数
当n = 1时,F(1) = 1
当n = 2时,F(2) = 2 * F(1) + 1
当n = 3时,F(3) = 2 * F(2) + 1
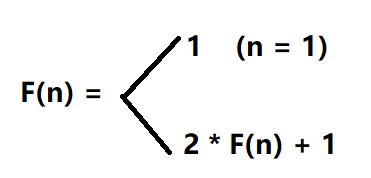
代码演示
//汉诺塔问题 递归代码实现
#include <stdio.h>//移动盘子的函数
void move(char x, char y)
{printf("%c->%c\n", x, y);
}//汉诺塔递归函数
void hanoi(char A, char B, char C, int n)
{//递归的第一要素 结束的条件是当只有一个盘子时 直接从A柱移动到C柱上去if (n == 1){move(A, C);}else{//递归的第二个必要的条件 大事化小 一步一步逼近结束的条件//先将n-1个盘子从A柱通过C柱移动到B柱hanoi(A, C, B, n - 1);//然后将最后剩下的那一个盘子 从A柱直接移动到C柱move(A, C);//最后将B柱上的n-1个盘子通过A柱移动到C柱hanoi(B, A, C, n - 1);}
}int main()
{int n = 0; //n用于记录一共有多少个盘子scanf("%d", &n);//汉诺塔问题解决函数hanoi('A', 'B', 'C', n);return 0;
}
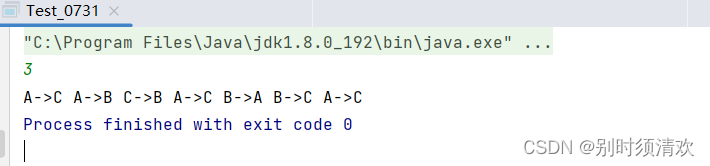
结果显示

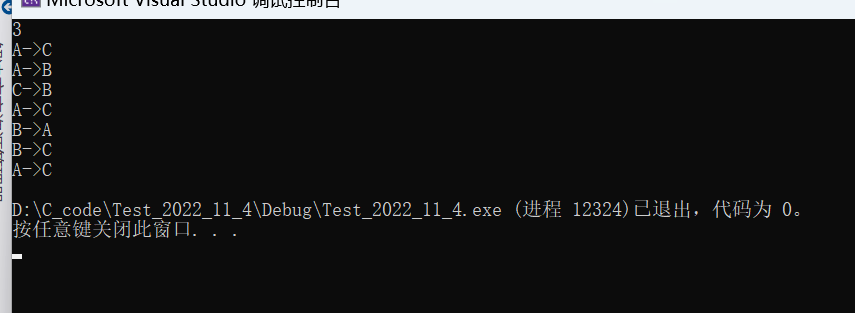
这里就是博主对汉诺塔问题的整体理解,希望能够给大家带来一些收获