标题 浅谈汉诺塔问题,以及对其递归的分析
首先谈谈汉诺塔这个问题,这个问题是印度的一个古老的传说。开天辟地的神勃拉玛在一个庙里留下了三根金刚石的棒,第一根上面套着64个圆的金片,最大的一个在底下,其余一个比一个小,依次叠上去,庙里的众僧不倦地把它们一个个地从这根棒搬到另一根棒上,规定可利用中间的一根棒作为帮助,但每次只能搬一个,而且大的不能放在小的上面。面对庞大的数字(移动圆片的次数)18446744073709551615,看来,众僧们耗尽毕生精力也不可能完成金片的移动。后来,这个传说就演变为汉诺塔游戏。
作为一个green hand,拿到这题的时候我是有些茫然的,感觉无从下手,没有什么思路。然后我就随手画了3个柱子,3个盘子。没一会就成功了,但这并没有真正的成功,因为我的这次成功是慢慢的尝试出来的。后来我就多画了几个盘子,慢慢尝试,总结其中的规律,经过一下午的探索,也算有了一点浅薄的心得,下面我就来谈谈。
很明显,这个问题需要用到递归才能解决,而用到递归的问题,往往可以使其简单化,把一个复杂的问题转化为一个个相似而简单的小问题。而这,也正是其中之一的难点,首先要想到怎么转化这个复杂的问题。经过一系列的尝试后,我发现,要想解决这个问题,你总是要把最大的盘子上的小盘子想办法移到中间的柱子上,然后再将最大的那个移到最后的一根柱子上,至此,也就发现了其中的共性点。
下面给出图示,以便理解
**
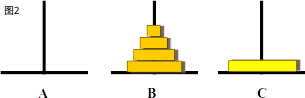

这其中最重要的一步就是一定要将最大的一个盘子移到c柱上,下面谈谈我对这一步重要性的理解。其实想到这时,我不禁想到了线性代数上行列式的计算,如果要计算一个4阶行列式,显然是很复杂的,但我们可以利用代数余子式将其转化为几个3阶行列式的和,这样就简便了运算。
这个问题中也是用到了同样的思想,当把最大的单独移到最后一个柱子上时,那样我们就不需要考虑那个盘子了,因为那个盘子是所有盘子中最大的,然它此时正在最下面,所以如图5个盘子的问题,当到图2那一步后,也就转化为4个盘子的问题.
此时也就成了这样
此时又可以转化一下思维,我们不妨将A,B,C三个柱子换下顺序,因为这样并不会影响结果。

此时5个盘子的问题就转化成4个盘子的问题了,以此方法类推,最后就可以解决汉诺塔的问题了。
以上是整个问题的算法,以及是如何想到的,接下来就是写程序了
void move(char c1, char c2);
void hannuo(int n, char x, char y, char z)
{if (n == 1)move(x, z); //递归截止条件else{hannuo(n - 1, x, z, y);//将 n-1个盘子先放到B座位上move(x, z);//将A座上地剩下的一个盘移动到C盘上hannuo(n - 1, y, x, z);//将n-1个盘从B座移动到C座上}
}
void move(char c1, char c2)
{printf("%c--->%c\n", c1, c2);
}int main()
{int n;printf("input your number");scanf("%d", &n);hannuo(n, 'a', 'b', 'c');return 0;
}
#下面来分析下这个代码里面的递归部分

然后我用代码运行了一下,验证了一下分析,与分析完全一致.