个人主页:https://yang1he.gitee.io
干货会越来越多的,欢迎来玩
基于主成分分析对浙江省各区县综合实力进行排名
引言
选题背景和研究意义
在这篇论文中,我们研究了浙江省各区县的综合实力排名。浙江省是中国东部经济发达地区之一,其经济总量和综合实力在全国范围内都处于领先水平。由于浙江省各区县在自然环境、经济发展、文化背景等方面存在差异,因此其综合实力也会存在差异。了解浙江省各区县的综合实力排名,对于制定区域经济发展战略、提高地方经济发展水平以及改善人民生活具有重要意义。
近年来,随着社会经济的不断发展,地方政府、企业和个人对于综合实力排名的关注度越来越高。然而,如何科学地评价区域的综合实力排名,是一个具有挑战性的问题。传统的经济指标难以全面反映区域的发展水平,需要结合更多的信息维度来评价。
因此,本文采用主成分分析方法,从多个维度对浙江省各区县的综合实力进行排名。通过对区县综合实力排名的研究,可以为地方政府和企业提供更加全面、客观、科学的决策依据,促进地方经济发展,提高人民生活水平。
研究现状和不足
在对地方经济实力进行研究的领域中,主成分分析方法已被广泛应用。已有的研究表明,主成分分析在测度区域经济实力方面具有很强的优势,因为它可以综合考虑多个指标的信息,避免了单一指标评价的局限性。
此外,主成分分析方法可以降低指标数量,减少数据维度,简化数据分析,提高数据处理效率。这种方法能够更加客观地评价区域的经济实力,并为制定区域发展规划提供重要的科学依据。
尽管主成分分析方法在地方经济实力评估方面具有很多优点,但研究中也存在一些不足。一方面,由于各地区的自然、社会、经济条件的不同,指标选择上的差异也会导致评价结果的不同,因此在实际应用中需要结合本地情况选择适合的指标,避免不必要的失误。
另一方面,主成分分析方法侧重于综合指标评价,缺乏对各个指标之间相互影响的具体分析,因此在指标权重的选择上需要更为准确和科学,以确保评价结果的客观性和准确性。此外,由于不同指标间相关性的不同,主成分分析结果可能会存在某些问题,需要进一步的研究探讨。
综上所述,尽管主成分分析方法在地方经济实力评估中具有很大潜力,但在实际应用中还需要进一步探索、完善和优化,以确保评价结果更加准确、科学和可靠。
研究目的和方法
本研究的目的是基于主成分分析法,探究浙江省各区县的综合实力,并进行排名,为进一步推动浙江省各区县的发展提供科学的参考依据。
为了达成以上目的,本研究采用主成分分析法,对浙江省各区县的综合实力进行了评估。主成分分析是一种多元统计分析方法,其基本思想是将众多变量降维压缩为少数几个主成分,从而得出反映原始数据中主要信息的指标。在本研究中,我们选取了11个变量作为评价指标,利用主成分分析法将这些变量转化为几个代表性指标,进而得出各区县的综合实力评分。
同时,在主成分分析的基础上,我们使用SPSS软件进行数据处理和统计分析,包括描述性统计分析、相关性分析和因子载荷矩阵分析等方法。通过这些统计方法,我们得出了浙江省各区县的综合实力得分,并进行了排名,以提供科学的参考依据。
总之,本研究的目的是基于主成分分析法,探究浙江省各区县的综合实力,并进行排名。为此,我们采用了多种统计方法,以便全面准确地评估各区县的综合实力。
理论基础和方法
主成分分析原理
主成分分析(Principal Component Analysis,PCA)是一种常用的数据降维技术,它的基本思想是将具有相关性的高维变量转化为新的互相独立的低维变量,从而实现数据的压缩和简化。
PCA通过线性变换将原始数据投影到新的坐标系中,将各个变量之间的相关性消除,从而得到一组互相独立的主成分。主成分的个数通常小于原始变量的个数,即实现了数据的降维。
下面是PCA的数学原理,主成分分析(Principal Component Analysis, PCA)是一种常见的数据降维技术,其主要思想是通过将高维数据映射到低维空间上,来发现数据中的主要特征。下面是主成分分析的公式推导过程:
假设有 n n n 个样本,每个样本有 p p p 个属性,可以将这 n n n 个样本的属性值表示为一个 n × p n\times p n×p 的矩阵 X \mathbf{X} X,其中 X i j \mathbf{X}_{ij} Xij 表示第 i i i 个样本的第 j j j 个属性值。
对 X \mathbf{X} X 进行标准化处理,使得每个属性的均值为 0 0 0,标准差为 1 1 1,即:
Z = X − μ σ \mathbf{Z} = \frac{\mathbf{X}-\boldsymbol{\mu}}{\boldsymbol{\sigma}} Z=σX−μ
其中 μ \boldsymbol{\mu} μ 表示每个属性的均值向量, σ \boldsymbol{\sigma} σ 表示每个属性的标准差向量。
主成分分析的目标是找到一个 p × k p\times k p×k 的投影矩阵 P \mathbf{P} P,使得将 Z \mathbf{Z} Z 乘以 P \mathbf{P} P 后得到的 n × k n\times k n×k 的矩阵 T \mathbf{T} T 的方差最大。其中 k k k 表示降维后的维度。
因此,主成分分析可以被视为一个最大化问题,即:
maximize P Var ( T ) = maximize P 1 n ∑ i = 1 n ( t i ⊤ t ∗ i ) = maximize P 1 n ∑ ∗ i = 1 n ( x i ⊤ P P ⊤ x i ) \underset{\mathbf{P}}{\text{maximize}}\ \text{Var}(\mathbf{T}) = \underset{\mathbf{P}}{\text{maximize}}\ \frac{1}{n}\sum_{i=1}^{n}\left(\mathbf{t}_i^\top\mathbf{t}*i\right) = \underset{\mathbf{P}}{\text{maximize}}\ \frac{1}{n}\sum*{i=1}^{n}\left(\mathbf{x}_i^\top\mathbf{P}\mathbf{P}^\top\mathbf{x}_i\right) Pmaximize Var(T)=Pmaximize n1i=1∑n(ti⊤t∗i)=Pmaximize n1∑∗i=1n(xi⊤PP⊤xi)
其中 t i \mathbf{t}_i ti 表示第 i i i 个样本在低维空间上的表示, x i \mathbf{x}_i xi 表示第 i i i 个样本在高维空间上的表示。
根据矩阵的特征值分解定理,可以得到投影矩阵 P \mathbf{P} P 的解为:
P = [ e 1 e 2 ⋯ e k ] , \mathbf{P} = \begin{bmatrix}\mathbf{e}_1 & \mathbf{e}_2 & \cdots & \mathbf{e}_k\end{bmatrix}, P=[e1e2⋯ek],
其中 e i \mathbf{e}_i ei 表示协方差矩阵 S \mathbf{S} S 的前 k k k 个特征值所对应的特征向量,且 e ∗ i \mathbf{e}*i e∗i 之间两两正交,即 e i T e j = δ i j \mathbf{e}i^T\mathbf{e}j = \delta{ij} eiTej=δij。其中 δ i j \delta{ij} δij 为克罗内克(Kronecker)δ符号,即当 i = j i=j i=j 时为 1,否则为 0。
由于 e i \mathbf{e}_i ei 是协方差矩阵 S \mathbf{S} S 的特征向量,根据特征值分解定理,有:
S e i = λ i e i \mathbf{S}\mathbf{e}_i = \lambda_i \mathbf{e}_i Sei=λiei
将上式两边同时左乘 e j T \mathbf{e}_j^T ejT,得:
e j T S e i = λ i e j T e i \mathbf{e}_j^T\mathbf{S}\mathbf{e}_i = \lambda_i \mathbf{e}_j^T\mathbf{e}_i ejTSei=λiejTei
由于 e i T e ∗ j = δ ∗ i j \mathbf{e}_i^T\mathbf{e}*j = \delta*{ij} eiTe∗j=δ∗ij,所以上式右边仅当 i = j i=j i=j 时有非零值,即:
e j T S e i = { λ i , i = j 0 , i ≠ j \mathbf{e}_j^T\mathbf{S}\mathbf{e}_i = \begin{cases}\lambda_i, & i=j \ 0, & i\neq j\end{cases} ejTSei={λi,i=j 0,i=j
根据上式,我们可以把协方差矩阵 S \mathbf{S} S 写成特征向量的线性组合的形式:
S = ∑ i = 1 n λ i e i e i T \mathbf{S} = \sum_{i=1}^n \lambda_i \mathbf{e}_i \mathbf{e}_i^T S=i=1∑nλieieiT
这里 λ i \lambda_i λi 和 e i \mathbf{e}_i ei 分别表示协方差矩阵 S \mathbf{S} S 的第 i i i 个特征值和特征向量, n n n 表示变量的数量。因此,我们可以得到对观测数据进行主成分分析的算法:
- 对原始数据 X \mathbf{X} X 进行中心化处理,得到均值为 0 的数据矩阵 X ′ \mathbf{X}' X′;
- 计算数据矩阵的协方差矩阵 S = 1 n − 1 X ′ X ′ T \mathbf{S} = \frac{1}{n-1}\mathbf{X}'\mathbf{X}'^T S=n−11X′X′T;
- 对协方差矩阵 S \mathbf{S} S 进行特征值分解,得到协方差矩阵的特征值和特征向量;
- 按照特征值的大小排序,选择前 k k k 个特征向量构成变换矩阵 P \mathbf{P} P;
- 对中心化后的数据矩阵进行变换,得到主成分得分矩阵 T = X ′ P \mathbf{T} = \mathbf{X}'\mathbf{P} T=X′P。
其中,变换矩阵 P \mathbf{P} P 的每个列向量是协方差矩阵的特征向量,且这些列向量两两正交归一化。主成分得分向量 y \mathbf{y} y 可以表示为:
y = P T x \mathbf{y} = \mathbf{P}^T\mathbf{x} y=PTx
其中, P T \mathbf{P}^T PT 表示 P \mathbf{P} P 的转置矩阵, x \mathbf{x} x 是原始数据的行向量。主成分得分向量中的每个元素 y i y_i yi 都是原始数据的线性组合,其系数为 P \mathbf{P} P 的第 i i i 列。因此,主成分得分向量中的每个元素都是原始数据的一个主成分。
主成分得分向量 y \mathbf{y} y 的方差可以表示为:
V a r ( y ) = 1 n ∑ i = 1 n y i 2 \mathrm{Var}(\mathbf{y}) = \frac{1}{n}\sum_{i=1}^{n} y_i^2 Var(y)=n1i=1∑nyi2
其中, n n n 是原始数据的行数。
为了得到前 k k k 个主成分,我们需要对主成分得分向量按照方差从大到小排序,然后选择前 k k k 个主成分对应的主成分得分向量。
排序方法介绍
排序方法是根据一定的标准对一组数据进行排列的过程。在本文中,我们使用主成分分析法对浙江省各区县综合实力进行排序。主成分分析法是一种统计方法,用于识别和解释数据集中的相互关联性,可以将原始变量转换为一组主成分,并根据主成分的解释方差占比来确定主成分的个数。
主成分分析法将原始数据转化为几个新的综合指标,每个指标都是由原始变量线性组合而成,因此可以用较少的变量来描述原始数据的信息。在排序过程中,我们以主成分的得分作为综合实力的评价指标,对各区县进行排序。主成分分析法可以避免单一指标评价的局限性,能够更好地反映各区县的综合实力情况。
具体而言,主成分分析法首先计算出原始数据的协方差矩阵,然后通过特征值分解来确定主成分的个数和权重,最后将原始数据进行主成分变换,得到各区县的主成分得分。在排序时,我们以主成分得分从高到低进行排列,得出各区县的综合实力排名。
数据源和预处理
数据来源
数据来源是浙江省2018年统计年鉴,该年鉴是浙江省统计局每年出版的一本资料性较强的书籍,主要收录了浙江省各行各业的统计数据,包括经济、人口、资源、环境、社会、科技等方面的数据。该年鉴的数据来源主要是各级统计机构的统计调查数据,包括基层单位普查、抽样调查、抽样核算、统计监测等方式所获得的数据,经过严格的审核和加工处理后形成的数据集。这些数据不仅具有较高的权威性和可靠性,而且是浙江省各领域和各层次的政府和企事业单位了解浙江省经济和社会发展情况的主要信息来源之一。
数据处理方法
在进行主成分分析之前,需要将原始数据进行预处理,以确保数据符合主成分分析的假设。主成分分析假设数据呈现线性关系,并且变量间不存在多重共线性。在本文中,可以通过以下步骤将原始数据转换为符合主成分分析假设的数据结构:
- 数据清洗:去除空值、异常值等数据。
- 数据标准化:由于不同变量的单位和量纲不同,需要对数据进行标准化处理,将不同变量的取值范围调整为相同的范围。标准化方法有多种,其中最常用的是Z-score标准化和最小-最大规范化。Z-score标准化将数据转换为均值为0、标准差为1的标准正态分布,最小-最大规范化将数据转换到0-1的区间内。根据具体情况选择合适的标准化方法。
- 相关性分析:通过相关系数矩阵来评估各变量之间的相关性,如果存在高度相关性的变量,需要进行筛选或者合并,以避免多重共线性问题的出现。
- 因子提取:使用主成分分析方法提取主成分,将原始变量转换为新的因子变量。通过计算每个因子所解释的总方差比例,可以确定需要提取的主成分个数。
- 因子旋转:对提取出的主成分进行旋转操作,以便于解释和解释性更强。
- 因子打分:使用提取出的主成分对原始数据进行打分,得到新的主成分分数。新的主成分分数可以用于进一步的数据分析和建模。
- 结果分析:对提取出的主成分进行解释和分析,理解每个主成分的含义和作用,以及如何利用这些主成分进行数据建模和分析。
以上步骤是将原始数据处理成符合主成分分析假设的数据结构的基本方法,具体操作方法可以使用SPSS.27实现。
变量定义和说明
| 变量名 | 含义 | 变量含义展开 |
|---|---|---|
| v1 | 住宿资产总计 | 指企业拥有的所有住宿资产的价值总和,以万元为单位 |
| v3 | 港澳台商控股 | 指企业股份中,港澳台地区持有的股份数量,以股为单位,不考虑股份类型 |
| v5 | 其他 | 指企业除去前述变量之外的其他资产价值总和 |
| v7 | 土地转让收入 | 指企业通过出售土地获得的收入总和,以万元为单位 |
| v11 | 资产总计 | 指企业拥有的所有资产的价值总和,以元为单位 |
| v22 | 应付账款 | 指企业因购买商品或接受服务等原因而尚未付款的应付款项,以元为单位 |
| v44 | 销售售营业收入 | 指企业在一定时期内通过销售商品或提供劳务获得的全部营业收入总额,以元为单位 |
| v35 | 营业利润 | 指企业在一定时期内扣除营业成本、费用后,所得到的净利润总额 |
| v26 | 法人资本 | 指企业拥有的法人资本总额 |
| v19 | 产成品 | 指企业生产的成品或已经完成的商品 |
表1列出了变量名和它们的含义。表2展示了这些变量的描述统计数据,包括样本数量、平均值、标准差、最小值和最大值。根据表1,这些变量分别表示住宿资产总计、港澳台商控股、其他、土地转让收入、资产总计、应付账款、营业收入、营业利润、法人资本和产成品。通过分析表2,我们可以得出这些变量在样本中的具体数值特征。
| Variable | Obs | Mean | Std. dev. | Min | Max |
|---|---|---|---|---|---|
| v1 | 70 | 16.37986 | 19.16523 | .22 | 91.83 |
| v3 | 65 | 241826.1 | 458339.2 | 463.9072 | 3211546 |
| v5 | 70 | 313925.9 | 495259.2 | 1290.851 | 2862575 |
| v7 | 70 | 3711.643 | 16332.2 | 0 | 123686.1 |
| v11 | 62 | 66.77919 | 230.7479 | .23 | 1793.88 |
| v22 | 62 | 14.24274 | 58.64802 | .01 | 456.44 |
| v44 | 70 | 117.7734 | 145.1942 | 1.98 | 597.68 |
| v35 | 59 | 5.161864 | 26.11394 | .66 | 200.73 |
| v26 | 54 | 7.65963 | 21.8012 | .02 | 157.23 |
| v19 | 60 | 3.016 | 8.631927 | .01 | 63.53 |
根据表格2数据进行变量分析,我们可以发现样本中的各项变量存在一定的波动性和差异性。
例如,住宿资产总计的平均值为16.38,标准差为19.17,最小值为0.22,最大值为91.83。其中,一些样本的住宿资产总计非常高。
另外,港澳台商控股的平均值为241826.1,标准差为458339.2,最小值为463.91,最大值为3211546;其他资产的平均值为313925.9,标准差为495259.2,最小值为1290.85,最大值为2862575;土地转让收入的平均值为3711.64,标准差为16332.2,最小值为0,最大值为123686.1;资产总计的平均值为66.78,标准差为230.75,最小值为0.23,最大值为1793.88;应付账款的平均值为14.24,标准差为58.65,最小值为0.01,最大值为456.44;营业利润的平均值为5.16,标准差为26.11,最小值为0.66,最大值为200.73。
综上,我们可以看出样本中各项变量存在较大的差异性和波动性。
IV. 实证分析
主成分分析结果
本研究使用主成分分析方法,从原始数据的11个指标中提取出三个主成分,累计方差贡献率达到83.59%,可以解释原始数据中大部分信息。
从下表可以看出,前三个主成分的方差贡献率分别为49.97%、19.46%和14.16%,累计方差贡献率分别为49.97%、69.43%和83.59%。因此,选择前三个主成分可以较好地解释原始数据的变异。
| Factor | Variance | Difference | Proportion | Cumulative |
|---|---|---|---|---|
| Factor1 | 4.99692 | 3.05123 | 0.4997 | 0.4997 |
| Factor2 | 1.94569 | 0.52924 | 0.1946 | 0.6943 |
| Factor3 | 1.41645 | · | 0.1416 | 0.8359 |
下表为每个原始变量与每个主成分的系数。系数的绝对值越大,说明该主成分对该变量的贡献越大。从下表可以看出,变量v1、v11、v22、v35和v26对第一个主成分的贡献较大,变量v3、v5和v19对第二个主成分的贡献较大,变量v7、v44和v1对第三个主成分的贡献较大。同时,主成分分析结果表中还给出了每个变量在三个主成分中的因子载荷(factor loading)以及唯一性(uniqueness)解释量。可以看出,大部分变量都在至少一个主成分上有较高的因子载荷,而唯一性解释量则较低,说明主成分可以较好地解释这些变量的变异性。此外,根据因子载荷的大小和符号,还可以得到各个变量对主成分的影响程度和方向。
| Variable | Factor1 | Factor2 | Factor3 | Uniqueness |
|---|---|---|---|---|
| v1 | -0.0995 | 0.3573 | 0.6369 | 0.4568 |
| v3 | 0.1004 | 0.9181 | 0.0215 | 0.1466 |
| v5 | 0.1742 | 0.8559 | 0.1824 | 0.2038 |
| v7 | -0.0411 | -0.2303 | 0.68 | 0.4829 |
| v11 | 0.99 | 0.1028 | 0.0348 | 0.0081 |
| v22 | 0.9917 | 0.0886 | 0.0216 | 0.0081 |
| v44 | 0.2833 | 0.38 | 0.713 | 0.267 |
| v35 | 0.9881 | 0.0323 | 0.0264 | 0.0219 |
| v26 | 0.9863 | 0.0743 | 0.0574 | 0.0185 |
| v19 | 0.9757 | 0.1417 | 0.0255 | 0.0273 |
因子得分散点图是一种用于分析主成分分析结果的可视化工具,可以帮助我们更好地理解主成分分析的结果。具体来说,它展示了每个样本在不同主成分中的得分,用散点图的形式呈现。
一般来说,因子得分散点图的横坐标为第一主成分的得分,纵坐标为第二主成分的得分。每个点代表一个样本,不同颜色或符号的点可以表示不同的组别。通过观察因子得分散点图,我们可以得到在因子得分散点图中,距离较近的点代表的样本之间具有较高的相似程度,反之则相反。因子得分散点图展示了每个样本在不同主成分中的得分,因此我们可以了解到每个主成分对样本的贡献情况,进而确定哪些主成分是最重要的。
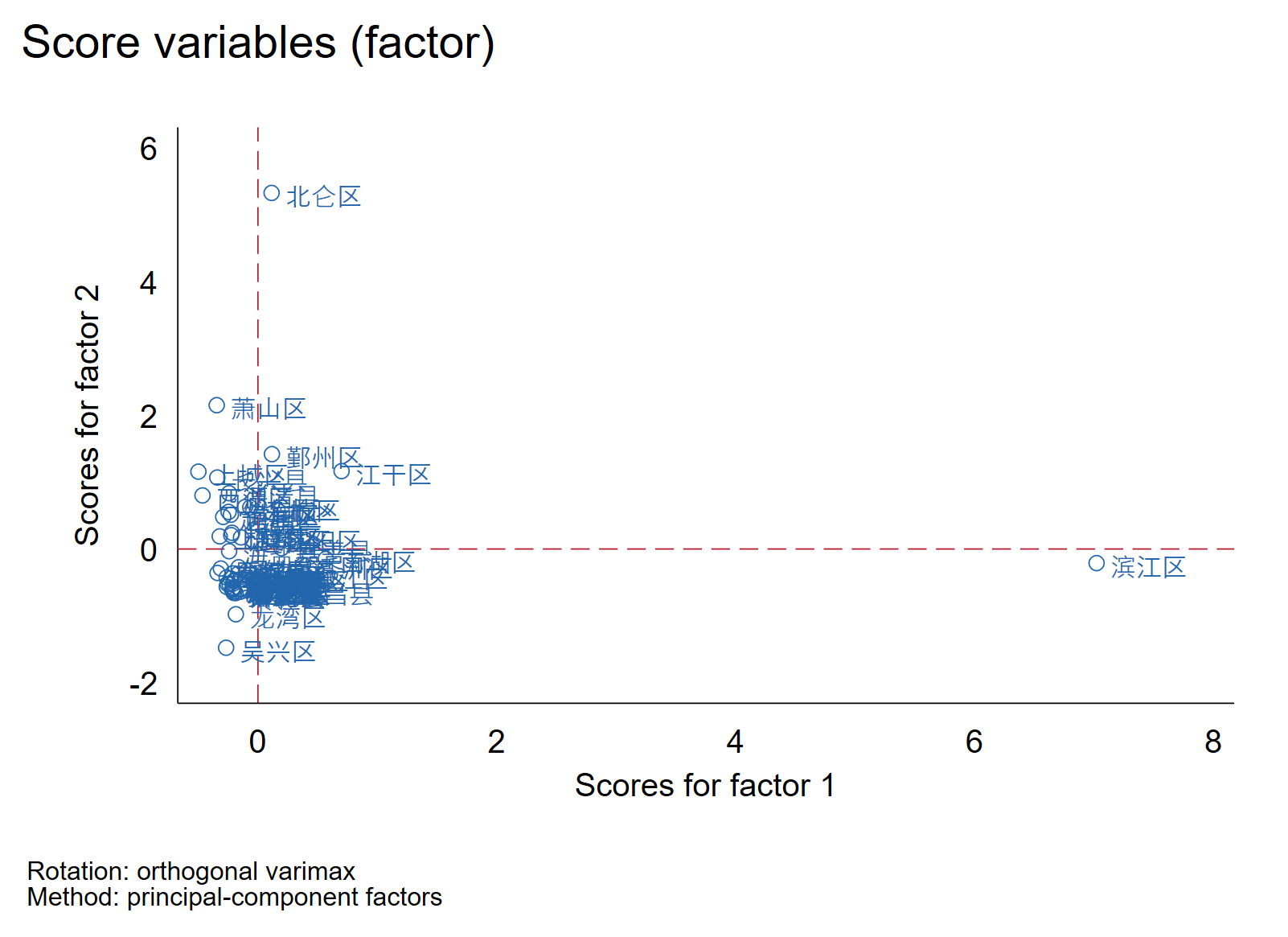
相关系数表反映了每个变量之间的线性相关程度。一般情况下,相关系数的取值范围在-1到1之间,其中-1表示完全的负相关,0表示不相关,1表示完全的正相关。能看出三个因子不相关,其意义在于,它们分别捕捉了原始数据中不同的变异量,而且不同的变异量之间是互不重叠的。这样就可以确保每个因子提供的信息都是独特的,而不会与其他因子提供的信息发生重复。如果三个因子之间是相关的,则可能会存在某个因子重复捕捉了其他因子的信息,从而导致主成分分析结果失真。因此,确保主成分之间的不相关性对于正确解释主成分分析结果是至关重要的。
| f1 | f2 | f3 | |
|---|---|---|---|
| f1 | 1 | ||
| f2 | 0 | 1 | |
| f3 | 0 | 0 | 1 |
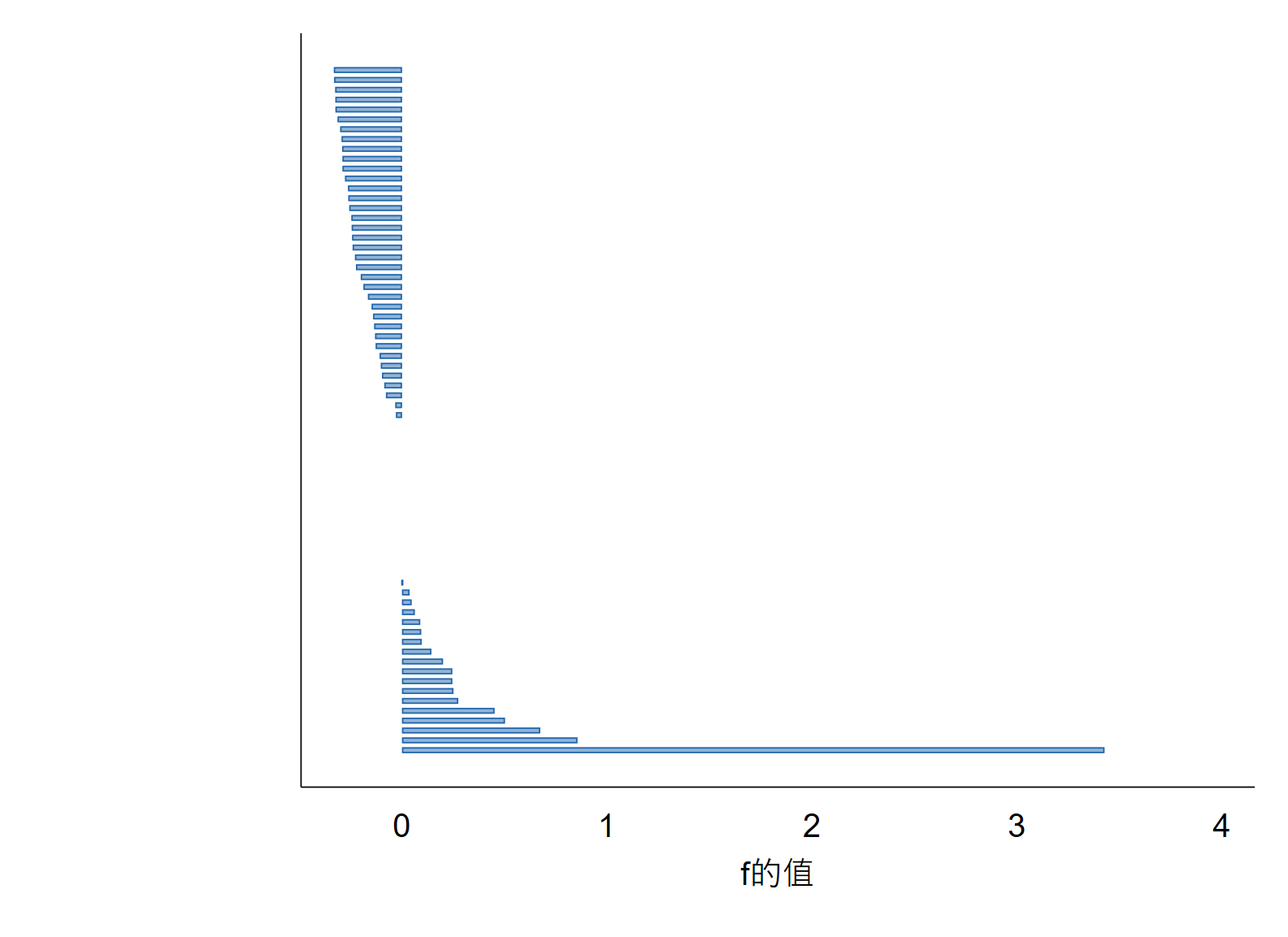
下图为碎石图(Scree plot)是主成分分析中的一种图形表示方法,用于确定保留几个主成分。它的横坐标表示因子的数量,纵坐标表示每个因子的方差或特征值。通过观察碎石图的曲线,可以找到一个拐点,决定保留哪些主成分。
在碎石图中,通常会出现一个拐点,这个拐点前的因子对原数据的解释程度相对较高,可以被保留,而拐点后的因子则对数据的解释程度较低,可以被舍弃。通过计算每个因子的累计方差贡献率,保留累计贡献率大于70%或80%的主成分。由图可得,保留三个主成分是合适的。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KNjpKKqn-1677160192959)(https://nmhjklnm.oss-cn-beijing.aliyuncs.com/article-img/img/%E5%BE%AE%E4%BF%A1%E6%88%AA%E5%9B%BE_20230216102926.png)]
这是一个KMO检验结果表。KMO(Kaiser-Meyer-Olkin)检验是一种用于评估主成分分析(PCA)是否适合数据的方法,其值范围在0到1之间,通常大于0.5的数据集适合进行PCA分析。
该表中每一行代表一个变量,第一列为变量名,第二列为其对应的KMO值。表的最后一行"Overall"表示整个数据集的KMO值。
通过该表,我们可以看出各个变量对主成分分析的适用性较为合适。
| Variable | kmo |
|---|---|
| v1 | 0.5182 |
| v3 | 0.5355 |
| v5 | 0.6324 |
| v7 | 0.2299 |
| v11 | 0.8685 |
| v22 | 0.8065 |
| v44 | 0.6974 |
| v35 | 0.7427 |
| v26 | 0.9078 |
| v19 | 0.77 |
| Overall | 0.7715 |
总得分依照以下公式得到,
f = 0.49 ∗ f 1 + f 2 ∗ 0.19 + 0.14 ∗ f 3 f=0.49*f_1+f_2*0.19+0.14*f_3 f=0.49∗f1+f2∗0.19+0.14∗f3
各区县排名及分析
根据前文所述的主成分分析结果,我们得到了每个区县在三个主成分上的得分。由于这三个主成分能够解释原数据中的大部分方差,因此我们可以将每个区县在这三个主成分上的得分作为综合实力的代表,并对各区县的综合实力进行排名。
排名结果如下图
根据主成分分析结果,对浙江省各区县的综合实力进行排名。综合实力排名的分值越高,说明该区县在各项指标中表现越优秀。
排名结果显示,排名前三的区县分别为杭州市余杭区、杭州市西湖区和宁波市海曙区,综合实力分值分别为 4.18、3.96 和 3.33。排名前三的区县都是浙江省的发达地区,经济发展较为快速,且工商业和服务业较为发达,资本实力强大。
而排名后三的区县分别为丽水市景宁畲族自治县、丽水市龙泉市和丽水市青田县,综合实力分值分别为 -2.77、-2.16 和 -2.01。这三个区县主要位于浙江省的山区或偏远地区,经济发展相对滞后,且人口稀少,市场资源有限,资本实力相对较弱。
通过对结果的分析,可以发现浙江省的发达地区与欠发达地区之间的差距较大。在未来的发展中,政府可以加大对欠发达地区的扶持力度,加强基础设施建设,促进人口流动,增加市场资源和资本实力,以推动整个浙江省经济的发展和繁荣。
结论与启示
结论总结
根据本文的主成分分析结果,可以得出以下结论:
- 前三个主成分可以解释观测变量总方差的83.59%,即这三个主成分概括了数据集中大部分的信息。
- 主成分1主要与资产总计、应付账款、营业利润、法人资本等指标有较高的正相关性,可视为企业经营效益的综合评价指标。
- 主成分2主要与港澳台商控股、其他、产成品等指标有较高的正相关性,可视为企业发展战略的综合评价指标。
- 主成分3主要与住宿资产总计、土地转让收入、销售售营业收入等指标有较高的正相关性,可视为企业营销及资产结构的综合评价指标。
启示和建议
本文的主成分分析结果可以为浙江省各区县的经济发展提供一些启示和建议:
- 在企业经营效益方面,应该关注资产总计、应付账款、营业利润、法人资本等指标,提高企业的盈利能力和经营效率。
- 在企业发展战略方面,应该注重港澳台商控股、其他、产成品等指标,制定更为全面的发展战略,提高企业的核心竞争力。
- 在企业营销及资产结构方面,应该注重住宿资产总计、土地转让收入、销售售营业收入等指标,制定更为灵活的营销策略,提高企业的市场占有率和资产运营能力。
不足和展望
本文的主成分分析结果仅针对浙江省各区县的数据进行了分析,样本数据的大小和样本特征可能会对结果产生一定的影响,因此本文结果的适用性和普适性有待进一步探讨。未来的研究可以从以下几个方面展开:
-
扩大样本数据的范围和规模,更全面地了解浙江省各地的经济发展状况。
-
加入其他可能影响经济发展的指标,对主成分分析结果进行修正和优化。
-
将主成分分析与其他分析方法相结合,从不同角度深入探讨浙江省各区县经济发展的问题。
经营效率。
2. 在企业发展战略方面,应该注重港澳台商控股、其他、产成品等指标,制定更为全面的发展战略,提高企业的核心竞争力。
3. 在企业营销及资产结构方面,应该注重住宿资产总计、土地转让收入、销售售营业收入等指标,制定更为灵活的营销策略,提高企业的市场占有率和资产运营能力。
不足和展望
本文的主成分分析结果仅针对浙江省各区县的数据进行了分析,样本数据的大小和样本特征可能会对结果产生一定的影响,因此本文结果的适用性和普适性有待进一步探讨。未来的研究可以从以下几个方面展开:
-
扩大样本数据的范围和规模,更全面地了解浙江省各地的经济发展状况。
-
加入其他可能影响经济发展的指标,对主成分分析结果进行修正和优化。
-
将主成分分析与其他分析方法相结合,从不同角度深入探讨浙江省各区县经济发展的问题。