对于只有一个未知量的,通常是把未知量替换为x。令等式一边为0,然后把另一边当作F'(x),然后找原函数。在写解题过程时,不写如何求得F(x)的,直接设F(x),然后证明F(x)符合某一种中值定理。
例1:f(x),g(x)在[a,b]上连续,(a,b)上可导,g'(x)不等于0,证明

把式子中未知量替换为x得到

所以求得F(x)=f(a)g(x)+f(x)g(b)-f(x)g(x)
解:设F(x)=f(a)g(x)+f(x)g(b)-f(x)g(x),当x=a或b时,F(x)=f(a)g(b)。则根据中值定理可知,存在ξ属于(a,b)使得F'(x)等于0,又g'(x)不等于0,所以可以求得原式
有时,想要找出原函数,还有加上一个再减去一个项
例2:f(x)和g(x)在[a,b]上连续,(a,b)上可导,f(a)=g(b)=0,g'(x)<0。证明存在ξ属于(a,b)使得

根据思路,代入x后得到

这个等式左边当作F'(x),很难求出原函数,但以左边那一项为例,把他当作f(x)的导数乘以一个积分,则可以把它看作是左导右不导,加上左不导右导的那一项即可获得原函数。同样,右边的项也可以做相同处理,而且左右两项所要相加的刚好为相反数,则式子可以化为
![]()
原函数为
![]()
解:设
![]()
则F(a)=F(b)=0,根据罗尔中值定理可以得到

又因为g(b)=0,g'(x)<0,所以在(a,b)上,g(x)>0,所以式子可以化为

但这只是一般情况,有的时候,要利用柯西中值定理,此时要找到两个辅助函数
例3:f(x)在[1,2]上连续,在(1,2)内可导,且f(x)!=0,证明,存在ξ属于(1,2)使得

解:令h(x)=lnx

则根据柯西中值定理可得到原式



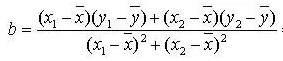






![[前言] 实现一个Android电子书阅读APP](http://images2015.cnblogs.com/blog/901197/201703/901197-20170304093408454-908789768.png)