地图符号作为表现地理空间中各种实在物体和相关现象的图像化表示方法,已逐渐成为GIS(ge-ographicinformationsystem,地理信息系统)系统和现代地图学中的研究热点之一,尤其是在电子海图系统研制过程中,其符号表达的好坏将直接影响系统的性能.根据符号在地图上的表现方式不同,可以将符号大体上划分为点状符号、线状符号以及面状符号3个大类.其中,由于线状符号的基本构成单元是点状符号,而且面状符号由线状符号构成;因此,线状符号作为承上启下的连接符号类被广泛使用.与此同时,线状符号也是地图符号中最复杂的一个类.线状符号一般由基本图元组成,基本图元可以是直线、折线、多边形以及各种简单图形.这些基本图元按照一定的排列组合方式绘制或填充就成为线状符号.
1.线状符号的基本概念
1.1.线状符号的分类
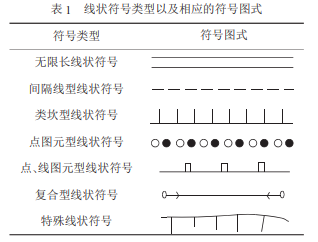
根据线状要素的构成特点以及实际绘制的需要可以将线状要素分成下列几类:
1)无限长线状符号:其特点是线状符号中没有间隔,可以看成是一个整体的线状符号单元.它是线状符号中最简单的一类.
2)间隔线型线状符号:此类符号是由一定长度的短线和线与线之间的有效空白通过有规律的拼接组成的线状符号.
3)类坎型线状符号:此类符号由定位线以及与定位线有一定角度的短线循环拼接而成.由于坎类线状要素属于其类且应用最为普遍,故称其为类坎型线状符号.
4)点图元型线状符号:此类符号的基本图元为点状要素,按照一定的顺序与有效空白连接而成.
5)点、线图元型线状符号:此类符号的基本图元为点状、线状要素,按照一定的顺序与有效空白连接而成.
6)复合型线状符号.这类符号是由上述几类符号组合而成.
7)特殊线状符号.这类符号是非规则符号,如陡崖、石滩等.各线状符号类型及相应符号图式如表1所示.
1.2.线状符号的可分解性与不可分解性
1)线状符号的可分解性.线状符号的可分解性是指线状符号的每一个图元都可由几个最基本的要素表示,这些要素按照一定的方式在线状符号定位线的串接下形成一个循环图元;所以一个线状符号可以由通过图元分解的线状要素组成,几乎所有的规则线状符号都是可分解的.
2)线状符号的不可分解性.线状符号的不可分解性是指线状符号中组成要素的单元或者排列顺序是随机的、没有规律的,所以不能把线状符号分解为基本图元.在绘制过程中只能把线状符号看成一个整体来进行绘制.一般不可分解的线状符号都是非规则的.如果要使符号单元分解后能优化配置,而且新组合后能达到较好的视觉要求,可以这样处理分解后的相互依赖的线状符号:一是直接优化配置,并将图案单元的每个定位点记录下来;二是根据它所依赖的线状符号的图案单元的定位点和它们的空间关系,求得它的图案单元在定位线上的配置坐标.故每种基本线状符号都应该有2种配置算法:根据其他图案单元的定位点和相对位置进行配置;单独按配置要求进行优化处理,记录每个图案单元的定位点坐标.线状符号的分解性与不可分解性是相对的.有些规则符号在优化配置的情况下是不能直接分解的,但若把它们的相对位置考虑进去就能进行分解;不规则线状符号一般不能分解,但若能找到符号单元和排列方式的变化规律,从理论上讲还是能进行分解的.
2.以视觉变量为主要成员的线状符号数据结构
2.1.视觉变量
虽然线状符号都可以分解为基本图元,但是这些基本图元之间是有差别的.这些能引起人们视觉差别的最基本的图形和色彩的变化因素叫做视觉变量或图形变量,也叫可视化变量.视觉变量直接关系到线状符号的形象特点.线状符号之间的差别就是因为它们之间一个或者多个视觉变量之间存在差别.
在一般情况下,图形由6个基本的视觉变量组成:形状、尺寸、颜色、密度、方向和明度.从线型符号基本组成要素图案的结构角度来说,线状符号可以用不同的形状、不同的尺寸、不同的颜色、不同的密度、不同的方向以及不同的明度和位置来区分各种不同线状地理事物的分布、质量、数量等特征,使得图形更具有表现力.
2.2.线状符号图元的数据结构
线状符号结构的不同决定了线状符号的不同;构成符号的基本线型由形状决定,形状变量的差别是线状符号表现在视觉上最重要的差别;密度、尺寸、位置是每个待配置符号参与绘制及其相关运算的最基本的视觉变量;在少数线状符号(如坎符号的堤岸)中,方向也作为一个参数参与运算;而每个线状符号显示、输出的色彩是由颜色、明度等视觉变量控制的.如果是单线符号,其颜色变化确定视觉效果;而当其宽度增加到一定程度时就要同时考虑亮度的变化.
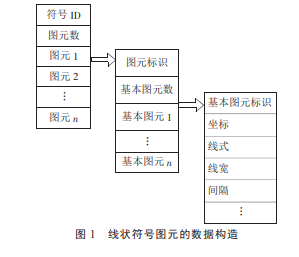
由此可以根据视觉变量定义一个基本线型的图案单元(只含单一的图元)的数据构造.图案单元信息={坐标,线式,线宽,间隔,偏移量,笔颜色,填充否,刷子颜色……}.坐标表示符号在地图坐标系中的位置;线式主要表现图元中线状要素的线型;线宽代表线状要素的宽度;间隔是指2个图元间沿定位线的相隔长度;偏移量是指图元与定位线之间的夹角,竖线的夹角为90°,横线的夹角为零;笔的颜色为RGB(红、绿、蓝)型;如果填充则考虑刷子的颜色,一般在有宽度的直线段(即矩形,多边形等)、圆等情况下才用到.
由于线状符号可能由多个不同种类的基本图元交替组成,因此可以由图1形象、直观地表达一个线状符号图元构造的数据构造情况.
3.线状符号拐点的基本处理方法
拐角点问题是由基本图元在拐点处绘制不当产生的,因为在循环配置时,基本图元可能跨越原有的定位线而引发在多个定位线上绘制的问题.根据不同类型线状符号在拐点处的表现形式不同,可以把拐点问题大致分为3个种类.
1)单一基本图元线状符号的拐点问题
此类符号的定位线可以在符号上,也可以在符号中,如图2(a)、2(b)显示此类符号在拐角处的问题.
对于图2(a)和2(b)中的问题,这里提出断点几何线状填充方法:
规定正方向,判断出现拐角点问题的部分相对于定位线的位置,即位于定位线拐角的内部还是外部,设定位线的夹角在0~180°之间,则判定方法如图3所示.
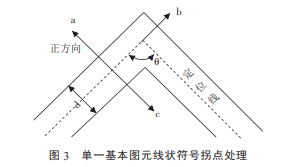
由向量乘积判定角度范围a軆×b軋<0,则需要在断点处补接线段的长度应为d′=d/sinθ+d·cotθ;若b軋×c軆>0,则需要在断点处补接线段的长度应为d′=d/sinθ.此处d指线状符号边界到定位线的距离.
对于在内部的拐点问题也需要先判断两定位线的夹角θ,若b軋×c軆<0,则需要在断点处擦除线段的长度应为d′=d/sinθ+d·cotθ;若b軋×c軆>0,则需要在断点处擦除线段的长度应为d′=d/sinθ.此处d指线状符号边界到定位线的距离.
优化后的符号图2(c)和图2(d)所示,可见优化后的线状符号有效地解决了拐点问题.
2)多基本图元线状符号的拐点问题
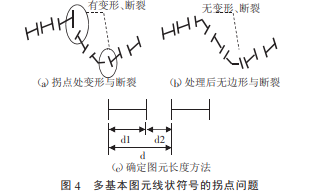
在通常情况下,对此类符号的绘制一般只考虑了定位线的起点和终点应采取的处理,而在定位线变化趋势较明显的拐点处可能出现基本图元断裂、错开、自交等严重变形的情况.如图4(a)所示.
这里提出了循环配置图元方法解决这个问题:在通常情况下,对此类符号的绘制应首先设定其图元的主要基本图元和次要基本图元.主要基本图元是指在拐点处绘制此基本图元可以保证符号的可连续性以及美观性,不给人以断裂或者不舒适的感觉的图元.次要基本图元可以辅助主要基本图元构成线状符号图元从而正确地显示该线状符号.具体的处理方法如下:
①将符号的图元划分为主要基本图元和次要基本图元.确定主要基本图元长度d1、次要基本图元长度d2、以及图元总长度d,如图4(c)所示.
②在每个拐点处把拐点作为主要基本图元的中点,并在拐点前后确定拐点图元的长度.
③设两拐点之间的距离为S,拐点图元在此部分的长度为d′,则可算出此长度线状符号绘制的图元数i以及剩余长度Δd.
④若Δdd1/2,则需要确定一个阈值长度δ,若δ>d/i,则将剩余长度Δd平均分给剩余图元,若δ通过上述方法优化后的符号如图4(b)所示,可见优化后的符号有效地解决了拐角处图像的严重变形问题;但在实际运行中可能由于处理方式的复杂性造成系统利用率高,绘制速度减慢等实际问题.
3)多基本图元填充线状符号的拐点问题
此类符号可以分解为上述2种方法的综合.其中,首先绘制封闭的线状填充区域及其边界线,线状填充区域及其边界线可以看做单一基本图元线状符号;其次绘制填充单元,填充单元即可看做多基本图元线状符号的图元要素.在实际中,充分利用上述2种拐点处理方法处理拐点,从而解决多基本图元填充线状符号的拐点问题.
4.结束语
通过对线状符号进行具体分析讨论,总结了线状符号的分类,针对线状符号在拐点处容易出现交叉、断裂、空白等失真现象,设计了以视觉变量为主要成员的线状符号数据结构,同时提出了断点几何线状填充以及循环配置图元方法,对线型符号的绘制进行了优化,使其在拐点处的绘制更加简洁、美观,因此具有一定的实际意义. 参考文章:电子海图、AIS、雷达