前面几章其实已经把基础的Latex中文文本写的差不多了。这一章节针对我论文中用到的数学公式写一些心得。
数学公式
通常理工科写论文,少不了数学公式。在公式上,我个人认为相比word,latex还是有非常大的优势。
行内公式
行内公式通常用一对$来表示,例如:
行内公式:$x_2+y_2=1$
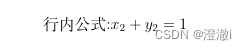
不过通常我们涉及到公式,在论文中都要进行标注,即要标记这是第几个公式等等。
这种情况一般用到行间公式。
行间公式
行间公式通常用两对$来表示,例如:
行间公式:$$x_2+y_2=1$$
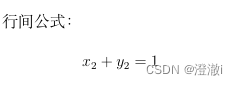
但是这里我们发现公式并没有标号,这时候需要用到环境这一词。
数学环境
equation
比较正规的公式写法,后面都是有数学公式的标号。这时候需要用到环境\begin{equation}
数学环境:\begin{equation}y=a_0+a_1x+a_2x^2+...+a_nx^n\label{1}\end{equation}
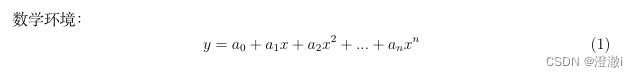
这里需要注意的是,使用数学环境,在数学的环境中,不需要使用$来表示这是数学公式。
上述代码段中,使用了\label{}的方式,对公式进行了标号。
gather
equation适用于单公式情况,这个环境直接翻译也就是等式的意思嘛,所以也就是一个等式的意思。
如果要一次性多写几个,那需要用到gather环境。使用gather环境需要用到\usepackage{amsmath}
\begin{gather}x+y=2\\x-y=-4
\end{gather}

这里我的公式是自动居中排版,同时每一个公示自动编号。此数学环境适用于一次性写多个公式。如果不想编号,只需要在gather后面加*
cases
如果我想将上述的两个方程放到一个方程组进行编号,这时候需要用到cases环境。使用cases环境最好搭配上equation环境使用,具体情况如下所示。
\begin{equation}\begin{cases}x+y=2\\x-y=-4\end{cases}
\end{equation}

这里会发现我们的标号是(3),所以可知道,使用数学环境编写的cases公式,会自带编号。
如果我们不使用equation环境,单独使用cases环境进行书写,会报错!。原因在于cases是数学的环境,所以必须作为数学公式使用,如果不放在环境里面,需要我们使用一对$作为数学公式的声明。
同时,使用$符号的数学与公式,是不会自动编号的
$$\begin{cases}x+y=2\\x-y=-4
\end{cases}$$
{ x + y = 2 x − y = − 4 \begin{cases} x+y=2\\ x-y=-4 \end{cases} {x+y=2x−y=−4
Latex数学公式的常用写法
刚才举例的情况中,以及涉及到了一些数学公式的写法。下面列举一些常用的写法。
上下标
上标用
^
下标用_
\begin{equation}y=a^0+a^1+a^2+a^3+a^4+...+a^n\label{1}
\end{equation}
\begin{equation}y=a_0+a_1x+a_2x^2+...+a_nx^n\label{2}
\end{equation}
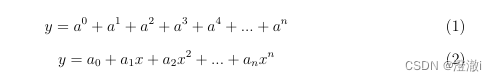
这里所使用的数学环境最好放一个数学公式,不然后面对公式进行标号会出现问题。
这两个例子就非常清晰的展示如何自己手写简单的上下标公式。
分数
\frac{分子}{分母}
$$f(\sigma)=\frac{1}{\sigma}$$
f ( σ ) = 1 σ f(\sigma)=\frac{1}{\sigma} f(σ)=σ1
这里我用到了希腊字母,这个可以参考上一章节的字母介绍。
积分
不定积分的写法是使用\int{被积函数}{积分单元}
定积分的写法是使用\int_{下限}^{上限}{被积函数}{积分单元}
我这里添加{}是为了大家能够更好的看清自己写的公式,也可以不添加。一旦公式复杂,不添加中括号真的很难看懂。
$$\int{f(x)}{dx}$$ %(1)
$$\int_1^2 f(x)\,{dx} $$ %(2)
$$\int_{-\infty}^{+\infty}f(x){dx} $$ %(3)
$$ \int \!\!\!\!\! \int_D f(x,y)\,dx\,dy$$ %(4)
$$\int\int_D f(x,y)\,dx\,dy $$ %(5)
$$\int \!\!\!\!\! \int \!\!\!\!\! \int_\Omega f(x,y,z)\,dx\,dy\,dz $$ %(6)
∫ f ( x ) d x ( 1 ) \int{f(x)}{dx}\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(1) ∫f(x)dx(1)
∫ 1 2 f ( x ) d x ( 2 ) \int_1^2 f(x)\,{dx} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(2) ∫12f(x)dx(2)
∫ − ∞ + ∞ f ( x ) d x ( 3 ) \int_{-\infty}^{+\infty}f(x){dx} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(3) ∫−∞+∞f(x)dx(3)
∫ ∫ D f ( x , y ) d x d y ( 4 ) \int \!\!\!\!\! \int_D f(x,y)\,dx\,dy\quad\quad\quad\quad\quad\quad\quad\quad\quad(4) ∫∫Df(x,y)dxdy(4)
∫ ∫ D f ( x , y ) d x d y ( 5 ) \int\int_D f(x,y)\,dx\,dy \quad\quad\quad\quad\quad\quad\quad\quad\quad(5) ∫∫Df(x,y)dxdy(5)
∫ ∫ ∫ Ω f ( x , y , z ) d x d y d z ( 6 ) \int \!\!\!\!\! \int \!\!\!\!\! \int_\Omega f(x,y,z)\,dx\,dy\,dz \quad\quad\quad\quad\quad\quad\quad\quad(6) ∫∫∫Ωf(x,y,z)dxdydz(6)
现在针对我前面举的例子进行阐述。
(1)(2)是常规的积分。(3)中 ∞ \infty ∞的写法是通过\infty来进行书写,如果想要 + ∞ +\infty +∞或者 − ∞ -\infty −∞,只需要在\infty前面添加+或者-即可。
代码中还出现了\,以及\!,前者是在公式中充当空格的作用,后者是缩短空格的作用。具体缩短多少单位字符,我没有具体研究过,只知道具体用法。如果网友感兴趣可以自己参考互联网。
接下来是多重积分的阐述。大家可以参考(4)(5)(6),我们看代码会发现其实\int只不过是一个 ∫ \int ∫符号罢了。所以其实我们写Latex的数学公式的时候完全可以当做搭积木的方式来写。需要什么符号就打什么符号。一个一个去凑即可。要上标就^{}下标就_{},积分就\int,符号就找对应表:\omega: ω \omega ω
极限
极限用到的\lim,依照刚才讲的搭积木的方式进行举例:
\lim_{变量 \to 趋向目标}{要求极限的表达式}
$$\lim_{x \to 0} \frac{x^2 +x^3}{x^2 +x^4}$$
lim x → 0 x 2 + x 3 x 2 + x 4 \lim_{x \to 0} \frac{x^2 +x^3}{x^2 +x^4} x→0limx2+x4x2+x3
针对某一项(上标或者下标这种),如果本身也是复合项,那最好用{}
更多的数学公式写法,可以参考互联网。
大招
最后,放个大招。
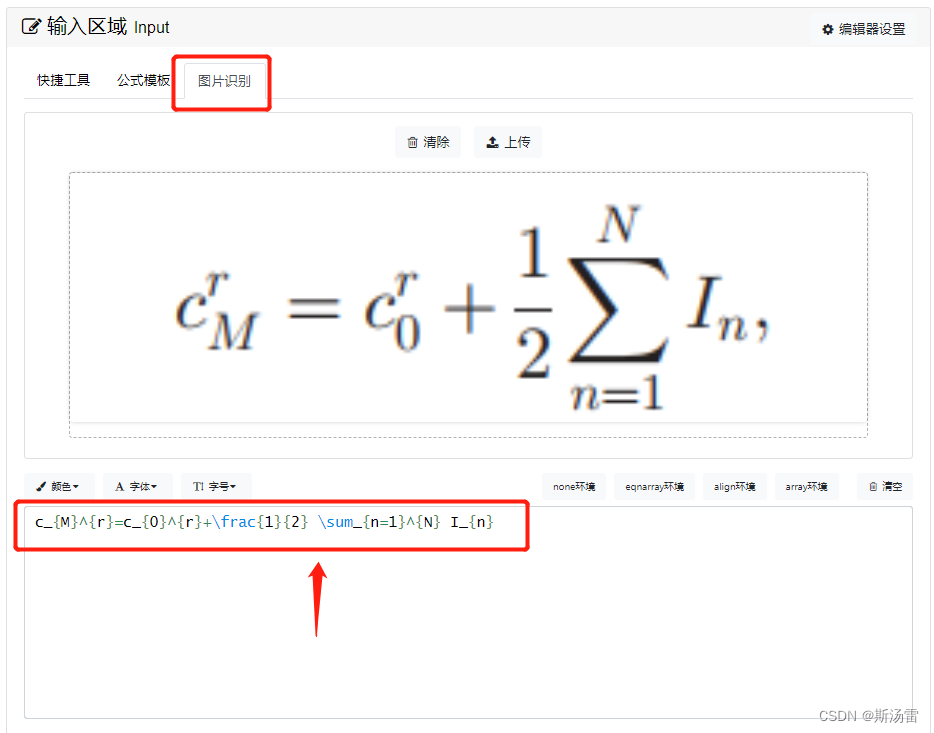
我一般写公式:简单的可以通过上述自己写。太多太复杂的,比如:
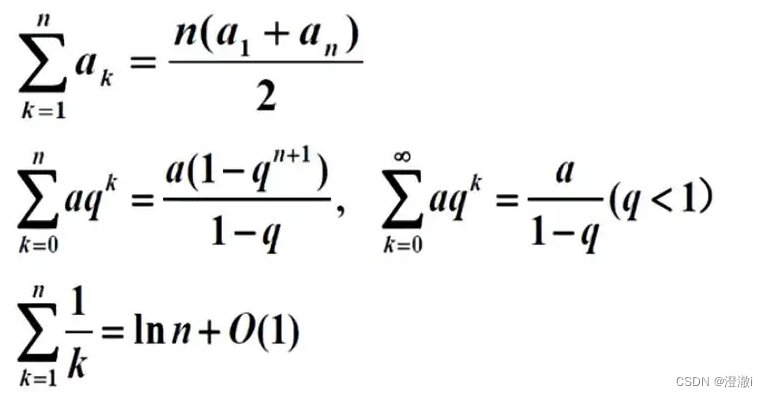
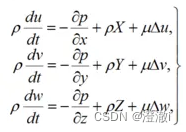
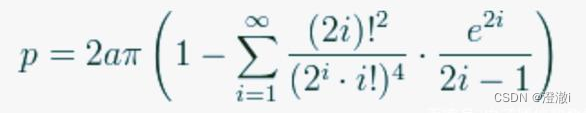
以上复杂公式均采集自互联网。这么复杂的东西,难道我真的要手打吗??!
两种情况:
- 公式定理已经存在且被人拿来使用。这种情况,我们虽然也要打出这个公式,无法粘贴复制,同时也不能直接用图片来作为论文里面的公式。还是逃不了手打的情况,这时候只需要使用
Mathpix Snipping Tool。
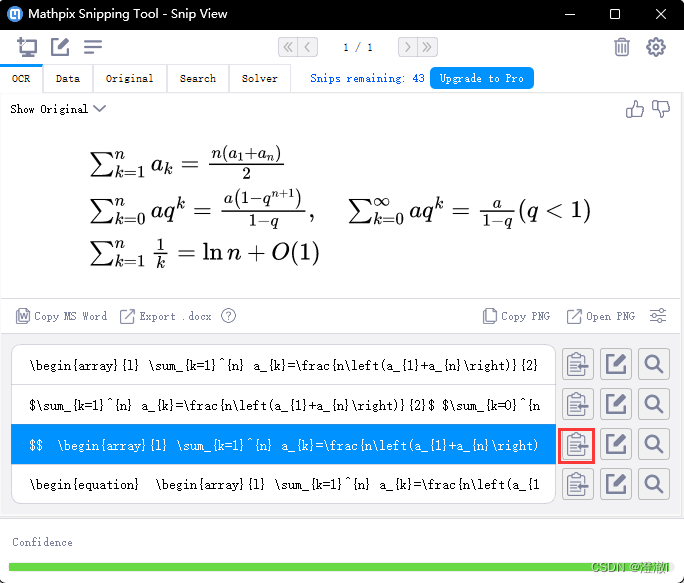
复制后,粘贴即可直接使用。
- 如果实在不会Latex数学公式写法,没事咱就整点易操作的。使用
MathType + Mathpix Snipping Tool
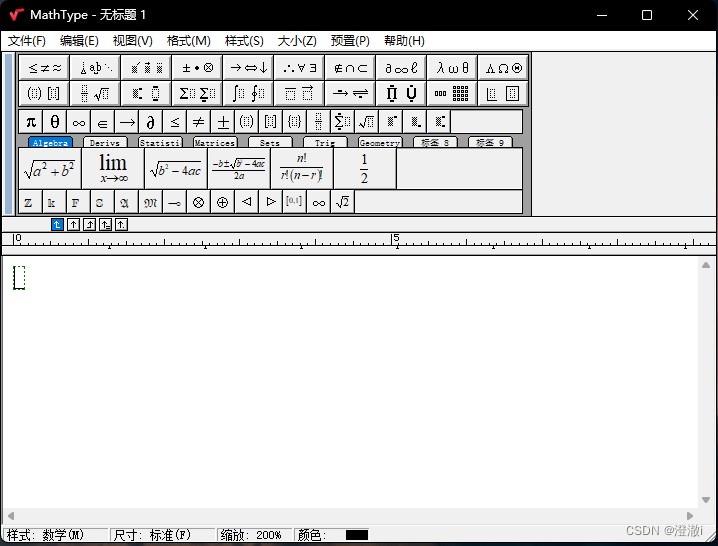
在MathType上使用这种简易化的操作编写公式,再通过刚才方法进行识别。
一些提醒:Mathpix Snipping Tool正版的话是只有50次使用次数,如果平时不怎么使用它来编写Latex公式,最后写论文用一波复杂公式也不失为一个好工具。当然,破解版这东西肯定存在。某宝可以搜搜看。
MathType也有破解版,互联网自取。