一. 隐函数的偏导数
给定隐函数:
隐函数的偏导可得:
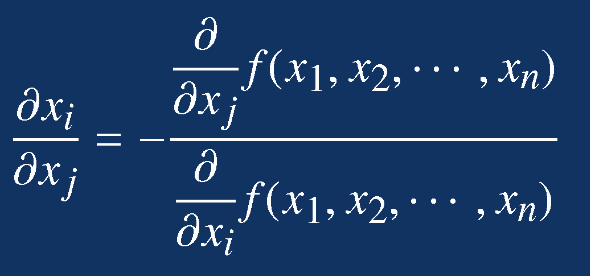
MATLAB格式:
F=-diff(f,xj)/diff(f,xi)例题1
已知:
求:
解:
MATLAB代码:
clc;clear;
syms x y;
f=(x^2-2*x)*exp(-x^2-y^2-x*y);
pretty(-simplify(diff(f,x)/diff(f,y)))运行结果:

二. 不定积分解析解
给出不定积分:
MATLAB格式:
F=int(fun,x)例题2
给定函数f(x),用diff()函数求其一阶导数,再积分,检验是否可以得出一致的结果。
解:
MATLAB代码:
clc;clear;
syms x;
y=sin(x)/(x^2+4*x+3);%一阶导数与积分
y1=diff(y);
y0=int(y1); %对导数积分
pretty(y0)%对原函数求四阶导数,再对结果进行四次积分
y4=diff(y,4);
y00=int(int(int(int(y4))));
pretty(simplify(y00))运行结果:
sin(x)
------------
2
x + 4 x + 3
sin(x)
------------
2
x + 4 x + 3
例题3
证明:

解:
MATLAB代码:
clc;clear;
syms a x;
f=simplify(int(x^3*cos(a*x)^2,x))
f1=x^4/8+(x^3/(4*a)-3*x/(8*a^3))*sin(2*a*x)+...(3*x^2/(8*a^2)-3/(16*a^4))*cos(2*a*x);
simplify(f-f1) %求两个结果的差运行结果:
f =((3*sin(a*x)^2)/8 + (a^3*x^3*sin(2*a*x))/4 - (3*a^2*x^2*(2*sin(a*x)^2 - 1))/8 - (3*a*x*sin(2*a*x))/8)/a^4 + x^4/8
ans =3/(16*a^4)
三. 定积分与无穷积分
给定积分:
MATLAB格式:
I=int(f,x,a,b)给定无穷积分:
MATLAB格式:
I=int(f,x,a,inf)例题4
求当a=0,b=1.5或时的定积分值。
解:
MATLAB代码如下;
clc;clear;
syms x;
I1=int(exp(-x^2/2),x,0,1.5);
vpa(I1,70)
I2=int(exp(-x^2/2),x,0,inf)运行结果:
ans =1.085853317666016569702419076542265042534236293532156326729917229308528
I2 =(2^(1/2)*pi^(1/2))/2
四. 多重积分问题
例题5
求解F(x,y,z)的积分:

解:
积分顺序:
MATLAB代码:
clc;clear;
syms x y z;
f0=-4*z*exp(-x^2*y-z^2)*(cos(x^2*y)-10*cos(x^2*y)*y*x^2+...4*sin(x^2*y)*x^4*y^2+4*cos(x^2*y)*x^4*y^2-sin(x^2*y));%一种积分顺序
f1=int(f0,z);
f1=int(f1,y);
f1=int(f1,x);
f1=simplify(int(f1,x))%换种积分顺序
f2=int(f0,z);
f2=int(f2,x);
f2=int(f2,x);
f2=simplify(int(f2,y))%看两者结果是否一致
simplify(f1-f2)运行结果:
f1 =sin(x^2*y)*exp(- y*x^2 - z^2)
f2 =sin(x^2*y)*exp(- y*x^2 - z^2)
ans =0
例题6
求解如下积分:
解:
MATLAB代码:
clc;clear;
syms x y z;
I=int(int(int(4*x*z*exp(-x^2*y-z^2),x,0,1),y,0,pi),z,0,pi);
%实际上求出来的结果含有Ei(n,z),可求数值解
vpa(I,60)
运行结果:
ans =1.73276222303122046279036924954865797833228791294854004417627