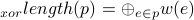好朋友(算法题解)
Description
有一个叫做“数码世界”奇异空间,在数码世界里生活着许许多多的数码宝贝,其中有些数码宝贝之间可能是好朋友,并且数码宝贝世界有两条不成文的规定:
第一,数码宝贝A和数码宝贝B是好朋友等价于数码宝贝B与数码宝贝A是好朋友
第二,如果数码宝贝A和数码宝贝C是好朋友,而数码宝贝B和数码宝贝C也是好朋友,那么A和B也是好朋友
现在给出这些数码宝贝中所有好朋友的信息问:可以把这些数码宝贝分成多少组,满足每组中的任意两个数码宝贝都是好朋友,而且任意两组之间的数码宝贝都不是好朋友

Input
输入的第一行有两个正整数n(n <= 100)和m(m <= 100),分别表示数码宝贝的个数和好朋友的组数,其中数码宝贝编号为1~n。
Output
输出一个整数,表示这些数码宝贝可以分成的组数
Sample Input
7 5
1 2
2 3
3 1
1 4
5 6
Sample Output
3
题解
dfs
这道题是在刷题的时候遇到的,一开始我的思路直接就是建图,然后dfs遍历,每一次遍历都会遍历整个连通分量,然后统计连通分量的个数即可。
并查集
后来发现这道题的普遍解法是并查集的做法,输入一个就找到祖先并且并入,最后统计祖先的个数即可找到相应有多少个连通分量
并查集代码
#include <iostream>
using namespace std;const int N = 110;
int f[N];//找到祖先并进行路径压缩
int getFather(int v){if(f[v] == v) return v;f[v] = getFather(f[v]);return f[v];
}//合并
void merge(int v,int u){int t1 = getFather(v);int t2 = getFather(u);if(t1 != t2){f[t2] = t1;}
}//初始化
void init(){for(int i = 0;i < N;i ++){f[i] = i;}
} int main()
{init();int n,m;cin >> n >> m;int v,u;while(m --){cin >> v >> u;merge(v,u);}int cnt = 0;for(int i = 1;i <= n;i ++)if(f[i] == i) cnt ++;cout << cnt << endl;return 0;
}